下一代移动通信系统高速并行Turbo译码研究与FPGA实现
2008-04-03
作者:陈俊霖, 朱光喜
摘 要: 在深入研究Turbo译码算法" title="译码算法">译码算法的基础上,重点分析了Log-MAP算法,并针对下一代移动通信系统" title="移动通信系统">移动通信系统B3G(Beyond 3G)数据业务高传输速率" title="传输速率">传输速率的要求,提出了一种高效的基于Log-MAP译码算法的FPGA并行实现方法,并利用Xilinx公司的FPGA芯片并行实现100Mbps的译码。实验表明,对B3G系统中高速数据进行译码时,具有较好的误码性能和较理想的译码时延" title="时延">时延。
关键词: Log-MAP算法 下一代移动通信系统 FPGA实现 100Mbps并行译码
Turbo码[1]自1993年提出以来,由于其接近Shannon极限的优异性能,被广泛应用于无线通信系统中,已被确定为第三代移动通信系统的信道编译码方案之一。在下一代移动通信系统中,要求更高的传输速率和更好的误码性能,对信道编译码的要求也相应提高。然而,由于Turbo码迭代译码算法的限制,使得译码复杂度和译码时延成为硬件实现" title="硬件实现">硬件实现的重要问题,性能和资源上的折衷考虑是实现Turbo码的关键。本文对Turbo码进行了深入的研究,提出了适合于FPGA实现的改进的Log-MAP[2]算法,并采用Xilinx公司的XC2VP70芯片实现了译码功能,该译码模块用于B3G系统上行链路。实验表明,在高速率传输下译码的误码率以及译码输出时延能满足B3G业务要求。
1 Log-MAP算法
从Turbo码的提出至今,其译码算法目前主要有最大后验概率(MAP)算法和软输出维特比译码算法(SOVA)算法[3]。SOVA算法运算量最小,较适合硬件实现,但性能较差。目前而言,MAP算法被认为是最佳的译码算法,但是由于其包含大量的乘法和指数运算,不利于硬件实现。在此基础上简化而来的是Max-Log-MAP[4]算法:
ln(ex+ey)≈MAX(x,y) (1)
Max-Log-MAP算法将MAP算法转移到对数域中可以大大降低计算量:在对数域中,不再需要指数运算,原来的乘法转变成加法。然而,这种近似却引来了一定的性能损失。文献[2]中的实验表明,Max-Log-MAP算法相对于MAP算法有0.5dB的损失。实际上,根据Jacobian展开式,ln(ex+ey)≈MAX(x,y)+ln(1+e-|x-y|),就是Log-MAP算法。可以看到,Log-MAP算法仅仅是将MAP算法转换到对数域中进行运算,因此其性能相对于MAP算法是一致的。然而在Log-MAP算法中,对数和指数运算仍然存在,这对于硬件实现还是不利的。文献[2]提出将Log-MAP算法中的加项利用查找表的方法来实现,以减小运算复杂度,同时改善(1)式的性能,即:
ln(ex+ey)≈MAX(x,y)+f(x,y) (2)
=MAX*(x,y)
其中,f(x,y)是关于x-y的分段函数。
下面简要介绍一下Log-MAP算法,其中各分量均为对数域表示。
通过迭代运算,对最后一次迭代得到的LLR进行硬判决,可以得到译码输出的结果。
2 译码器硬件实现时的改进
从式(6)、(7)中可以看到每次迭代时都需要先计算LLR,再通过LLR来计算下一次迭代时需要的外信息Le。但是LLR实际上在最后判决时才会用到,而对于每一级迭代而言,外信息Le才是最关心的。于是,将上面算法作一改进,让系统在每次迭代时仅计算Le,直到判决时再计算LLR,以减少运算复杂度。推导可知:
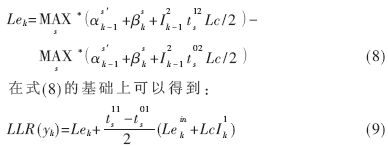
通过以上改进,使得在迭代过程中不依赖于LLR,既减少了计算量,又减少了计算过程中存储LLR所需要的RAM空间。
从式(8)看到,对于整个Log-MAP译码算法而言,由于后向迭代,需要大量的RAM来存储已经计算得到的前向状态度量α。对于码长为L具有N状态的Turbo码,假设每个状态度量用K比特量化,那么存储所需的空间则为L×N×K。同时,每次迭代的输出时延随着码长L增长。这对于硬件实现而言是不可取的,于是采用了文献[4][5]提出的滑动窗技术:对所有状态度量的初始值设为某一任意值,根据网格收敛原理,可认为递归运算一定步数得到的状态度量值是可靠的。假设滑动窗口长度为l,则存储α所需的空间变为l×N×K,由于l=L,可见滑动窗大大减少了存储空间,缩短了每次迭代的输出时延。对于β而言,设窗口总数为M,窗口编号为i,则β变为:
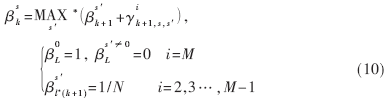
滑动窗的使用在一定程度上影响了系统性能,但是对于FPGA实现而言这是必要的,并且正因为滑动窗计数减少的存储空间,于是可以同时将N个状态度量并行计算且相应存储。
3 译码器的硬件实现方案
根据前面针对硬件实现所改进的Log-MAP算法,译码器的硬件实现如图1所示。
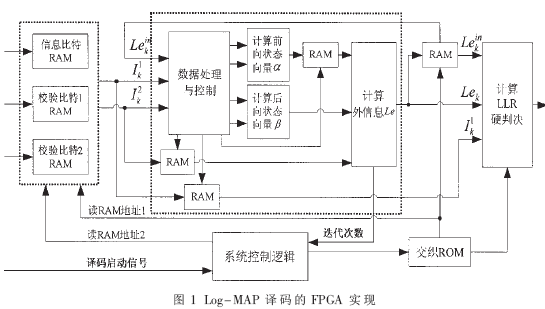
图1中部虚线框图所示即为一次Log-MAP译码操作,可以看到其中由于计算状态度量以及外信息时所需的输入信号在时间上是不同的,于是需要有相应的存储空间存储这些信息,使进入各模块的数据时间上一致。图1中的数据处理与控制模块完成了以上的功能,为计算前、后向状态度量以及外信息提供了时序上的保证。
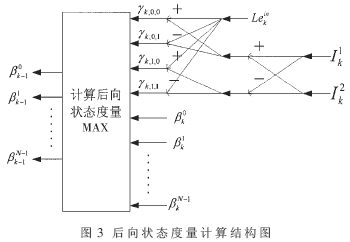
3.1 分支度量计算
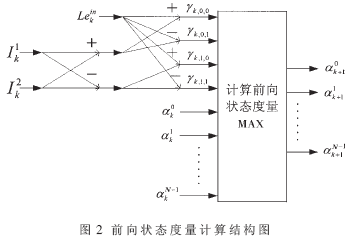
由式(4)、式(5)以及根据第2节中的分析,图2、图3分别给出了并行计算[6] 前向、后向状态度量的结构图。从式(3)计算分支度量γ可以看到,每次迭代时的值只与输入的信息比特和校验比特有关,且对应每个输入信息的分支度量γ只有4种可能,于是本应计算2N个分支度量被减少到4次,大大减少了RAM空间。在图2和图3中,根据式(4)和式(10),选择相应的分支度量和状态度量进行求和操作并取最大值,得到下一组状态度量。其中,由于FPGA实现时受到量化位数的限制,需要对每次迭代后输出的状态度量进行判决,一旦超出量化后可以表示的最大数,则需要对该次迭代输出的N个状态度量减去某一常数,进行归一化处理。
3.2 前后向状态度量的计算
从式(4)和式(10)中可以看到,前、后向状态度量在计算时需要利用上一次计算得到的结果作为下一次迭代的输入,如果数据流不断地输入,即每个时钟对应一个输入数据,则这种迭代运算无法进行流水线计算,一旦运算复杂度过大,必然造成在一个时钟内不能完成运算的现象。由式(3),计算分支度量需要2次加(减)法运算;计算状态度量时,该时刻的状态度量与分支度量相加需要1次加法运算,并且根据式(2),对结果进行修正,又需要1次加法,此外如果数据溢出则还需要1次减法归一化操作。由上面分析可见,在一个时钟里需要2次加法运算来计算分支度量,同时1个时钟里还需要2~3次加(减)法运算来计算状态度量。
对于高速率、高性能译码而言,系统时钟频率相当高,且加(减)法的位数也比较大,要在一个时钟里完成上述操作是不可能的。反之,如果将每次加法都用寄存器型的变量来运算,即每个时钟周期只完成一次加法运算,使用2~3个时钟周期完成一次计算,这样局部实现加法流水线操作,更容易使FPGA运算满足时钟约束。但是,从前面的分析可以看到,迭代运算使得数据流的连续性在这种流水加法时必然造成加法的错位。
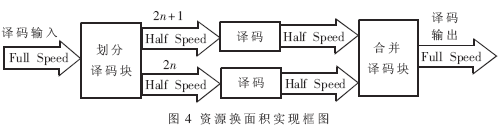
为了解决上述两个矛盾,输入数据就不能按照每个时钟进行输入,而必须降低输入数据的频率。假设在a(a≤3)个时钟周期内完成一次迭代运算,于是输入数据的频率也必须为原始频率的1/a。这样,为了整体上达到系统速率,就需要a个同样的模块并行运算,即利用FPGA资源来换取速度。为保证译码速度,只能牺牲面积来实现上述的复杂加法运算。另外从分析可知,计算前、后向状态度量时最多需要3次加法操作,而一般情况仅需要2次加法运算,折衷面积和速度,选用2个时钟完成一次迭代运算较为理想。这样,利用了双倍的资源,实现了高时钟频率的运算。图4给出了实现框图,其中n为输入译码块的序号。
4 仿真与测试
为了满足B3G系统中对数据业务高传输速率、高性能的要求,对Turbo码的码长、码状态数以及迭代次数都有较高的要求。折衷性能和实现代价,在系统实现中采用了4 416的编码长度,编码器约束长度为4,编码器码率为1/3,5次迭代译码。
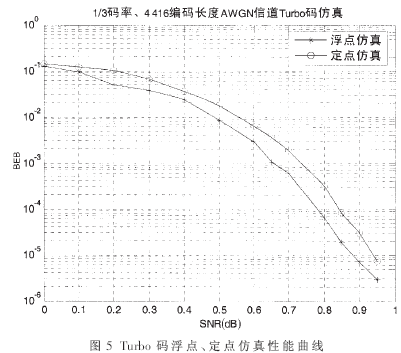
首先在系统仿真平台SPW下完成系统浮点仿真,并采用适当的量化方法以及第3节中提到的硬件实现改进方法对系统进行定点仿真。其中信源由随机数产生,并对其进行QPSK调制。整个系统在AWGN信道下进行仿真测试,图5给出了浮点仿真和定点仿真的性能曲线。从图中可以看到,定点化后的性能和浮点仿真有0.1dB左右的衰减,但在0.95dB左右其误码率已达到10-6 数量级,满足了B3G系统对于信道编译码的性能要求。
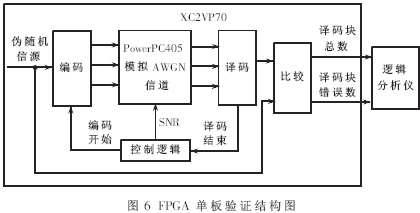
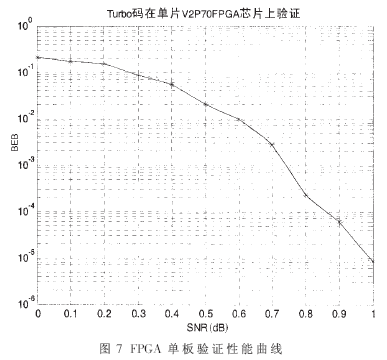
其次采用Xilinx公司的XC2VP70芯片对FPGA实现单个Turbo译码进行了验证。对于少量的译码块,采用与SPW平台仿真对比的方法进行验证。对于连续大量的译码块,采用Xilinx公司Virtex2系列芯片内嵌的CPU核PowerPC405进行辅助测试。利用FPGA实现编码和译码功能,通过PowerPC405核模拟一个AWGN信道将编译码模块相连接,构成一个片上系统,在单板上实现Turbo编译码系统的验证。图6给出了单板验证的框图,图7是该单板系统下仿真曲线。
最后,在上一步测试的基础上,使用4片XC2VP70芯片实现B3G系统的信道译码运算。其中系统时钟频率为100MHz,进入整个Turbo译码系统的数据速率为100Mbps,在整个B3G系统上行全链路状态下完成测试。表1给出了每片FPGA的资源使用状况。

本文深入研究了Turbo码的Log-MAP译码算法,对其FPGA实现做了优化和改进,提出了一种高性能、高速率的基于Log-MAP算法的Turbo码硬件译码算法,并利用FPGA予以实现。该改进的实现算法在保证系统低误码率和短输出时延的情况下,提高了译码速率、降低了运算复杂度、减少系统消耗资源。实验表明,该算法实现的Turbo译码在B3G系统中具有良好的性能,对于实现其他速率的Turbo译码也具有一定的参考价值。
参考文献
1 Berrou C, Glavieux A, and Thitimajshima P.Near shannon limit error-correcting coding and decoding: turbo codes. In: Proc of ICC′93:1064~1070
2 Robertson P, Villebrun E, Hoeher P. A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain. Communications,1995;ICC 95 Seattle,1009~1013
3 Hagenauer J, Hoeher P. A viterbi algorithm with soft decision outputs and its applications. 10.1109/GLOCOM: 1680~1686
4 Viterbi A J. An intuitive justification and a simplified implementation of the MAP decoder for convolutional codes. IEEE Select. Areas in Commun, 1998;16(2):260~264
5 徐韦峰,秦东,李志勇.滑动窗在Turbo码解码系统中的应用及改进. 电子学报,2000;(9)
6 Thul, M.J., Wehn, N. FPGA implementation of parallel turbo-decoders. Integrated Circuits and Systems Design, In:SBCCI 2004. 17th Symposium on 7-11 Sept.2004:198~203

