改进的Snake算法在虹膜定位中的应用
2008-04-10
作者:王 畅,李 峰,成 培,熊
摘 要: 传统的Snake模型在图像边缘检测时定位、分割的结果依赖于初始节点的选取,当初始轮廓线超出图像边界时,会导致分割定位失败。针对该问题,对Snake算法进行改进,详细介绍了改进算法的原理和实现,并用遗传算法" title="遗传算法">遗传算法对结果进行优化。
关键词: Snake模型 虹膜定位 能量函数" title="能量函数">能量函数 区域信息 遗传算法
1 研究现状
虹膜识别" title="虹膜识别">虹膜识别是近几年发展起来的新兴生物特征识别技术。由于虹膜是内部器官,受外界的影响小而且不易改变。与生活中的钥匙和密码相比,人的虹膜不易被修改和盗用。虹膜图像的采集是非接触式的,具有极高的应用性。虹膜定位就是虹膜内外边缘的定位,是虹膜识别技术的关键环节。精确定位是有效进行虹膜识别的前提。传统的定位方法大部分采用Hough变换和Daugman的圆形检测算子。前者需要在参数空间内对三个参数(圆心坐标和半径)进行搜索,计算量和存储量较大,后者虽然速度快,但前提条件是用一个稳健的方法来确定瞳孔的圆心。
Kass等人1988年提出了一种基于能量函数的主动轮廓线(Active contour models)的Snake算法[1~2],并已经证明是一种高效的轮廓探测法[4],但传统的Snake模型存在着许多不足:(1)不能依据图像的目标形态自动分配蛇点;(2)定位、分割的结果依赖于初始节点;(3)容易受局部噪声的影响收敛于局部噪声极值点;(4)弱边界图像求解效果较差;(5)初始轮廓线若超出图像边界时,分割定位会失败;(6)收敛的速度还不够快等。针对这些缺点,本文提出了一系列改进方法来重新构造Snake模型,研究能量函数的构造和蛇点的自适应分布,在定位结束后引入遗传算法优化所得结果。
2 Snake原始模型
传统的Snake模型实际上是一条参数化的样条曲线,设v(s)=[x(s),y(s)],其中s是曲线的弧长,其范围为s∈[0,1],Snake模型[3~5]的能量函数为:
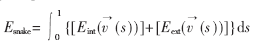
其中Eint(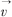 (s)),Eext(
(s)),Eext(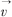 (s))分别为内部能量和外部能量。内部能量函数Eint(
(s))分别为内部能量和外部能量。内部能量函数Eint(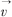 (s))能保持样条曲线的弹性和光滑。外部能量函数Eext(
(s))能保持样条曲线的弹性和光滑。外部能量函数Eext(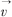 (s))主要决定轮廓收敛于图像特征点。
(s))主要决定轮廓收敛于图像特征点。
3 对Snake模型的改进
3.1 内部能量函数的改进
改进后的内部能量函数为:

式中Ed为目标中心点对蛇点的拉动能量;Ec为轮廓的二阶导数; K为常量;vi-1、vi、vi+1为3个相邻的蛇点;pc为蛇点估计的形心;α、β为能量函数的权值" title="权值">权值。
函数的优点是间接扩大了蛇点的搜索范围,第一个形心由人为选定,在以后的每次迭代中,都由蛇点来估计新的形心。在蛇点运动的起始阶段,也就是刚开始的第10~15次迭代过程中,由于蛇点的起始位置与目标的实际轮廓相差很大,此时用蛇点对形心的估计往往误差较大,可以保持形心的起始位置不变,在经过一段时间的迭代之后,各蛇点的轮廓开始逼近目标轮廓,此时形心将随着蛇点的分布而运动,运动方式为:

其中,vi为蛇点的位置,为了防止形心越界,在运动时,形心将要受到边缘梯度力的控制,满足:
Ecp=max(mEcd+n/Ecg)
式中,Ecp为形心的能量,Ecd为蛇点对形心的拉动能量,Ecg为形心的梯度能量,m、n为系数。
3.2 离散化Snake模型
把结合贪婪算法的Snake模型离散化,表示为:
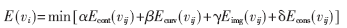
式中i=0,1,…N-1,vi为Snake上的控制点,简称“蛇点”,N为蛇点的总数目,vij为蛇点及其8邻域的点。Econt(vij)、Ecurv(vij)、Eimg(vij)、Econs(vij)分别为对应点的连续性能量、弯曲性能量、图像能量和约束能量,前两项属于内部能量,后两项属于外部能量。α、β、γ、δ分别为各能量项的权值,用以调节各能量项在总能量中的比重,为了平衡各项的影响,各能量项全都归一化为区间[0,1]内的数。
连续性能量采用如下形式:

式中I(vi,j)为点vi,j处的灰度值,minGray和maxGray分别为8邻域内的最小灰度值和最大灰度值。
本文的约束能量采用蛇点到Snake形心的距离势能,采用如下形式:

3.3 引入区域信息来构造图像力
在进行虹膜边界定位时,由于虹膜不具有强边界,有时在获取虹膜图像时带有很强的噪音,传统的Snake模型在处理虹膜图像时,仅使用边界信息,容易使曲线陷入局部最优,本文引入一个区域信息[5]来改善该问题。
取得初始曲线V(0)所包括的区域 统计特征,
统计特征, 的冲击特征可以近似看作待分割目标的统计特征,记为{SF0,j|1≤j≤m},其中m表示区域统计特征的个数,SF0,1是该区域内像素的灰度均值,SF0,2是该区域内像素的灰度方差。取得
的冲击特征可以近似看作待分割目标的统计特征,记为{SF0,j|1≤j≤m},其中m表示区域统计特征的个数,SF0,1是该区域内像素的灰度均值,SF0,2是该区域内像素的灰度方差。取得 的特征后,考察V(t)上的点Vi为中心,K×K区域的特征,一般取K=3。计算统计特征{SFi,j|1≤j≤m},得到该区域和
的特征后,考察V(t)上的点Vi为中心,K×K区域的特征,一般取K=3。计算统计特征{SFi,j|1≤j≤m},得到该区域和 的统计相似度:
的统计相似度:
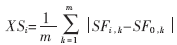
其中m表示统计特征个数,SFi,k为Vi所在区域的统计特征,SF0,k为?覣0的统计特征,在得到两者的相似度后,可以定义图像力为:
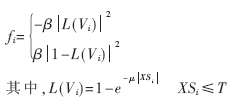
式中μ为正数,0≤μ≤1。当XSi≤T时(T为阈值),说明Vi所在的区域可以近似看作目标内部区域,此时曲线继续沿外法线方向运动(膨胀);相反XSi≥T时,说明Vi所在的区域可以近似看作背景区域,曲线沿内法线方向运动(收缩)。
4 实验结果
本文采用CASIA虹膜图像数据库(版本1.0) ,其中包括80人(男62人,女18人)108只不同眼睛的虹膜图像样本,每只眼睛有7幅8位灰度图像,分辨率为320×280。
选取一幅虹膜图像,Snake模型的具体参数设置为:初始节点选取15个,连续性能量函数系数为α=1.0,弯曲性能量函数系数为β=0.5,图像能量函数系数为γ=1,约束能量函数系数为δ=-7.0,阈值T=97,遗传算法[6]的种群染色体数目为M=50,交叉概率为Pc=0.24,变异概率为Pm=0.02,迭代次数为R′=60。
由于虹膜外边界上眼睑的睫毛噪音难以消除,作者采用先定位虹膜内边界,得到形心的位置后,以瞳孔的半径为虹膜外边界的初始半径,使用简化的Daugman算法定位下半个虹膜轮廓,然后镜像出整个虹膜外边界。
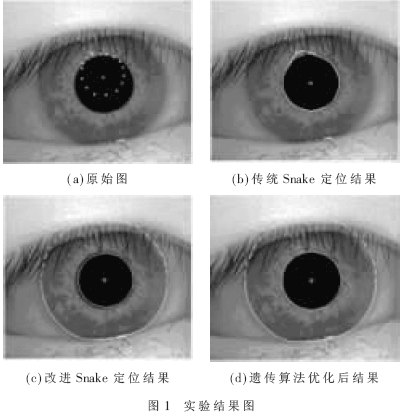
实验结果如图1所示。其中,图1(a)为初始曲线的位置,为了证明本文方法的优点和稳定性,因此本文在选取初始点时使初始点没有完全位于虹膜内边界的内部。图1(b)为传统Snake模型基于边界信息的外力定位的结果,根据此图可以看到,在传统Snake模型的定位下,若初始节点超出目标边界,则最后定位的曲线会超出边界的区域,不能再缩回到正确的边界位置,并受到噪声的影响,导致定位失败。图1(c)是改进后的Snake模型基于区域信息的定位结果,即使初始节点位于目标轮廓的外部,仍能受到外力的拉伸,渐渐向真实的边界靠拢,达到较优的定位效果。图1(d)是使用遗传算法对改进后Snake模型的求解进行优化的结果。可以看出,优化后的曲线更加趋近于虹膜边界,而且更加光滑,效果更好。
图中的“十”字形交点为形心,在定位时间上与其他算法比较如表1所示,原始Snake模型定位失败,定位的结果并没有真实反应虹膜内边界的轮廓,改进后的Snake算法耗时最少,精度较高。由于有部分初始点落在虹膜内边界以外,因此耗费的时间并没有体现出很明显的优势。

本文就改进的Snake模型在虹膜边缘定位中的应用进行了分析,改进了Snake模型的内部能量函数,并结合贪婪算法对Snake模型进行离散化;然后引入区域信息来构造图像力,使得改进后的Snake模型减小了噪音的干扰;最后,使用遗传算法对Snake模型的求解进行优化。实验结果证明,上述算法与传统的Snake模型算法相比,具有更好的定位效果,定位出来的虹膜内边界更加光滑,并且接近虹膜边界,鲁棒性更强。此方法也适用于连续图像的分割及追踪,对凹凸性变化较强烈的图形也有很好的分割效果,作者将对此做更进一步的研究。
参考文献
1 Kass M,Witkin M,Terzopoulos D.Snakes:Active contour models[J].International Journal of Computer Vision,1987;1(4):321~331
2 Cohen L D,Cohen I.Finite-element methods for active contour models and balloons for 2D and 3D images[J].Pattern Analysis and Machine Intelligence,1993;15(11):1131~1147
3 赵保军,李 栋.对复杂边缘检测的Snake改进算法[J].北京理工大学学报,2004;24(2):162~165
4 苑玮琦,马军防,狄文彬.基于主动轮廓线的虹膜定位算法[J].计算机工程与应用,2003;40(34):104~107
5 陈允杰,张建伟.一种新的图像力在Snake模型中的应用[J].计算机应用" title="计算机应用">计算机应用,2004;24(12):28~30
6 陈允杰,张建伟.遗传算法在Snake模型中的应用[J].计算机应用,2004;24(5):80~84

