近年来，应用摄像机等视觉传感器及计算机视觉" title="计算机视觉">计算机视觉理论对车辆进行识别与跟踪在城市交通监控中有较大的发展。它涉及到视频信号的采集、视频信息的处理与分析、计算机人工智能等。其中交通信息的采集与分析是最基础，也是最重要的环节，需要根据图像中的二维信息来提取实际空间中的三维信息。许多文献中都提到了采用摄像机标定" title="摄像机标定">摄像机标定来完成从二维到三维的转换^[1～2]，但传统的标定算法都需要一个高精度的模板和不同角度的图像。利用模板的精确数据" title="精确数据">精确数据与其图像数据进行匹配来求得摄像机内外参数的方法有较大的局限性。有些采用双目方法来恢复三维信息^[3～4]，但需要在两幅图像之间进行相关匹配。如果同一幅图像上有多处极为相似，则容易出现匹配错误，且该算法的耗时会影响监控的实时性。本文提出了一种基于图像网格的形变校正算法，由此计算单应性矩阵，无需用到标定块，从而实现在单目图像序列中提取车辆三维信息。该方法在智能交通系统ITS（Intelligent Traffic System）中有较好的应用。
1 系统概述
　　本系统的信息流程图如图1所示。将由二维图像获取的信息，通过网格非线性校正算法计算从图像平面到空间平面的变换系数，即二维单应性矩阵，由此进行对摄像机参数的标定，由内外参数矩阵确定三维单应性矩阵，即确定从二维图像恢复到实际三维信息的变换关系。

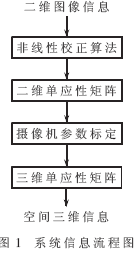
2 摄像机成像几何模型
　　假定摄像机的成像模型为经典的小孔成像模型^[5]，即只考虑线性模型，暂不考虑透镜引起的畸变，具体的几何模型如图2所示。

　　由摄像机的光轴" title="光轴">光轴与图像平面组成的直角坐标系称为摄像机坐标系。如图2中的O-XcYcZc为摄像机坐标系，O为光学中心，Zc轴与光轴重合，O₁-xy为图像平面坐标系（坐标原点在图像中心），O₂-uv为以像素点为单位的图像平面坐标系。在O-XcYcZc坐标系下，O₁点的坐标为(0，0，f)，f为摄像机的焦距，同时在O₂-uv坐标系下O₁点的坐标为(u₀，v₀)。
　　设空间一点P在摄像机坐标系下的坐标为(XcYcZc)，通过透视投影而在成像平面上生成的对应像点的像素坐标为P′(u，v)，两者之间的比例关系用齐次坐标表示为：
　　
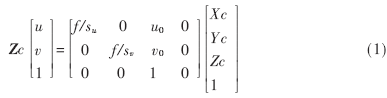
　　式中的s_u、s_v分别为像素的宽度和高度，f、u₀、v₀、s_u、s_v称为摄像机的内参数。
　　由于摄像机可以安放在环境中的任何位置，所以应在环境中选择一个基准坐标系来描述摄像机的位置，该坐标系称为世界坐标系。摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵R和平移向量μ来描述，因此空间点P在世界坐标系与摄像机坐标系下的齐次坐标之间有如下关系：
　　
　　其中，(X，Y，Z)为点P的世界坐标，R为3×3单位矩阵，μ为三维平移向量，O^T=(0，0，0)。
　　由式(1)、(2)可得点P的世界坐标与投影点P′的像素坐标之间的关系：
　　
　　M₁只与摄像机的内参数有关，称为内参数矩阵，M₂与摄像机的外参数有关，称为外参数矩阵，则式(3)可表示为：
　　
　　由上式可知，只要标定了摄像机的内外参数后，即可建立图像点的像素坐标与实际点的世界坐标之间的关系。
　　将外参数矩阵中的旋转向量R表示为：
　　R=[r₁，r₂，r₃]
　　其中r₁，r₂，r₃均是3×1的矩阵，则可将式(4)表示为：
　　
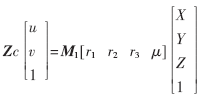
　　在不失问题一般性的情况下，先假设标定物体位于世界坐标系中Z=0的平面内，则上式简化为：
　　
　　传统的标定方法中，在实际场景中设定一个高精度的标定块，利用标定块上点的精确数据与其图像中的数据进行匹配，得到单应性矩阵H。本系统中的单应性矩阵H由基于网格的非线性校正算法求得。
3 基于网格的非线性校正算法
　　在所摄取的图像上建立坐标系，规定图像的左上角顶点为坐标原点，如图3所示。根据道路的交通标志" title="交通标志">交通标志线设定图像中的网格线，对应到实际道路中的网格线和坐标系，如图4所示。通过在图像上取点获取像素坐标可以计算出图像网格中每条直线的方程，从而可得到各直线的交点坐标。在实际道路中由道路的宽度和交通标志线来确定实际道路网格的交点坐标。这两类交点坐标之间有一一对应的关系，根据这些点坐标的对应，可以找到一个函数关系来反映图像中所有点的坐标到实际坐标的映射。

　　由于图像上不同位置的点发生非线性形变的程度不同，如果所有的点都对应同一个映射关系，则不能保证校正的准确性。为了使坐标的变换更为准确，可以在图像上和实际道路中建立小网格模型。在图像中的每个网格上取若干个点，分别对应到实际网格的若干个点上，由这些点的坐标对应关系建立每个网格的坐标映射函数。在本算法中，将各网格分成9个小格，取其边界和中心的16个点进行映射。这样，在进行非线性坐标变换时，首先判断被计算点所处的网格位置，再选择相对应的映射函数进行变换。
　　由于精确的函数难以求得，故采用近似的方法尽可能地逼近所求函数。在此校正算法中，采用最小二乘法^[6]的曲线进行拟合。这里取基底函数Φ=Span{X，Y，1}，所求的逼近函数用矩阵表示为：
　　

　　
　　其中m为网格中的交点数，交点数越多拟合得越精确。
4 摄像机参数的确定
　　在上面的算法中已经得到二维单应性矩阵，其中旋转矩阵的各旋转分量互相正交^[7]，所以r₁×r₂=0，于是可得到：

　　要求得摄像机的内参数首先需要确定B的6个变量。对于确定的摄像机，分辨率是已知的，所以成像中心的像素值(u₀，v₀)可以得到。将矢量b表示为：
　　
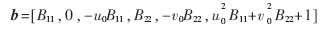
　　所以只要确定两个未知量就行了。将矩阵H的第i列矢量表示为：

　　其中v_ij为6×1矩阵，各元素由已经求得的单应性矩阵的元素决定：
　　
　　于是就完成了摄像机参数的标定，确定了三维单应性矩阵，实现由二维信息到三维信息的变换。
5 实验结果及在视频监控中的应用
　　为了验证上述算法的有效性，将其应用于交通视频监控系统中，以准确提取车辆信息。以上海某外环高架路段为测试对象，测试时间为2005年7月26日下午2：20～2：40，所用摄像机分辨率为1024×768。由本算法计算得到的内外参数分别如表1、表2所示。其中，f_u、f_v分别为摄像机在横向与纵向上的焦距，(u₀，v₀)为成像中心点的像素坐标，r₁，r₂，r₃为摄像机外参数中的旋转向量，μ为外参数中的平移向量。

　　由此对进入系统所设定的检测区域内的车辆计算三维信息，在后续帧中根据这些信息对车辆进行识别与跟踪。部分跟踪效果如图5所示（对尚未进入或已经出了检测区域的车辆不进行跟踪）。