数字电路中△I噪声的危害
2008-04-15
作者:周胜海, 刘百超
摘 要: 为适应数字电子系统的发展需要,研究数字电路" title="数字电路">数字电路中△I噪声的特性和抑制△I噪声的技术变得越来越重要。在△I噪声的产生过程及其基本特点的基础上,研究了△I噪声的主要危害。结果表明,△I噪声主要引起数字系统" title="数字系统">数字系统的电源电压" title="电源电压">电源电压波动、电路内部噪声、输出波形畸变和传播延迟、功耗增加、辐射发射等问题。
关键词: △I噪声 电源波动 地线噪声 功耗增加 辐射发射
随着数字电路向高集成度、高性能、高速度、低工作电压、低功耗等方向发展,数字电路中的△I噪声的特性和抑制△I噪声的技术成为一个亟待系统、深入研究的领域。
△I噪声的产生过程及其基本特点表明[1,2]:△I噪声是由数字电路的电路结构和工作过程决定的,恰当的电路设计只能在一定程度上减小(而不可能消除)△I噪声。△I噪声是数字电路固有的。数字电路中不同单元产生的△I噪声会发生叠加,电路的规模越大,叠加出现的可能性越大,造成的电流尖峰脉冲越强;△I噪声是宽带噪声源,频谱宽度主要由电路的速度决定,速度越高,频谱范围越宽;△I噪声同时产生传导骚扰和辐射骚扰,电路的速度越高,辐射发射越强。
本文在△I噪声的产生过程及其基本特点的基础上,研究△I噪声的主要危害。
1电源电压波动
1.1寄生电阻引起的电源电压波动
数字IC内部和数字系统中都有电源分配网络。电源分配网络的导线都有寄生电阻。电源电流尖峰脉冲(△I噪声)通过电源分配网络时,会产生欧姆电压降。从而引起电源电压波动。
对数字IC内部的电源分配网络,以目前流行的“Vanilla” 0.25μm CMOS工艺为例,考虑一条长2cm的电源线(VDD)或地线(IC内部互连线),其上每1μm宽度的电流为1mA。这一电流密度接近于一条铝线所能承受电流的最大值,原因是电迁移(electronmigration)的影响[3]。该导线(1μm宽度)的电阻为1kΩ。一个1mA/μm的电流将导致1V的电压降。这一电源电压波动将降低噪声容限,并使电路各点的逻辑电平与离开电源端的距离有关。
如图1所示,把一个离电源引线和地引线都很远的反相器" title="反相器">反相器连接到一个接近电源的器件上。由于电源地线上的电压降IR(欧姆电压降)引起的逻辑电平差可能使晶体管TN部分导通" title="导通">导通,可能引起一个预充电的节点X意外放电。如果连接的门是静态的,则有可能引起静态功耗。
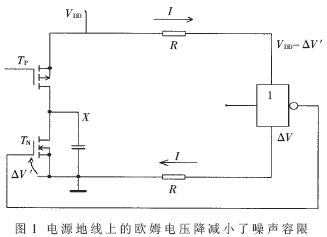
总之,来自片上逻辑电路和存储器及输入/输出(I/O)引线上的电流脉冲会造成电源分配网络上产生电压降,这是片上电源噪声的主要来源。除了造成可靠性降低的风险外,电源网络的欧姆电压降也会影响系统的性能,因为电源电压的一个很小的下降都可能造成延时的明显增加。
无论是数字IC内部的电源分配网络的导线(目前多用铝),还是数字系统中的电源分配网络的导线(一般用铜),都存在趋肤效应(skin effect)。趋肤效应使导线的有效导电截面积随信号频率的升高而减小,使导线的电阻随信号频率的升高而增大(![]() )[4,5]。
)[4,5]。
由于△I噪声是宽带噪声源,所以趋肤效应会使电源分配导线的电阻显著变大(相对于直流电阻),进而使欧姆电压降显著变大。
1.2 寄生电感引起的电源电压波动
电源分配网络还有寄生电感,数字IC的电源地线也有寄生电感。
电源电流尖峰脉冲(△I噪声)通过电感时,会产生感应电压,从而引起电源电压波动。
单个TTL反相器引起的电源电流尖峰脉冲最小值约为30mA[1,2],设门电路的状态转换时间为2ns,设电源地线的寄生电感L=500nH,则引起的电源电压波动为:
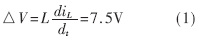
这样高的尖峰脉冲电压通过逻辑器件之间的驱动线耦合到其他逻辑器件的输入端,幅值很可能超过TTL系列输入低电平的上限值0.8V,从而造成逻辑电路的误动作。
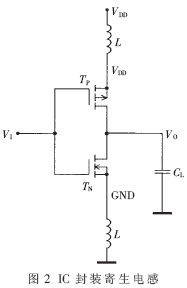
CMOS数字IC中电源电流尖峰脉冲(△I噪声)经封装寄生电感引起的电源电压波动如图2所示。图中电路是数字IC输出压焊块驱动器(output pad driver)的最后一级,它驱动一个10pF的负载电容,电压摆幅(voltage swing)为2.5V。反相器的尺寸设计成使输出信号的上升时间和下降时间(tr和tf)等于1ns。由于电源和接地线是通过电源引线连到外部电源上的,所以两根连线都具有一个寄生串联电感L。对于传统的穿孔(through-hole)封装技术,其电感一般为2.5nH左右。为简化分析,假设反相器的作用像一个电流源,以不变的电流充(放)电负载电容。为达到1ns的输出上升时间和下降时间,所需要的平均电流为:
Iav=[10pF×(0.9-0.1)×2.5V]/1ns=20mA
当这一情形发生在缓冲器输入端并由一个很陡的阶跃函数来驱动时,若tf=50ns,则仿真得到突变的电流变化可在寄生电感上引起高达0.95V的尖峰电压。事实上,如果这一电压降本身不能使翻转变慢和降低对电流的要求,它的值会更大。然而,如此大的电源电压波动是不能允许的。
在一个实际的电路中,单个电源引线常常用于许多门或输出驱动器。这些驱动器同时切换会引起更为严重的瞬态电流和电压降。结果,内部电源电压与外部电源电压有相当大的偏差。例如,如果一条输出总线的16个输出驱动器的电源线都连到同一条封装引线上,则它们同时切换时会引起至少1.1V的电压降。
1.3 电源电压波动与时钟抖动
时钟是数字系统的核心之一。时钟的产生与分布对系统的性能和功耗都有显著影响。时钟偏差(clock skew)和时钟抖动(clock jitter)[6]是主要问题,它们会导致数字系统的性能下降或工作出错。然而,电源电压波动是引起时钟分布网络中抖动的主要原因[7]。
从上述分析可见,△I噪声会引起电源电压波动。电源电压波动造成的不良后果是多方面的、是严重的。考虑到数字电路的规模越来越大及△I噪声的叠加性,这一问题会变得更加严重。
一个数字系统要求对各个门电路提供稳定的电源电压。为了确保正常工作,电源电压的波动应控制在几百毫伏以内。所以,电源电流尖峰脉冲问题,已成为现代数字设计中必须解决的关键问题之一。
2电路内部噪声
在模拟电路中,外界噪声通常是关注的重点。而对于数字电路,则内部噪声最值得关注。一般来说,产生内部噪声源的原因包括地线噪声、电源线噪声、传输线(transimission line)反射、串扰(crosstalk)等,其中最重要的噪声源是地线噪声和电源线噪声。
2.1 地线噪声
由△I噪声产生过程的分析可知,负载电容CL在放电时引起电流尖峰脉冲,该电流尖峰脉冲流经接地线。由于接地线存在寄生电感,所以电流尖峰脉冲流经接地线时,便产生噪声电压,即地线噪声(接地线还有寄生电阻,但相对于寄生电感引起的噪声而言,其引起的噪声要小得多,可以不予考虑)。
实际上,由两个晶体管同时导通引起的电流尖峰脉冲也流经接地线,但由于相对于负载电容CL放电引起的电流尖峰脉冲而言,该电流尖峰脉冲要弱得多,所以在分析电流尖峰脉冲在接地线上引起的噪声时,该电流可以不予考虑。
为方便起见,在具体分析地线噪声的产生与危害时,可将逻辑电路等效为图3所示的形式。
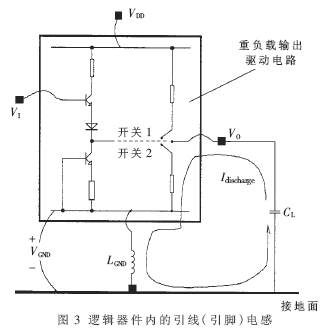
当开关2 接通时,负载电容CL对地放电。随着上电压的下降,其存储的电荷流向地,在接地回路上形成一个电流尖峰脉冲,记作Idischarge。
随着放电电流建立然后衰减,这一电流变化通过接地引脚的电感起作用,在器件外的系统地平面与封装内的地之间感应产生了一个电压VGND,其大小为:

与满幅值的输出电压相比,VGND通常较小。它不会严重影响发送信号,但会严重干扰负载,影响对信号的接收。因为对接收电路而言,VGND脉冲就像是直接叠加在输入信号上的噪声。
以上是TTL电路的情况。虽然CMOS电路的拓扑(topology)结构不同,但噪声脉冲的概念是一样的。
如果同一芯片上的N个容性负载相应的N路输出同时转换,则会得到N倍的地电流,于是噪声脉冲的增大也接近N倍。
地线噪声可能破坏数字系统的正常工作。例如参考文献[4]中所述,一个TTL 八D触发器,由单一时钟输入,驱动一组32个存储器的芯片组。以每条输入线5pF负载电容计算,每条地址线的容性负载为160pF。分析可知,地线噪声可能引起双重触发(误触发)。然而,从外部观测时钟输入,显示的是一个完全干净的信号,错误只出现在器件封装内部。
测试表明,74HC174(四触发器)中单个触发器输出跳变引起噪声脉冲VGND大约为150mV,而在74F174上引起的噪声脉冲VGND是400mV。进一步分析可知,这样大的脉冲足以引起严重问题。
在工程实践中,可用下式估算噪声脉冲VGND的大小:

式中,tr(f)为逻辑器件的上升(或下降)时间(10%~90%转换时间),△V为转换电压。tr(f)和△V的大小取决于逻辑电路系列的性能指标,计算时取典型值。
实际上,这种地线噪声已成为现代数字系统中的主要噪声源之一,其危害往往严重而复杂。除了上面的示例外,边沿触发器的输入线(如复位和中断服务线)也特别容易受到地线噪声的影响。地线噪声引起的EMI辐射已成为一些数字电子产品不能通过相关的EMC强制测试认证的主要原因之一。
2.2 电源线噪声
由于电源分配网络有寄生电感和寄生电阻,因而当△I噪声电流流过时,便产生噪声电压(自感电压和欧姆电压降),即电源线噪声。
对数字IC而言,电源线噪声是电源噪声的主要来源。
电源线噪声会引起电源电压波动。电源电压波动带来的危害在本文的前面已讨论过,故不赘述。
在数字系统中,地线噪声的影响较电源线噪声的影响大。因为电源线噪声可以通过合理使用去耦电容器(decoupling capacitor)予以有效控制,而地线噪声无法通过去耦的方法来解决。
3 输出波形畸变和延时增加
3.1 输出波形畸变
TTL反相器负载电容CL的放电回路的等效电阻Req很小[1,2],这个回路就成为一个高Q值的RLC串联电路,容易产生振荡,引起逻辑门的输出波形畸变(振铃,ringing),甚至使输出电压从正电压变成负电压。实际上,负载电容CL充电时,充电回路也形成一个RLC串联谐振电路,但由于R4相当于串联谐振电路中的一个阻尼电阻(damping resistor),所以该串联谐振电路引起的振铃不严重,通常不予考虑。
振铃幅度足够大时,就会在负载电路(接收端)的输入端产生非法的电平过渡,使传送的信息出错,并可能出现影响逻辑设计的寄生逻辑状态。在有些情况下,振荡幅度可能超过电压的极限值,造成器件损坏[8]。
3.2 延时增加
△I噪声引起电源电压降低。由反相器的电路结构和工作原理可知,电源电压降低使反相器的驱动能力降低,进而使反相器的延时增加。
由于数字电路的输出端一般都有缓冲器,缓冲器与反相器的结构和性能基本相同,所以△I噪声将使数字电路的延时增加。而且,由于△I噪声在电源分配网络的不同位置引起的电源电压下降不同,所以对不同位置的缓冲器造成的延时增加也不同,这将使对数字电路的时序分析变得更加复杂。
4 功耗增加
4.1 TTL反相器功耗增加
根据TTL反相器电源电流尖峰脉冲波形[1,2],可求得电源电流尖峰脉冲引起的功耗增加。在计算时,因输出电平由高向低转换的过程中产生的电源电流尖峰脉冲相对很小,故忽略不计。
为简化计算,可将电流尖峰脉冲近似为三角形脉冲,并认为尖峰电流的持续时间等于传输延迟时间tPHL。如果每个周期中输出高、低电平持续的时间相等,在考虑电源电流尖峰脉冲的影响之后,电源电流的平均值将为:
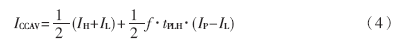
式中,IL为输出为低电平时的电源电流,IH为输出为高电平时的电源电流,IP为电源电流尖峰脉冲的峰值,f为输入信号的频率,tPLL为门电路的传输延迟时间。
式(4)中第2项为电源电流尖峰脉冲引起的电源平均电流增加。
对于TTL反相器,已算出IL≈3.4mA、IH≈1mA和Ip=34.7mA[1,2],并知tPLL=15ns。若输入电压信号为f=5MHz的矩形波,且占空比(duty cycle)为50%,将相关数据代入式(4),可求得此时电源电流的平均值为ICCAV=3.37mA。这个结果比单纯地用IL和IH平均所得到的数值增加了53%。
4.2 CMOS反相器功耗增加
根据CMOS反相器瞬时导通电流的波形[1,2],可求得CMOS反相器瞬时导通电流引起的功耗。
为简化计算,可将电流脉冲近似为三角形脉冲,且认为反相器的上升和下降响应是对称的。在这样的假定下,可求得平均功耗为:
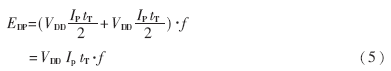
式中,IP为电源电流尖峰脉冲的峰值,tT=t2-t1=t4-t3为TP和TN同时导通的时间,f为输入信号的频率。
根据CMOS反相器对负载电容充、放电电流的波形,可求得iP和iN所产生的平均功耗为[1,2]:
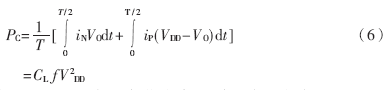
式中, iP、iN分别表示负载电容CL充、放电电流。
CMOS反相器的动态功耗比静态功耗大得多,一般情况下,静态功耗可以不予考虑。
例如,对一个专门的CMOS反相器,VDD=15V,静态电源电流IDD≤1μA,负载电容=60pF。输入信号为理想的矩形波,频率f=100kHz。据式(6)可得PC=CL f V2DD=1.35mW,而静态功耗为PS=IDDVDD=0.015mW,显然,PC>>PS。
值得注意的是,随着数字IC的发展,频率f(工作速度)不断提高。同时,数字IC中门的数目越来越多,芯片上总电容(CL)也在增加。这都将引起功耗进一步增大。
从上述分析可见,△I噪声会引起数字电路的功耗明显增加,且随着数字电路向高速度和大规模方向的不断发展,这一问题会越来越突出,已逐步成为数字设计的关键问题之一。
5 辐射发射
对△I噪声引起的辐射发射,小环天线方式是主要的。
设小环天线的环路面积为A、电流大小为I、电流频率为f,则在距离为r处的自由空间的辐射电场强度为[9,10]:
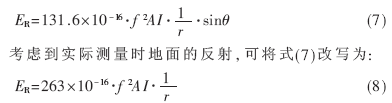
式(8)表明,小型环状天线的辐射强度与电流大小I、电流频率的平方及环路面积A成正比。
由△I噪声的基本特点可知, △I噪声引起的辐射发射十分复杂,与很多具体因素有关,定量计算是很困难的。为了对△I噪声引起的辐射发射的强度有一个定量的概念,作如下分析。
利用式(8)解环路面积A,可得到不超过标准发射限值的最大环路面积。面积A可表示为:

式中, ER表示辐射电场强度(μV/m),r表示环路与测量点的距离(m),f为电流频率(MHz),I为电流大小(mA),A为环路面积(cm2)。
对一个TTL反相器,若取I=35mA,f=30MHz,r=3m,ER=100μV/m,则由式(9)可求得A=3.6cm2。
r=3m时ER=100μV/m是美国FCC(Federal Communications Commission)标准B类产品(住宅应用)所允许的辐射限值。也就是说,当I=35mA、f=30MHz时,若A>3.6cm2,则辐射超标。
若再考虑到△I噪声具有叠加性,以及数字电路的速度越来越高,则△I噪声引起的辐射发射问题更为严重。现在△I噪声引起的辐射发射已成为很多数字系统(电子产品)难以通过EMC强制测试认证的主要原因。
△I噪声主要引起数字系统的电源电压波动、电路内部噪声、输出波形畸变和传播延迟、功耗增加、辐射骚扰等严重问题。这些危害集中体现在两个方面。一方面会导致系统本身性能下降、工作出错甚至完全失效。对系统本身造成的危害一般是多方面的,且往往相互交错。另一方面会导致系统的辐射发射超标。辐射发射超标已成为很多数字系统(电子产品)不能通过EMC强制测试认证的主要原因。
△I噪声的危害,与很多具体因素有关,一些危害相互交错、相互影响,很难对它们进行简单地分类。所以,目前对其建模与仿真尚在研究阶段,是EDA技术中最困难的问题之一。
参考文献
1 周胜海.数字电路中的△I噪声研究[D].武汉:华中科技大学,2005
2 周胜海.数字电路中△I噪声的产生与特点[J].电子技术应用,2006;32(8)
3 J Tao, N Cheung, C Hu. An electromigration failure model for interconnects under pulsed and bidirectional current stressing[J]. IEEE Trans. on Devices, 1994;41(4):539~545
4 Johnson H, Graham M. High-speed digital design: A handbook of black magic[M]. Englewood Cliffs (NJ, USA):Prentice Hall,1993:151~158
5 Hall S H, Hall G W, McCall J A.High-speed digital system design: A handbook of interconnect theory and design practices[M]. New York (NY, USA): John Wiley & Sons, 2000:74~90
6 Young B. Digital signal integrity: Modeling and simulation with interconnects and packages[M]. Englewood Cliffs (NJ, USA): Prentice Hall, 2001:119~121
7 Rabaey J M, Chandrakasan A, Nikolic B. Digital integrated circuits: A design perspective[M]. 2nd edition. Englewood Cliffs (NJ, USA): Prentice Hall, 2003:506~507
8 周胜海,马建中.传输线路引起的数字信号畸变与抑制[J].计算机测量与控制,2002;10(10):695~697
9 Weeks W L. Electromagnetic theory for engineering applications[M]. New York (NY, USA): Wiley, 1964:565
10 Stutzman W L, Thiele G A. Antenna theory and design [M]. New York (NY, USA): Wiley, 1981:99

