一种基于频域分析的MIMO系统盲辨识
2008-04-15
作者：郝东来1，2, 葛建华2
摘 要： 基于高阶" title="高阶">高阶统计量（HOS）的分析方法，针对多输入多输出的MIMO系统中输入多于输出的情况进行了探讨，在对时域中其盲辨识原理进行分析的基础上，提出了一种基于频域" title="频域">频域分析的思路，以3×2 MIMO系统为例，基于互多谱累积量" title="累积量">累积量实现了MIMO系统的盲辨识，并对其实现过程进行了总结和仿真。
关键词： 高阶统计量 MIMO 盲辨识 互多谱
系统盲辨识的目标是通过n个系统输出来辨识系统的传输函数H(z)，通过H(z)估计恢复出系统的r个输入。MIMO系统的盲辨识有着很重要的应用，因为许多问题都可以归结为MIMO盲辨识问题。MIMO系统的辨识是对SIMO方法的扩展。本文提出一种基于频域分析的方法来辨识n×r的MIMO系统，其输入信号" title="输入信号">输入信号为独立同分布的量。通常情况下讨论的MIMO问题都是输出信号的个数n≥r[1]。这种情况下一般经过解卷积来恢复输入信号。在本文中考虑输入多于输出的情况，也就是说n
假定MIMO系统模型为：
x=Hs （1）
其中x=[x1(t)x2(t)]T 为二维输出矢量信号，s=[s1(t)s2(t)s3(t)]T为三维输入信号矢量，si(t)为零均值独立同分布非高斯白噪声，H为2×3维瞬态矩阵。为方便起见，定义以下累积量[2]：
∧为对角阵，ejΦ用来替代每一行的模糊相位。P为行交换矩阵，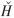
为混合矩阵的估计值，可以通过（9）式得到。这样即可通过（10）式得到H，从而由（1）式估计出输入信号。
2 基于频域实现的MIMO系统的盲辨识
为了更进一步方便对MIMO系统进行盲辨识，将（1）式进行傅立叶变换得到（11）式：
X(ω)=H(ω)S(ω) (11)
可以通过估计xi(ω1)、xj(ω2)……的互累计量谱得到输入信号的信息，但是根据Brillinger定理[3]可以得到式（12）：
cum{xi(ω1),xj(ω2),xk(ω3),xl(ω4)}=0,
ω1+ω2+ω3+ω4≠2πK (12)
其中K为整数，这样，C40和C30就会为0，就很难估计输入信号的值。因此在这里尽量避开X(ω),利用类似于（6）、（7）、（8）式的方法，定义一组基于系统输出的互多谱的张量，为便于分析先从时域入手定义输出信号的三种不同类型的四阶互累计量：
在（16）和（17）中如果令ω1=ω2=ω3=ω则可得到与C31对应的频域的张量表示形式：
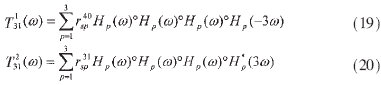
对应于实脉冲情况，可用（22）式的两个线性方程构成的方程组来实现对多项式G(ω)的估计。
同样的方法，可以通过（18）式得到其对应的张量如（23）式：
下面依次对式(24)中的参量进行估算：
(1) 估算∧(ω)：
对∧(ω)的估算可以借助功率谱" title="功率谱">功率谱，假定用PX(ω)来表示输出信号的功率谱，则：
摘 要： 基于高阶统计量（HOS）的分析方法，针对多输入多输出的MIMO系统中输入多于输出的情况进行了探讨，在对时域中其盲辨识原理进行分析的基础上，提出了一种基于频域分析的思路，以3×2 MIMO系统为例，基于互多谱累积量实现了MIMO系统的盲辨识，并对其实现过程进行了总结和仿真。
关键词： 高阶统计量 MIMO 盲辨识 互多谱
系统盲辨识的目标是通过n个系统输出来辨识系统的传输函数H(z)，通过H(z)估计恢复出系统的r个输入。MIMO系统的盲辨识有着很重要的应用，因为许多问题都可以归结为MIMO盲辨识问题。MIMO系统的辨识是对SIMO方法的扩展。本文提出一种基于频域分析的方法来辨识n×r的MIMO系统，其输入信号为独立同分布的量。通常情况下讨论的MIMO问题都是输出信号的个数n≥r[1]。这种情况下一般经过解卷积来恢复输入信号。在本文中考虑输入多于输出的情况，也就是说n
假定MIMO系统模型为：
x=Hs （1）
其中x=[x1(t)x2(t)]T 为二维输出矢量信号，s=[s1(t)s2(t)s3(t)]T为三维输入信号矢量，si(t)为零均值独立同分布非高斯白噪声，H为2×3维瞬态矩阵。为方便起见，定义以下累积量[2]：
∧为对角阵，ejΦ用来替代每一行的模糊相位。P为行交换矩阵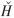，为混合矩阵的估计值，可以通过（9）式得到。这样即可通过（10）式得到H，从而由（1）式估计出输入信号。
2 基于频域实现的MIMO系统的盲辨识
为了更进一步方便对MIMO系统进行盲辨识，将（1）式进行傅立叶变换得到（11）式：
X(ω)=H(ω)S(ω) (11)
可以通过估计xi(ω1)、xj(ω2)……的互累计量谱得到输入信号的信息，但是根据Brillinger定理[3]可以得到式（12）：
cum{xi(ω1),xj(ω2),xk(ω3),xl(ω4)}=0,
ω1+ω2+ω3+ω4≠2πK (12)
其中K为整数，这样，C40和C30就会为0，就很难估计输入信号的值。因此在这里尽量避开X(ω),利用类似于（6）、（7）、（8）式的方法，定义一组基于系统输出的互多谱的张量，为便于分析先从时域入手定义输出信号的三种不同类型的四阶互累计量：
在（16）和（17）中如果令ω1=ω2=ω3=ω则可得到与C31对应的频域的张量表示形式：
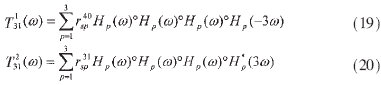
对应于实脉冲情况，可用（22）式的两个线性方程构成的方程组来实现对多项式G(ω)的估计。
同样的方法，可以通过（18）式得到其对应的张量如（23）式：
下面依次对式(24)中的参量进行估算：
(1) 估算∧(ω)：
对∧(ω)的估算可以借助功率谱，假定用PX(ω)来表示输出信号的功率谱，则：
其中P(p)即为所需要确定的交换阵，可以通过求解（27）式得到P(p)。
如果系统为最小相位系统，则到此即可对系统进行辨识，如果为非最小相位系统，则要继续下面的估算。
(3)估算ejΦ(ω)
相位的恢复可以借助（26）式进行推导，结合（24）和（26）式，得到：
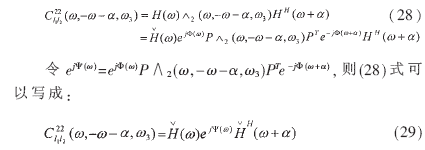
3 仿真
为了验证上述方案的可行性，本文按上述方法对一个非最小相位系统进行了仿真。其中n=2,r=3,DFT长度为128，H(z)表达式如(30)式：
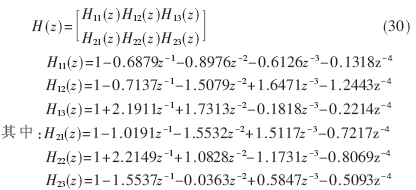
由图1可以看出，除0和?仔外，其他频率点的性能都比较好。
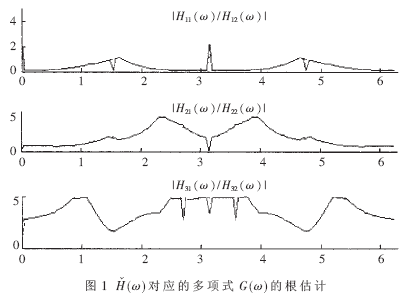
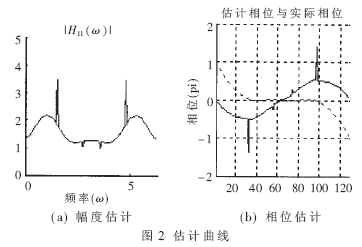
图2给出了幅度和相位估计的波形，图中虚线表示真实值，实线表示估计值，可以看出，只要通过改进0和?仔点的插入值就可改进估计的特性。
本文在对MIMO卷积系统盲辨识原理进行时域分析的基础上，提出了一种基于频域分析的思路，并且针对卷积MIMO系统中输入多于输出这一特殊情况，以3×2 MIMO系统为例，在频域中对其盲辨识的过程进行了探讨，最后总结出在频域中对MIMO系统进行盲辨识的一般步骤，该步骤方案的Matlab程序实现后经过仿真证明具有较好的信道性能。该步骤可以推而广之，扩展到所有输入信号数目大于输出信号数目的MIMO系统。
参考文献
1 Chen B, Petropulu A. Blind MIMO system identification Based on Cross- Polyspectra. In:34th Annual Conf. on Information Sciences and Systems,CISS′2000,Princeton University, 2000
2 Binning Chen, Athina P. Petropulu.Frequency domain MIMO system identification based on second and higher-order Statistics.IEEE Transactions on Signal Processing, 2001;49(8)1677～1688
3 Serviere C, Capdevielle V. An identification method of FIR digital filters in frequency domain.In:European Signal Processing Conference - EUSIPCO’1994, 2000
4 Binning Chen, Athina P. Petropulu. Blind identification of convolutive MIMO systems with 3 sources and 2 sensors.IEEE Transactions on Signal Processing, 2002
5 Jitendra K, Tugnait. Identification and deconvolution of multichannel linear Non-Gaussian processes using higher order statistics and inverse filter criteria. IEEE IEEE Transactions on Signal Processing, 1997;45(3)