内建自测试相移器设计算法的优化
2008-04-17
作者:吴 玺,刘 军,刘正琼
摘 要: 在原相移器设计算法的基础上,通过增加一个伪随机数生成函数来选择异或节点的相移器设计算法。实验结果表明,此算法不仅克服了原算法设计的相移器造成LFSR扇出" title="扇出">扇出过大的缺点,而且提高了伪随机测试" title="伪随机测试">伪随机测试故障的覆盖率。
关键词: 伪随机测试 混合模式测试 相移器 线性反馈移位寄存器 故障覆盖率
集成电路的发展已进入SoC时代,可将各种不同类型的IP芯核集成在一块芯片上,构成一个完整的系统,既能加快开发进度,又能提高系统整体性能。但集成电路的测试却面临越来越多的挑战,如不同类型的IP核测试方法不同,使得集成电路测试的复杂性大大提高。此外受芯片引脚数目的限制,IP芯核的I/O端口缺乏可观性和可测性。芯片的频率普遍高于自动测试设备(ATE)的频率,芯片的全速测试变得困难。内建自测试(BIST)是解决集成电路测试的有效方法之一。BIST将测试模式生成器、测试过程控制和测试响应评价功能模块嵌入在被测电路(CUT)上,摆脱了对ATE的依赖。这不仅是解决SoC测试问题的有效方法之一,也是SoC测试发展的方向[1]。
从测试模式生成器的角度,可将BIST分为伪随机测试[2]、确定测试[3]和混合模式测试[4]。伪随机测试是硬件开销最少的BIST测试方法,目前最流行的伪随机测试序列生成器是线性反馈移位寄存器(LFSR)。LFSR是由一系列D触发器经反馈线连接而成。LFSR有两类,两类LFSR互为对偶,如图1所示。图1所示LFSR都可用特征多项式1+h1x1+…+hn-1xn-1+xn表示。若hi=1表示第xi个触发器的输出经反馈线连接到异或门。
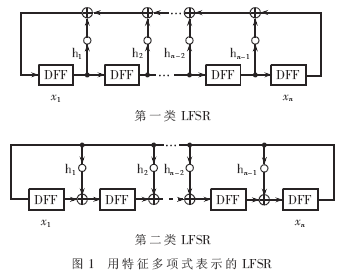
图1所示LFSR也可用矩阵M和D来表示。M为第一类LFSR的伴随矩阵,D为第二类LFSR的伴随矩阵。容易证明,MT=D-1[5]。

通过伴随矩阵,可以得到经过某个时钟周期后LFSR的状态。考虑第一类LFSR,设其值为V0=(x1,x2,…,xn),则经过P个时钟周期后,其值VP=V0×MP,即由LFSR状态V0向前模拟P个时钟周期可得到VP。由上式可得V0=VP×M-P,也可称为由LFSR状态VP向后模拟P个时钟周期得到V0。
在集成电路可测试性设计中,为节省测试时间,一般采用多扫描链的设计。若仅采用LFSR做为伪随机序列" title="伪随机序列">伪随机序列生成器,不同扫描链间的数据存在很大的相关性,如图2所示。
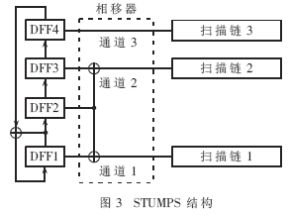
相邻的两个扫描链间的数据只差一个相位,大大降低了伪随机测试的故障覆盖率" title="故障覆盖率">故障覆盖率。为降低数据间的相关性,通常在LFSR和多扫描链间加上由异或门组成的移相器,这种结构称为STUMPS结构,如图3所示。

相移器打破了扫描链间数据的高度相关性,使相邻扫描链中的数据相差多个相位,提高了伪随机测试的故障覆盖率。因此,相移器的设计对伪随机测试的成功有着至关重要的作用。
文献[5]、文献[6]提出了相移器的设计算法,但此算法设计的相移器要求LFSR的某几位有很高的扇出,在实际的设计中,要增加反相器来增强这些节点的驱动能力,造成芯片的面积和时延增大。本文在分析和研究此算法的基础上,对其缺点进行了改进。通过增加一个伪随机数生成函数选择相移器的通道,使得LFSR节点扇出分布相对均匀。实验结果表明本算法是一种高效、实用的相移器设计算法。
1 相移器理论推导及算法
由图3可知相移器的通道输出都是LFSR某几位的异或,为描述通道的输出值,引入了相移器选择矢量。如图3通道2的选择矢量为S=(0110),表示LFSR第2个节点和第3个节点的异或值作为通道2的输出。设某一时刻LFSR的值为V=(v1,v2,v3,v4),则经过P个时钟脉冲" title="时钟脉冲">时钟脉冲后,通道2的输出值可表示为OUT2=V×MP×ST。ST表示S的转置。芯片实现时通常要求相移器有较小时延和面积,因此相移器的每个通道最多为 3 个节点的异或,即每一个通道选择矢量最多有 3 位为“1”。且为了打破不同扫描链间数据的相关性,任意两个通道之间的相位要大于等于某个确定的值。构建n个通道的相移器的问题等价于从LFSR的值域中选择n个值作为选择矢量,每一个选择矢量中的“1”的个数不大于3,且任意两个通道之间的相位要大于等于确定的值P。
设计相移器的关键问题是选择通道,使不同的通道输出之间的相位大于等于某一个确定的值P,这主要利用LFSR的性质。本文对此性质给出证明。
定理1:设有通道选择矢量Si和Sj,若将Si做为第二类(第一类)LFSR的初始值,经过P 个时钟脉冲后LFSR值变为Sj,则以其对偶的LFSR为伪随机序列发生器,以Si和Sj作为通道选择矢量构造的相移器的两个通道i和j输出序列相差P个相位。
下面以第一类LFSR作为伪随机序列发生器来证明此定理。
证明: 设第一类LFSR 的伴随矩阵为M,第二类LFSR的伴随矩阵为D。
比较式(1)和式(4),可知通道i和j的输出序列相差P个相位。
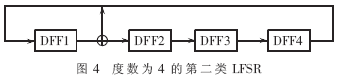
下面举例来说明定理1。如图4所示的第二类LFSR,若其初始值Si为(0110),经过15个脉冲后,其状态变为(1100),记为Sj。则可验证图3所示的通道2和通道3相差15个相位,其中Si和Sj为通道2和通道3的选择矢量。
文献[5]、文献[6]提出了两种相移器的综合算法,这里介绍执行速度快的算法(以第一类LFSR作为伪随机序列生成器构建相移器),记为算法A:
(1)生成“1”的个数不大于3的LFSR值的被选列表,令变量i=1,且将选择矢量列表清空;
(2)从被选列表中取第i个值,利用该值为第二类LFSR的初始值,然后前向仿真 P个时钟脉冲,后向仿真P个时钟脉冲;
(3)如仿真中出现的值与选择矢量列表中的值重复,则抛弃这次选择的值,否则将其加入选择矢量列表;
(4)如果选择矢量个数达到要求即停止,否则i加1,从第2步开始运行。
通过第2步与第3步就能保证选择出来的通道至少相差P个相位。通过一个4阶LFSR的实例来说明其综合过程。第1步生成的被选列表为:
{(1),(2),(3),(4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),(1,2,3),(1,2,4),(1,3,4),(2,3,4)}
如列表中(1,2,3)代表的是选择矢量(1110)。被选列表中第1个值(1)是符合条件的,将其添加到选择矢量列表中,然后再按照顺序判断(2)、(3)、(4)、(1,2)、(1,3)等组合是否满足条件。
从上述过程可看出此算法存在的缺点:产生的相移器对LFSR的某几位输出要求很高的扇出。这是因为每次该算法都是按照被选列表中值的顺序来选择符合条件的矢量,一旦选择矢量个数达到要求,算法就停止,后面符合条件的选择矢量没有得到利用。集成电路设计中,扇出过大,将会造成芯片面积增大,信号的建立时间过长等问题,最终可能导致设计的失败。本文采用的算法没有按照被选列表中值的顺序来选择符合条件的选择矢量,而是通过一个伪随机数生成函数来选择被选列表中的值,记为算法B,其算法如下:
(1)生成“1”的个数不大于3的LFSR值的被选列表,记列表中值的个数为k。令变量i=1,且将选择矢量列表清空;
(2)从被选列表中取第i个值,利用该值为第二类LFSR的初始值,然后前向仿真P个时钟脉冲,后向仿真P个时钟脉冲;
(3)如仿真中出现的值与选择矢量列表中的值重复,则抛弃这次选择的值,否则将其加入选择矢量列表;
(4)如果选择矢量个数达到要求即停止,否则i=rand()%k+1,从第2步开始运行。
其中rand()为产生伪随机的非负整数的函数。其函数实现如下:
int rand()
{next=next*1103515245+12345;
return((unsigned int)(next/65536)%32768);
}
next为无符号长整型静态变量,初始值为1。rand()函数输出一系列在0~32 767之间均匀分布的伪随机数值,产生的序列是可重现的,即程序每次运行都产生同样的一系列随机数。“%”为取余运算。在实际的设计中,为减小芯片面积,LFSR度数为48时,就可满足百万门规模的设计需要。此时被选列表中元素的个数为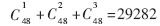 ,因此rand()函数返回值可取得被选列表中的所有值。从后面实验结果可看出,本算法构建的相移器不仅克服了LFSR某几位扇出过大的问题,而且通过此相移器生成的伪随机序列在电路的故障覆盖率方面也有所提高。
,因此rand()函数返回值可取得被选列表中的所有值。从后面实验结果可看出,本算法构建的相移器不仅克服了LFSR某几位扇出过大的问题,而且通过此相移器生成的伪随机序列在电路的故障覆盖率方面也有所提高。
2 实验结果及分析
表1为两种算法构建相移器时,对LFSR扇出的比较。选取第一类LFSR为基础构建相移器,度数为24,特征多项式为x24+x4+x3+x+1,相移器的通道数为100,两通道间的相位差p为1024。
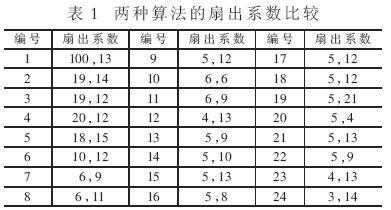
第1、3、5列为LFSR触发器的编号,其余列为两种算法扇出系数的比较。逗号前为算法A生成的相移器所需LFSR各位触发器的扇出系数,逗号后为本算法的扇出系数。从表1可看出,本算法LFSR各触发器扇出要求相比算法A要均匀。如算法A对第1个触发器的输出是100,而本算法为13。
混合模式的BIST首先对电路进行伪随机测试,然后对伪随机测试未测试到的故障采用自动测试模式生成算法(ATPG),对确定的测试向量进行测试。这里对国际上标准的ISCAS-89[8]部分电路做了实验,这些电路在10 000个伪随机模式之后仍有不可测试的故障。表2是LFSR通过两种算法设计的相移器生成10 000个伪随机模式对电路故障覆盖率的比较。选取LFSR度数为24,电路扫描链数量为48,LFSR初始值为(1010…10)。第1列为电路名,第2列为算法A设计的相移器生成的伪随机序列达到的故障覆盖率,第3列为本算法的故障覆盖率。
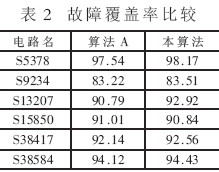
从表2可看出,除S15850外,本算法设计的相移器生成的伪随机序列故障覆盖率都高于算法A生成的相移器。这是因为LFSR的扇出分布比较均匀,各条扫描链间的相关性进一步减小,从而提高伪随机序列的测试故障覆盖率。而在算法A中,LFSR第1号触发器的扇出系数较大,受此触发器影响的扫描链较多,这些扫描链间的关系也相对要大一些。
本文提出了通过一个伪随机数生成函数来选择异或节点的相移器设计算法。实验结果表明,与原算法相比,本算法不仅克服了原算法扇出过大的缺点,而且生成的伪随机序列对集成电路测试的故障覆盖率也有所提高,在伪随机测试和混合模式测试中有一定的实用价值。
参考文献
[1] BUSHNELL M L,AGRAWAL D V.Essentials of electronic testing for digital,memory and mixed-signal VLSI circuits.USA:Kluwer Academic Publishers,2000.
[2] WUNDERLICH H J,HELLEBRAND S.The pseudo-exhaus-tive test of sequential circuits.Proc Of International Test Conference,1989:19-27.
[3] 梁华国,聚贝勒.海伦布昂特,汉斯-耶西姆.冯特利西.一种基于折叠计数器重新播种的确定自测试方案.计算机研究与发展,2001,38(8).
[4] 梁华国,将翠云.使用双重种子压缩的混合模式自测试.计算机研究与发展,2004,41(1).
[5] JANUSZ R,NAGESH T,JERZY T.Automated synthesis of large phase shifters for built-in seft-test.Proc of International Test Conference,1998:1047-1056.
[6] JANUSZ R,JERZY T.Design of phase shifters for BIST applications.Proc VLSI Test Symp,1998,218-224.