在数据采集系统中,模/数转换器是其中至关重要的环节。模/数转换器的精度以及系统的成本直接影响到系统的实用性,因此,如何提高模/数转换器的精度和降低系统的成本,是衡量系统是否具有实际应用价值的标准。
现在很多微控制器内部集成了A/D芯片,但常常达不到应用的要求,于是不得不浪费内部的A/D资源,花费资金去外扩一枚精度更高的A/D芯片。本设计实现了一种提高了已有的ADC分辨率的方法,适用于已有ADC分辨率达不到要求和精度要求不是特别严格的情况。
1 梯度均值A/D方案
定义1 设x为实数,[x]表示不大于x的最大整数,则称f(x)=[x]为x的取整函数。
定义2 设x为实数,
显然,令V通过量化单位为q的A/D系统,恰好等价于对x=V/q的量化运算(记为D=
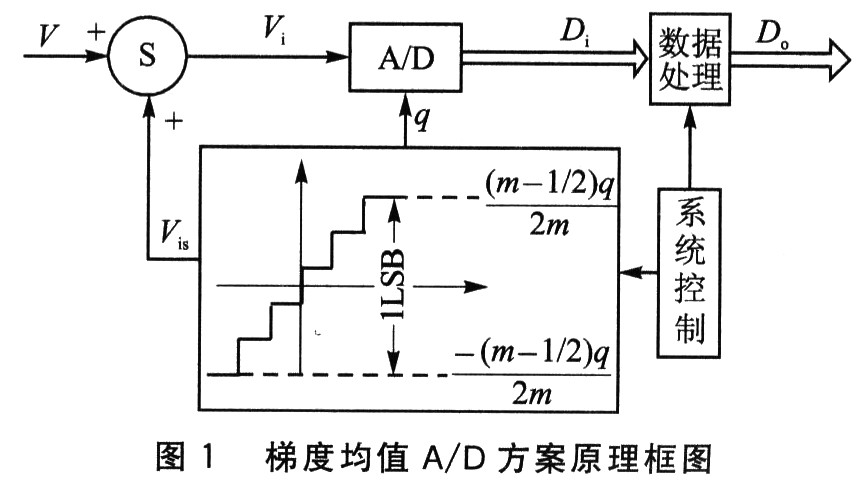
不妨称其中的A/D转换部分为基本量化系统,阶梯形输入信号为Vis,其幅度值
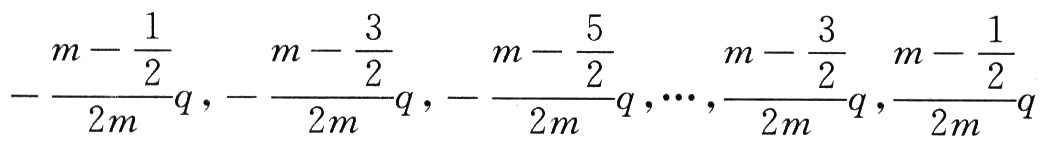
以等梯度递增,总幅度为1个量化单位q,其中m为正整数。该系统的输入信号V和阶梯波信号Vis依次叠加后送入基本量化系统,其量化输出信号Di输出到数据处理单元进行存储、处理。以基本量化系统的2m次Di的稳定量化输出的均值为系统输出,那么,有梯度均值A/D方案基本定理:设基本量化系统的量化单位为q,传递函数为
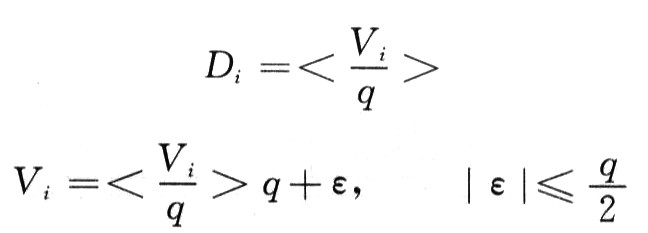
则图1所示A/D系统的等效量化单位为q/2m,传递函数为
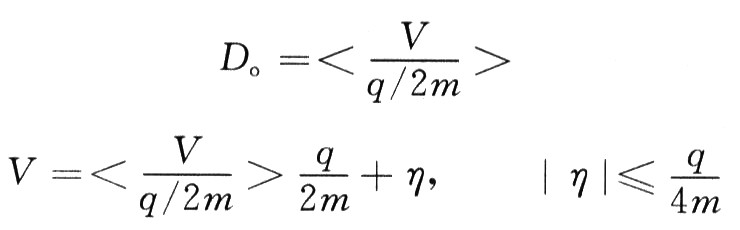
即系统容量扩大为基本量化系统容量的2m倍。
梯度均值法与统计均值法的性能比较:
①统计均值法每次采样必须读出被噪声干扰的第O.1LSB位,然而它是不稳定的;而梯度均值法每次采样只需读出1LSB位,该位是稳定的。因此,单次采样所用的时间,后者比前者要短。
②利用统计均值法,欲得到稳定的0.1LSB位输出,则噪声水平要降为1/lO(根据σ(.x)∝1/n),需采样100次;而梯度均值法只需采样10次,就可达到同样的效果。
③采用统计均值法,响应长,效率低。对于实时性要求高、需要快速响应的场合,采用梯度均值法效果更好。
2 系统设计
使用周立功公司的EasyARM2131开发板,并设计简单的外围电路。EasyARM2131开发板采用NXP公司基于ARM7TDMl一S核、单电源供电、LQFP64封装的LPC2138芯片,具有JTAG仿真调试、ISP编程等功能,提供RS232接口电路、I2C存储器电路、键盘、LED、蜂鸣器等常用功能部件,极大地方便了用户进行32位ARM嵌入式系统的开发实验。LPC2138内A/D的分辨率为10位,可以将其扩展为12位,甚至更高。
系统的原理示意图如图2所示,外围电路的核心是阶梯波发生器和同相加法器。

2.1 阶梯波发生器
LPC2138内部的D/A转换器是单极性的,只能生成单极性阶梯波,而梯度均值法要求使用双极性阶梯波。为此采用了差动运放电路,不仅将单极性阶梯波转换为双极性,而且进行降压,使阶梯波总电压幅度为A/D转换器的一个量化单位。具体电路如图3右半部分所示。
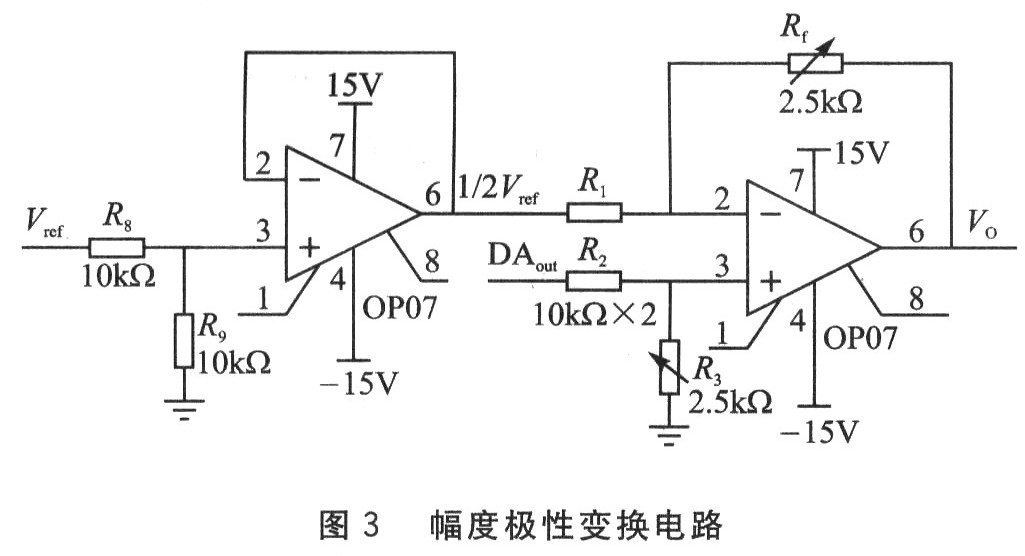
根据运算放大器“虚短”、“虚断”原则和叠加原理,求得
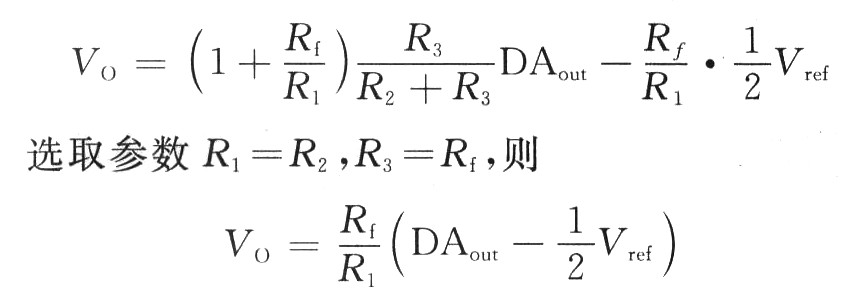
其中Rf为电位器,可以调节阻值并改变软件设置,提高A/D系统的精度。按照设计要求,阻值分别选择R1=R2=10 kΩ,R3=Rf=2.5kΩ,使Rf/R1=1/4。
幅度极性变换电路要用到(1/2)Vref,所以要由基准电压源分压得到。为了防止电压被拉低,增加一个电压跟随电路,如图3左半部分所示。其中,参数选择R8=R9=10 kΩ,运放使用OP07。
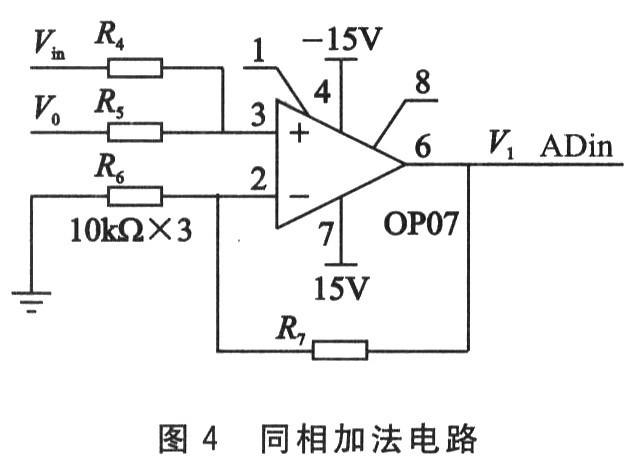
2.2 同相加法电路
同相加法电路如图4所示。参数选择R4=R5=1ckΩ,R6=R7=10 kΩ,所以V1=Vin+V0,其中Vin为输入电压,V0为阶梯波电压,V1输入到ARM内部处理。
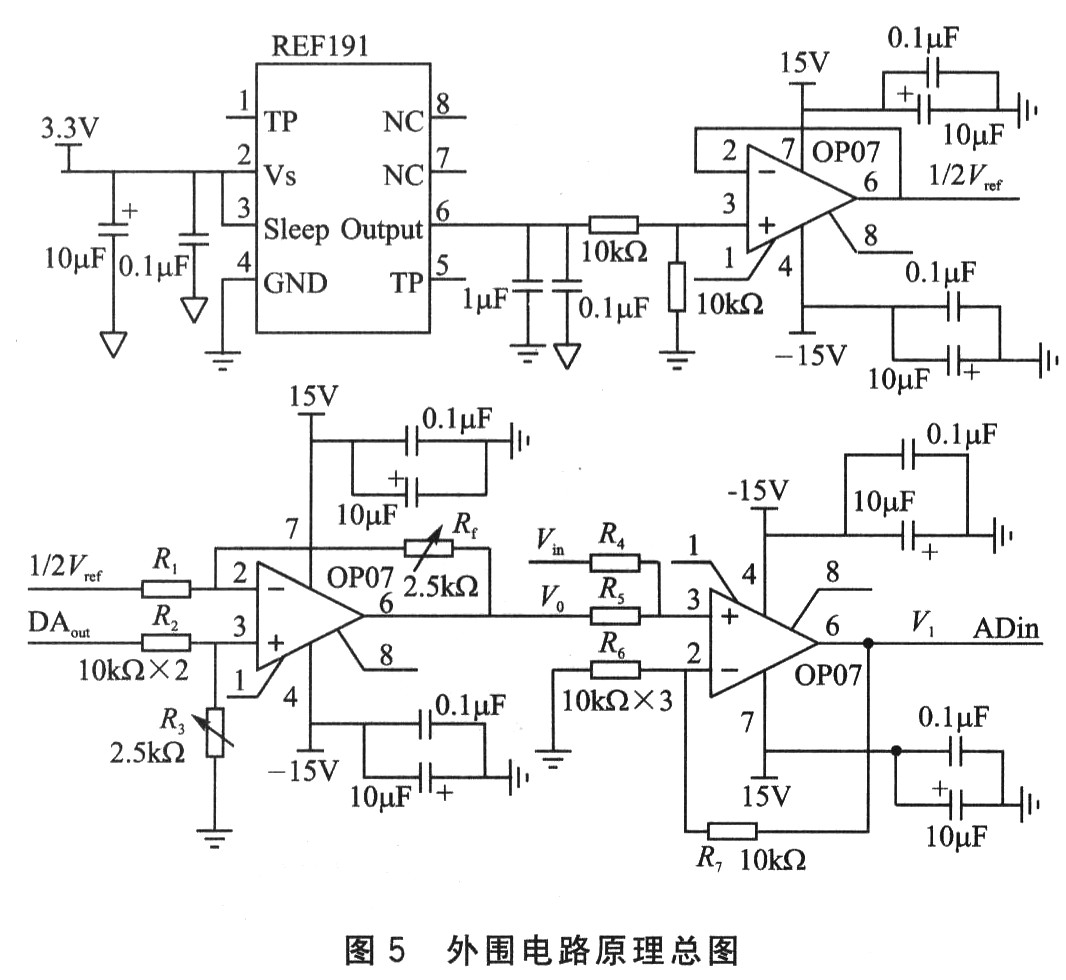
外围电路原理总图如图5所示。
3 系统软件设计
软件部分采用C语言编写,使用ADSl.2开发环境,并移植了μC/OS—II操作系统。细节见参考文献。
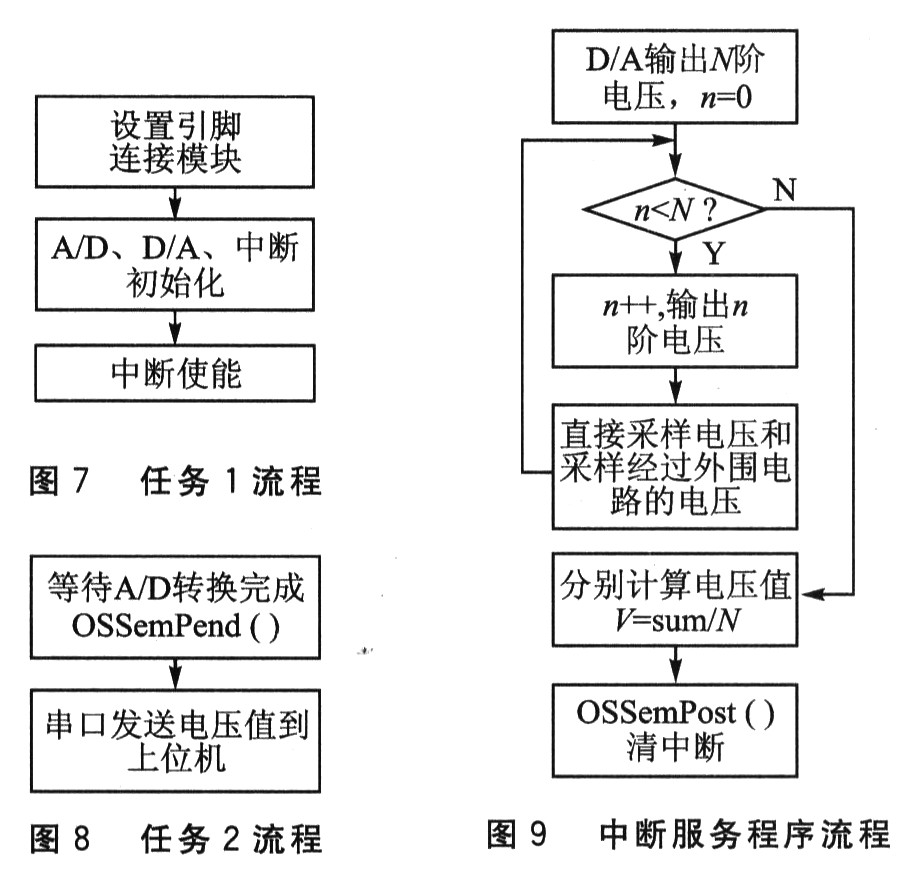
程序主要由以下几部分组成:主程序,负责初始化操作系统和创建任务;任务1,负责初始化目标板;任务2,负责目标板与上位机的串口通信;中断服务程序,负责采样和计算电压。各部分流程如图6~图9所示。

4 结 论
经过测试,该A/D系统测得电压比直接测量的电压更准确;A/D系统分辨率越高,测量的电压越准确。由于器件和工艺等原因,本系统有一定的误差,但基本达到设计要求,证明采用梯度均值法的A/D系统是完全可以实现的。而且如果采用更好的工艺和精密的元器件,还能提高本A/D系统的准确度。

