扩频控制技术用于减少电力电子变换器的电磁干扰的研究
2008-04-22
作者:黄 劲, 熊 蕊, 邹云屏
摘 要: 论述了一种对载波进行扩频" title="扩频">扩频控制以减少电力电子装置中变换器" title="变换器">变换器电磁干扰" title="电磁干扰">电磁干扰的方法。论证了扩频控制技术" title="控制技术">控制技术可以有效地降低载波及其谐波的峰值,讨论了不同的周期信号对正弦载波和PWM载波的扩频效果,同时指出了周期信号扩频可以有效地控制扩频后的带宽,便于滤波器的设计。最后探讨了扩频技术对特定频率点的干扰进行抑制的情况。
关键词: 扩频控制 电磁干扰 变换器 周期信号 PWM载波
在现代电力电子装置的实际应用中,为了便于谐波控制和滤波器的设计,广泛采用恒频变宽的PWM方式[1]。而电力电子装置中变换器所产生的电磁干扰(EMI)主要来源于开关器件的切换,高频的PWM控制信号使得开关切换频繁,加重了电磁干扰的产生,这种干扰主要表现在开关频率及其谐波频率的峰值上。
为了解决这个问题,首先考虑的方法应该是减少开关次数。虽然变频恒宽的脉冲频率调制方式(PFM)比恒频变宽的脉冲宽度调制方式PWM有更高的开关效率,但它的滤波器设计复杂。最近有人提出一种脉冲跨周期的调制方式(PSM)[2],它采用恒频恒宽跳脉冲的控制方法,非常适用于高频系统和轻载系统,因为脉冲的边际效应对EMI峰值的抑制有所帮助。
另一种方法就是主动降低开关频率及其谐波频率的峰值,从机理上降低EMI水平,所采用的方法就是对PWM的载波进行频率调制。根据帕斯瓦尔(Parseval)定理,只要信号保证时域能量分布不变,则频域的能量是守恒的[3],这就意味着如果扩展开关频率及其谐波频率的频带宽度,则各频带的峰值肯定会降低,从而减少EMI发射水平。对PWM的载波进行频率调制的方法有很多,国内文献见得较多的有随机调制技术[4-5]和混钝调制技术[6-9], 但由于它们的频带扩展得过宽(理论上趋于无穷),使得开关频率处的能量扩展到低频段,而低频段的EMI恶化,又不容易通过滤波器滤除,同时,变换器缓冲电路的设计也变得相当困难。最近,国外出现了用各种不同的周期信号对PWM载波频率进行调制的研究[10-12],如果选取频带有限的周期信号调频,就能避免能量过多地扩展到低频段,并且使滤波器和缓冲器的设计变得容易一些。
1 周期信号对正弦载波信号扩频
最典型的载波信号是正弦信号或余弦信号(统称为正弦信号)。假设未调制的载波信号为:
如果调制信号f(t)选用正负面积相等的周期信号,并适当选取坐标原点,使其偶对称(当然奇对称也是相似的推导),则它的傅里叶展开式为:


通过正弦信号扩频前后的频谱如图2所示。图中,取扩频前的载波频率fc点的峰值为0dB参考,可以看出,扩频后的频带展宽了,峰值也衰减了。扩频后的带宽通常用Carson准则进行估算[13]:
理论上扩频后带宽越宽,也就是mf和fm越大,峰值的衰减就越大。这里讨论在相同的mf和fm下,不同周期性调制信号的扩频效果。参考文献[10-12]中都只论述了调制信号是周期性的正弦波、三角波和指数函数,因此需要对其他典型信号进行对比研究。
这里选取周期性的正弦波、三角波、方波、梯形波、指数函数、抽样函数(即Sa(t)= 函数)和高斯函数(即Gauss(t)=
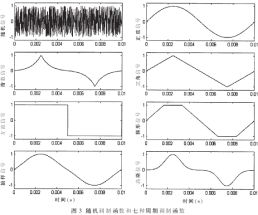
函数)和高斯函数(即Gauss(t)= )作为调制函数,为了对比,还给出了概率均匀分布的随机调制函数,如图3所示。除了随机调制函数外,其他七种函数的周期为fm=100Hz,用这八种信号对频率fc=10kHz的正弦载波进行扩频,调制指数mf=10。
)作为调制函数,为了对比,还给出了概率均匀分布的随机调制函数,如图3所示。除了随机调制函数外,其他七种函数的周期为fm=100Hz,用这八种信号对频率fc=10kHz的正弦载波进行扩频,调制指数mf=10。
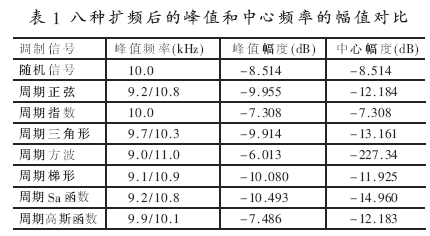
上述八种扩频后的频谱如图4所示。表1中给出了八种扩频后的峰值和中心频率的幅值对比。从中可以看出,周期正弦、Sa函数和高斯函数调制扩频后的带宽较小,随机调制和方波调制扩频后带宽较大,对低频影响较大。峰值衰减效果最好的是周期Sa函数调制扩频,周期梯形、正弦和三角形函数调制扩频后峰值衰减效果也比较好,周期方波函数调制扩频效果最差。实际上,方波函数调制扩频就是两点扰频,从实现的角度上来说是最容易的,从表1中也可以看出,它在载波的中心频率点上的衰减幅度最大。
2 周期信号对PWM载波进行扩频
PWM的载波是三角波,可以用类似正弦信号的定义方式进行定义:
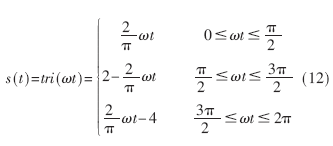
与正弦载波的调频相类似,三角载波调频后的信号为:
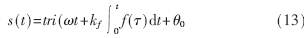
参考文献[4-12]所讨论的都是DC-DC变换器的PWM波,这里研究逆变器的PWM波的扩频。与前述正弦载波扩频相类似(所用参数也与前面相同),也用八种信号对PWM的三角载波进行调制,然后用调制了的三角载波调制工频" title="工频">工频信号(50Hz),产生PWM波。扩频前后的PWM波的频谱如图5所示,扩频前后载波频率附近的频谱如图6所示,在这里仍然以未扩频的PWM波的载波频率fc=10kHz的峰值为0dB参考。
从图5中可以看出,扩频的带宽随着谐波次数的升高而增大,和理论上一致。扩频后谐波处的带宽为:

式中,h为谐波次数。当谐波次数增大到一定程度时,相邻的谐波的谱线会因为扩频而相互混叠,因此高频时周期信号的扩频和随机调制的效果类似。表2给出了扩频前后工频、载频及其谐波频率附近的峰值对比。从中可以看出,除了随机信号、周期方波和周期高斯函数由于扩频后一些频率分量扩展到低频段,使得除在小于工频的频段其峰值水平与未调制的PWM频谱差异较大外,其它几种信号扩频前后变化不大。在工频频点处,这八种扩频后的幅值与原PWM的该频点的幅值相比,衰减程度很小,衰减最大的也没有超过6‰。这说明扩频控制技术不但适用于DC-DC变换器,也同样可以用在逆变器的控制中。在工频的绝大多数谐波附近,扩频后的峰值都有所降低,特别是对原PWM峰值水平较高处(如5倍工频),改善更为明显。在PWM的载波频率附近的扩频效果和对正弦载波的扩频相类似,只是由于调制指数选取得不太高(mf=10),随机调制的效果不明显,而在同样的调制指数下周期信号的效果较好,在PWM载波的谐波频率附近,扩频也同样获得了较好的效果。
综合考虑前面的分析和数据认为,从峰值衰减程度来看,周期正弦、三角波、梯形波和Sa函数的效果较好,而从硬件电路的实现上来看,周期正弦、三角波、方波和梯形波的产生较容易。
3 扩频控制对特定频点EMI抑制
前面讨论的是用扩频对PWM频谱的峰值进行衰减,是从源头上降低变换器的EMI发射。另一方面,变换器还会受到外界的电磁干扰。
假设逆变器在某个频点上受到了较强的干扰,同时,这个频点又在载波频率或者其谐波附近,那么可以用扩频方式进行抑制。
从图1可以看出,当mf=2.40,5.52,8.65,…时,J0(mf)=0,由式(10)可以知道,这意味着载波频率点的分量振幅等于零;而当mf为某些其他特定值时,又可使某些边频分量振幅等于零。根据这个原理,当载波附近的某个频点有较强干扰时,就可以通过选择适当的值进行扩频,让该点的干扰幅度降到最低。在载波谐波附近也可以如此。
前面的讨论都是基于扩频的初相位的情况,如果要更好地抑制干扰,必须考虑初相位θ0=0。只有这样,才能通过扩频,产生一个在干扰频点处与干扰信号幅度相当、相位相反的分量,去抵消干扰,达到抑制干扰的目的。
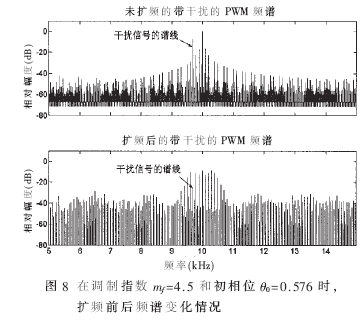
下面是在f=9.7kHz时人为地设置了一个加性单频干扰,用周期的Sa函数对PWM载波进行扩频,分析了调制指数mf=0~50、初相位θ0=0~2π时,抑制上述干扰的情况,如图7所示。图8给出了在最佳的mf和θ0时,扩频前后频谱的对比。由图可以看出,未扩频的干扰谱线幅度为-7.2dB,扩频后的干扰谱线幅度为-25.01dB,可见干扰有了明显抑制。

扩频技术原来是通信领域抗干扰的技术,是将基带信号(即信息)扩展到一个很宽的频带上,再用载波调制,从而降低对信道的信噪比的要求[14]。本文中提到的扩频控制在理论基础上虽然和通信中的扩频是相同的,但方法和目的不同。本文中的扩频控制是将载波信号扩展到一个很宽的频带上,再去调制基带信号(即工频信号),以达到降低PWM载波及其谐波频谱峰值的目的。
从前面的分析可以看出,周期性信号对PWM载波的扩频,可以有效地降低载波及其谐波峰值,从源头上降低EMI的产生水平,这不仅仅适用于DC-DC变换器,也同样适用于需要工频输出的逆变器。同时,周期信号扩频可以有效控制扩频后的带宽,便于滤波器的设计。另外,利用扩频控制技术,还可以抑制特定频率点的干扰。
总之,扩频控制技术在电力电子装置中变换器电磁干扰的综合抑制方面有广阔的应用前景。
参考文献
[1] 陈坚.电力电子学——电力电子变换和控制技术.北京:高等教育出版社,2002.
[2] 罗萍,李肇基,熊富贵,等.PSM开关变换器的平均模型与特性分析. 电工技术学报,2005,20(3):19-23.
[3] OPPENHEIM A V, WILLSKY A S. Signal & system(second edition). Prentice Hall International, Inc, 1997.
[4] 王斌. 抑制传导EMI策略——随机调制技术研究.三峡大学学报:自然科学版,2003,25(3):226-228.
[5] 王斌,李兴源, K El Khamlichi Drissi. 双随机调制技术及其功率谱密度特性分析. 中国电机工程学报,2004,24(4):97-101.
[6] 高金峰, 黄明明, 赵坤.应用混沌控制降低Boost型变换器EMI水平研究. 电力电子技术,2004,38(3):82-85.
[7] 汪剑鸣,许镇琳. 利用混沌提高dc/dc变换器的EMC性能. 电子科技大学学报,2004,33(5):586-589.
[8] 吴振军, 鲁静, 赵坤,等. 降低Boost型变换器电磁干扰水平的峰值电流控制方法. 郑州轻工业学院学报:自然科学版,2004,19(1):34-37.
[9] 高金峰, 黄明明, 赵坤. 应用混沌控制降低Buck型变换器电磁干扰水平研究. 电工技术学报,2003,18(6): 23-27.
[10] BALCELLS J, SANTOLARIA A, ORLANDI A. EMI reduction in switched power converters using frequency modulation techniques. IEEE Transactions on Electromagnetic Compatibility, 2005,47(3):569-576.
[11] MATSUMI Y, FUJII K, SUGIURA A. An analytical method for Determining the optimal modulating waveform for dithered clock generation. IEEE Transactions on Electro-magnetic Compatibility, 2005, 47(3), 577-584.
[12] JOHNSON J, ZANE R. Custom spectral shaping for EMI reduction in high-frequency inverters and ballasts. IEEE Transaction on Power Electronics, 2005,20(6):1499-1505.
[13] 谢嘉奎, 宣月清. 电子线路:第三版. 北京: 高等教育出版社, 1988.
[14] 曾兴雯,刘乃安,孙献璞.扩展频谱通信及其多址技术.西安: 西安电子科技大学出版社, 2004.