改进的自适应Zoom-FFT算法研究
2008-05-07
作者:王卫江
摘 要: 在分析了经典的Zoom-FFT算法的基础上,提出了一种改进的自适应Zoom-FFT(AZ-FFT)频域" title="频域">频域细化算法,通过比例因子" title="比例因子">比例因子的自适应取值算法和频谱调制校正算法,使得AZ-FFT算法运算量减少,满足了工程应用的实时性要求,且通过仿真验证了该算法的实用性能。
关键词: 频域细化 Zoom-FFT 自适应复调制细化 实时
在现代测量、自动控制等领域中,对一个宽带信号中的部分窄带信号进行快速频域细化分析,可以先用FFT(Fast Fourier Transforms)来对信号频谱进行粗略的估计,获取需要细化分析的窄带频谱范围;再在该窄带范围内进行频域细化分析,以获得满足精度要求的频谱[1]。
经典方法包括CZT (Chirp Z Transform) 算法、线性调频Z变换[2~3]、SDFT (Shifted Discrete Fourier Transforms)算法[4]、Zoom FFT算法(包括Yip级联Zoom FFT、复调制Zoom FFT、相位补偿Zoom FFT[5])等。
本文基于传统Zoom FFT和降采样数字信号处理的思想,提出了一种改进的自适应Zoom FFT算法,设计了一种能根据细化窄带带宽自适应地选择抽取倍数的降采样率算法,并改进了传统的复调制算法,能够实时得到更精细的细化频谱。
1 复调制细化分析Zoom FFT的基本原理[6]
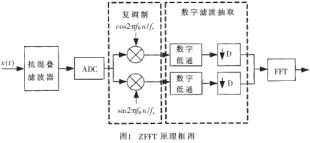
复调制细化是将时域信号与单位复指数相乘,将实信号变为复信号,根据傅立叶变换" title="傅立叶变换">傅立叶变换的频移定理,信号频谱产生平移,把感兴趣频段的中心频率移到相应频谱的原点处,再通过低通滤波及重采样后,做FFT变换后,得到更高的分辨率。其数据处理流程如图1所示。
模拟信号x(t)经抗混叠滤波、A/D转换后(采样频率" title="采样频率">采样频率为fs),得到数字序列x(n),其离散傅立叶变换(DFT)为:
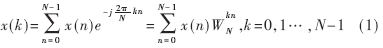
则DFT的频率分辨率" title="频率分辨率">频率分辨率为:△f=fs/N (2)
即Y(k)相当于X(k)左移L0点(L0=f0/△f),将f0移到零频。为了得到Y(k)零点附近的一部分细化频谱,可采用降采样的方法把重采样频率降到fD=fs/D,其中,D为降采样比例因子(D≥1)。为了保证重采样不产生频混,应先进行数字低通滤波,截止频率应为fD/2,此时滤波器的输出为:
Z(k)=Y(k)H(k) (5)
式中,H(k)为理想低通滤波器的频率响应,Z(k)为理想低通滤波器输出序列z(n)的傅立叶变换,其频率范围为0~fD/2。
以比例因子D对z(n)进行重采样,得到时间序列:
g(m)=z(Dm) m=0,1,…M-1 (6)
对g(m)做M点的DFT,其频率分辨率为:
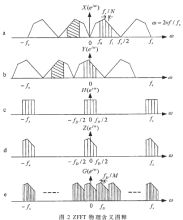
△fD=fD/M=fs/DM。当M=N时,△fD=fs/DN=△f/D,即细化后的频率分辨率比直接DFT的频率分辨率提高D倍。其物理含义如图2所示。
2 改进的自适应复调制细化分析(AZ-FFT)算法
从前面的分析可以看出传统的ZFFT存在如下问题:
(1)若以最大比例因子用上述方法进行计算,对信号复调制时,所需要调制的序列点数至少是DN点,即对DN点数据分别乘以单位复指数 。可见随着细化倍数的增加,计算量将显著增大,导致细化时间的剧增。
。可见随着细化倍数的增加,计算量将显著增大,导致细化时间的剧增。
(2)信号经过复调制、数字滤波和降采样后,将信号频谱从f0搬移到零频,使信号频谱在正频域和负频域不对称,从而细化后信号频谱与原始频谱不一致,导致频率分析误差较大。
针对上述两个问题,本文提出了相应的解决算法。
(1)比例因子D取值的自适应算法[7]
对序列x(n)做整数D倍抽取时,原序列的采样率降低了D倍,而抽取序列g(n)的频谱G(ejω)为原始序列的频谱X(ejω)经频移和D倍展宽后的D个频谱的叠加和:
流程图中的循环必定收敛于D≥1,而且循环一般能很早就收敛于较大的值。最后得到一系列的抽取倍数,选取适当的D值,D值越大,则细化的程度越大,但数据量也越大,需折衷处理。

(2)频谱调制校正算法
传统的ZFFT将感兴趣的一段频谱调制到以零频为中心、±B/2(B=f2-f1)的范围内,然后再进行降采样、FFT处理。但是由于对解析信号做FFT分析得到的频谱有效分布范围为(0,fs),如果按照图2中的调制方法,降采样后的FFT分析的谱图如图4(a)所示,其中负频率的谱线将折叠到fh~fD之间,发生错位时,需要做进一步的校正处理。如果在ZFFT做复调制时不按照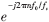 来调制,而是按照
来调制,而是按照 调制,即不是将f0搬移到零频,而是将f1搬移到零频,然后再做降采样、FFT处理,则分析的结果如图4(b)所示,谱线位置不会发生变化。
调制,即不是将f0搬移到零频,而是将f1搬移到零频,然后再做降采样、FFT处理,则分析的结果如图4(b)所示,谱线位置不会发生变化。

3 计算机仿真分析
设有一个加性高斯白噪信道中的低通模拟信号,带宽为200kHz,采样频率为400kHz,其中某个时段在150.2kHz、150.5kHz、151kHz、152.25kHz、153.375kHz处有单频信号存在。
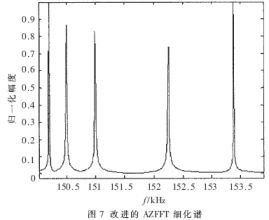
先对整个信号在200kHz带宽内进行512点FFT,粗略找出感兴趣的约4kHz的窄带(如图5所示),并求出不混叠的整数倍抽取倍数D,再对采样信号的150~154kHz范围内的频谱用自适应AZFFT算法进行细化。从图6和图7可以看出,采用改进的AZFFT算法细化后的信号频谱更加精确。
参考文献
1 Runtz K J, Hack D. A multistage DFT FFT CZT approach for accurate efficient analysis of sparsely distributed spectra [C]. Proceedings of 2002 IEEE Candian conference on elec-trical &computing engineering, 2002:127~132
2 Rabiner L R , Schafer R W, Rader C M. The chirp Z transform algorithm[J]. IEEE trans. on audio and electroa-coustics, 1969;17(2):86~92
3 应启珩,冯一云,窦维蓓. 离散时间信号分析和处理[M]. 北京:清华大学出版社,2001:1155~1591
4 李 勇,黄遵熹,俞卞章. 基于移位离散付立叶变换的线性频率估计方法[J]. 西北工业大学学报, 1995;13(3):414~4171
5 Hoyer E A , Stork R F.The Zoom FFT using complex mod-ulation[J]. IEEE Proceedings of ICASP, 1977
6 郭贵虎,胡新生.基于改进Zoom-FFT的信号检测算法研究[J].无线电工程,2003;(5):26~8
7 郭 瑜,汤宝平,纪跃波等. 基于解析信号和带通滤波的频率细化分析[J]. 重庆大学学报,2001;(7):17~21