引言
由于大型电子设备在进行电磁兼容" target="_blank">电磁兼容(EMC)性考核时,很难进入屏蔽室进行而只能在室外开阔场地进行,从而难以控制测试时的环境背景噪声电平,使测试结果出现很大误差。如何区分背景噪声信号,鉴别出受试设备发出的被测信号一直是EMC测试中的一个难题。在各种不同的背景信号中,同频干扰与被测信号无法通过频谱进行分离,本文的目的就是想用空间分离技术,通过适当的测试方法,对于任意方向的同频干扰信号进行有效的拟制,从而得到有效的测试结果。
消除同频干扰的基本方法
合成场分析
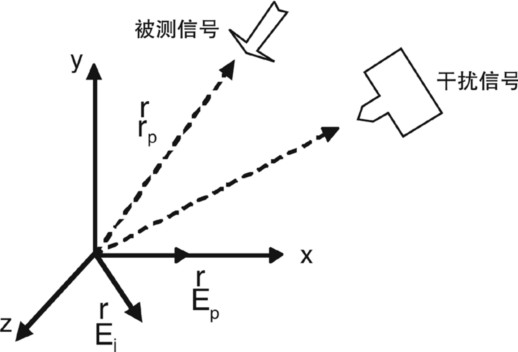
在图1所示的测试环境中,设待测信号与干扰信号均为线极化(在工程实际中,这样的假设是合理的),待测信号电场强度为:
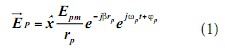
干扰信号电场强度
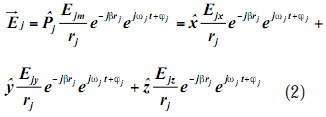
待测电场为向线极化,沿向传播,式(1)中Epm是被测信号源处的电场强度值;rp是被测信号到测试点的距离;wp是被测信号的初始相位;wp是被测信号角频率。
|
|
|
图1 电磁兼容性测试环境示意图 |
式中,Ejm是干扰信号源处的电场强度值,Ejx,Ejy,Ejz分别是,,方向的分量;rj是干扰信号到测试点的距离;是干扰信号的初始相位;是干扰信号角频率。
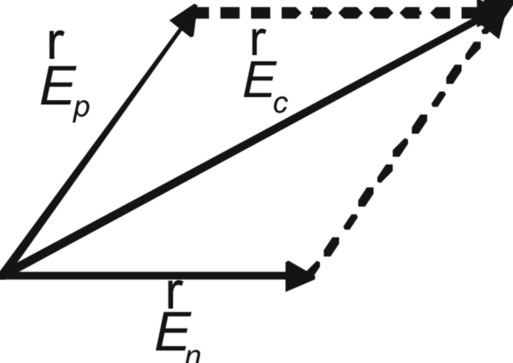
根据矢量叠加原理,则测试点处的合成电场强度
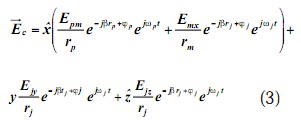
|
|
|
图2 矢量叠加示意图 |
测试天线使用线极化天线,将极化方向与被测信号一样调整到方向,则合成信号中的,向分量因为与测试天线极化方向正交被滤除,于是进入频谱仪的信号为:

因此频谱仪测得电场强度只包含与被测信号极化方向相同的干扰信号,而与被测信号极化方向正交的干扰信号对测量结果没有影响。于是在暗室模拟的干扰源的极化方向可与被测信号极化取为一致,设到达测试点的干扰信号为

由式(8)可以看出,当干扰信号与被测信号频率相同,而且距测试点的距离相当,电场强度值也相当时,在测试点得到的合成电场强度中无法鉴别出被测信号的电场强度。
因此在存在背景干扰的环境中进行大型电子设备的电磁兼容性测试,要解决的关键问题就是如何有效的减小背景干扰的强度,在测试点实现最大的信干比。由式(8)得,如果测试点处的信干比大于15dB以上时,即干扰信号的幅度远小于被测信号幅度时,叠加后的合成信号幅度可近似等于。
自适应天线消除噪声
阵列波束形成
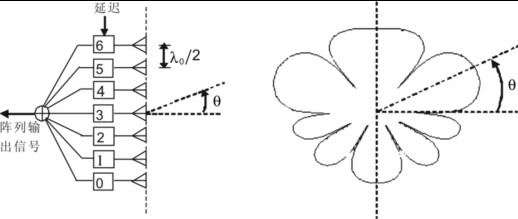
将一组以某种形式作空间配置的天线单元连接到一个或多个接收机(或发射机),就形成一个阵列。实际上,可以利用在不同(空间)方向上入射(或发射)的射频平面波与阵列天线中各个阵元处所具有的不同波程差延迟,并将各阵元射频信号分别作适当的延迟补偿后相加,以形成天线阵列的波束,其中被补偿最好的电磁波入射(或发射)方向将是阵列增益最高的方向,即阵列波束的方向。
图3为一个由七个天线单元组成的“线阵”。在这个线阵中,七个天线单元(均为无方向的全向天线单元)被排列成一条直线(也可以组成“面阵”,此时所有天线单元将布置在一个平面内)。图中各相邻天线单元之间的间隔均相同,且相距为,这里即为阵列工作的中心频率对应的波长。在阵列接收入射平面电磁波时,接收信号经各个天线单元的延迟补偿后相加输出。
在图3中,假定所采用的测试信号为,该测试信号的平面电磁波入射方向为,且各个全向阵元均具有单位增益,则在相邻天线单元间的波程差相位滞后(或超前)为:
|
|
|
( a)阵列结构 (b)天线阵E面方向图 |
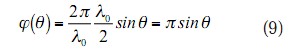
而用于各个天线单元的补偿时间延迟(单位为秒)所引起相位滞后为,于是可得阵列输出信号为
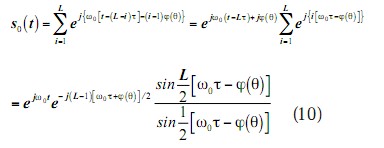
式中,L为天线单元数。
由式(10)可知,阵列的方向图函数的振幅为
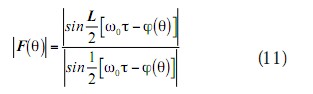
且当时,式(11)的值达到最大,即为方向图振幅的最大峰值点。而通过改变相邻单元间的时间延迟就可以改变方向图波束峰值的指向。
阵列波束方向图可以分布在的全部角度范围之内,由于在图3(a)所示的线阵结构中,阵面(由竖虚线表示)左、右两部分角度域是关于该阵面对称的,因而,如图3(a)所示的贞烈波束方向图也是关于阵面对称分布的。图中波束方向是在的角度范围里,此时用于延迟补偿的值应为正数(即相位滞后);而若要使波束方向被调整到的范围内时,就所需延迟补偿的值应为负数(即相位超前),当然这是物理不可实现的。然而,对于单频正弦波信号来说,可以用(其中为信号周期)代替这个负数的值,以达到波束方向调整的目的。
通常情况下,当阵列的各个相邻天线单元之间的间距大于时,会产生所谓“栅瓣”现象,即在的全部角度范围之内,方向图会出现两次或两次以上的重复。这样,在阵列接收和检测信号时,将会产生“空间模糊”,即阵列不能确定信号真实到达方向。
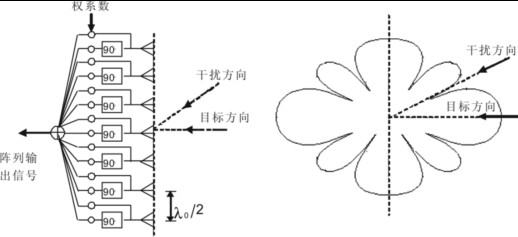
任意一种阵列的波束方向图除了主波束以外,都存在有副瓣。而当空间同时存在目标回波信号和不同方向入射的干扰信号时,要求阵列能在目标方向产生主波束,而同时能在干扰方向形成方向图零点。这样,若再用如图3(a)所示的阵列结构就不能满足实际需要了。图4(a)表示的线阵结构与图3(a)的区别在于,将各个天线单元的延迟补偿改换成正交两路加权的调整方法。通过调整这些权值可以同时得到所需要的主波束方向与方向图零深(增益极低)方向。对于单频正弦波信号而言,由于各个阵元的延迟补偿实际等效为乘一个复权系数,因而,每个阵元的同相信号与经90°移相后的正交信号分别由权系数实部和虚部相乘后就可完成对波束方向图的调整,且这种调整的自由度将增大。图4(b)是调整以后的波束方向图,它不仅将主波束对准目标方向,同时还在干扰到达方向形成了一个零深。
|
|
|
(a) 线阵结构 (b) 天线阵E面方向图 |