摘　要：基于跳频" title="跳频">跳频信号的特点,提出了一种隙同步的方法,并采用TMS320C54X系列DSP对隙同步方案进行了硬件仿真和分析。 

关键词：短波 跳频通信 位同步" title="位同步">位同步 TMS320C54X芯片 

    跳频通信是一种载频按照一定规律变化的多频率移频键控,具有抗干扰性强、保密性好、频带利用率高的特点,易于兼容,便于构成多种通信网。正是由于这些特点,跳频通信系统" title="通信系统">通信系统在现代军事和交通运输通信中得到了广泛的应用。国外近几年推出了大量跳频电台" title="跳频电台">跳频电台的产品,如美国HAKRIS公司的中速跳频电台RF-5010、美国Rockwell公司的SINGARS-U超快速跳频电台等。这些电台均采用微处理机控制,功能齐全,轻便灵活,操作简单。
　　利用跳频图案的良好正交性和随机性,可以在一个宽的频带内容纳多个跳频通信系统同时工作,将多个电台组成通信网络,完成专向通信或网络通信,达到频谱资源共享的目的,从而提高频谱的有效利用率,增加用户通信的灵活性[1]。短波信道是一种时变衰落信道,为保证各接收端" title="接收端">接收端均能在适当时刻进行取样判决,从而正确接收传输信息;短波跳频网对位同步有较高的要求。因此,位同步问题是短波跳频通信网中的一个重要问题。
　　位同步的实现方式很多,如常用的插入导频法和自同步法等。本文提出了一种新的同步方案——隙同步的概念,并基于TI 公司TMS320C54X系列DSP,采用TMS320汇编语言对该隙同步方案进行了硬件仿真和数值分析。
1 跳频网位同步原理
　　在跳频通信系统中,为了正确接收数据,接收端必须提供一个作为取样判决用的定时脉冲序列。该序列的重复频率与码元速率相同,相位与最佳判决时刻一致。因此,跳频通信系统位同步过程就是指收发两地跳频速率与起始相位的偏差在允许的范围内(通常小于1/2个码元)提取正确的定时脉冲序列的过程^[2]。基于跳频信号的特点,本文提出了一种隙同步的方法,可以较好解决短波跳频系统位同步问题。
1.1 隙同步原理
　　某段时间间隔内的跳频信号波形如图1所示。  

图1 跳频信号波形 

　　由图1可见,相邻两个跳频信号的载频频率是不同的,而且两个载频交界处的相位通常并不连续,存在突变。隙同步原理就是利用了跳频信号的这个特点来实现位同步的。
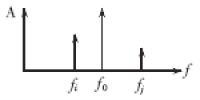
　　在图1中,从t0时刻开始提取一个码元长度的信号,通常在该段信号内包含着一个跃变点。若不存在跃变点,即码元准确同步,则跳频信号的幅度谱表现为如图2所示的单音信号形式。  

图2 同步时跳频信号幅度谱 

　　若在该段信号内存在跃变点,则信号的幅度谱将有所不同,在载频频率f0之外还有一些因跃变而产生的频率分量fi、fj等,这些分量的幅度较之f0要小得多,如图3所示。  

图3 不同步时跳频信号幅度谱 

　　由此可见,通过分析信号的幅度谱,可以判断跃变点的位置。具体而言,首先对信号均匀抽样得到长度为N的离散信号序列,对该离散序列进行快速傅立叶变换(FFT)得到其幅度谱,然后通过比较载频频率f0与相位跃变所产生频率分量的幅度,即可以判断信号是否同步。若因相位跃变而产生的频率分量的幅度之和为0,则表明信号已同步;否则,将信号延迟若干点,继续作N点FFT,直到信号同步。
　　以上讨论不存在噪声干扰的理想情况。然而,在实际应用中,噪声时刻存在,这使得信号即使同步了,除载频f0以外的各频率分量的能量也不会为0。但是在环境不十分恶劣的情况下,即当信号没有完全淹没在噪声中时,上述原理仍然适用。
1.2 隙同步实现方法^[3～4]
　　基于上述隙同步原理,本文设计了如下的同步点寻找方法:
　　(1) 以t0时刻为起始点取一段跳频信号,对该段跳频信号进行A/D转换得到离散信号序列。
　　(2) 从所得信号序列中顺序取出一个码片长度(N点)的信号,进行N点FFT运算得到该部分信号幅度谱。若该幅度谱中峰值对应的频率分量是约定频率之一,则将除该频率分量以外的所有频率分量的幅度求平方和,并记为a1,然后延迟W点(一般取W使N/W为整数),顺序取出N点信号,重复以上过程,直到完成N/W次(一个码片长度)的分析,所得的幅度和依次记为a2,a3,…,aN/W。若该幅度谱中峰值对应的频率分量不是约定的频率之一,则延迟W点取出后续的N点信号,重复上述操作。
　　(3) 从所得到的{a1,a2,…,aN/W}中取一个最小值ai,并将该点对应的时刻(即点序号)记为A1,初步认为该时刻即为同步点。A1可以根据下式计算,即
　　A1=startpoint+(i-1)×W(1)
　　(4) 重复(2)、(3)步骤,进一步得到A2、A3值。然后比较A1与A2、A2与A3的距离是否为一个码元的长度,若是,则表明所取同步点A1正确。
2 隙同步TMS320算法设计
2.1 隙同步程序
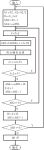
　　根据上述隙同步原理和同步点寻找方法,本文采用TI公司TMS320C54X系列DSP芯片^[5]进行硬件仿真,具体程序流程图如图4所示。  

图4 隙同步程序流程图 

　　为了便于数值仿真分析,本文将FFT运算所用到的余弦表值模拟为跳频信号的A/D输入数据,并规定一个码元周期内信号抽取点数为256点。具体输入数据设计如下:每个频率的数值表占用256个存储单元,存储顺序依次为选定频率的基频、倍频、4倍频、8倍频和16倍频值。
　　输入数据送入以addr1为首地址的数据存储区中,偶地址单元存储实部,奇地址单元存储虚部。指定C3为延迟指针,用于指定点搜索的起始位置。每次点搜索过程由程序控制将从地址(addr1+C3)开始的256个单元的数据送入FFT模块进行幅度谱分析,本文中C3每次移动8个数据单元。在判断峰值频率是否为约定频率之一时,通过约定频率的存储器位置进行判决,本文选取8个约定频率。
　　C1和C2为运算次数计数器。当C1＝32时,表示已经完成一个码元长度的同步点搜索,可以开始寻找32个和值中的最小值,否则继续计算。C2用于计算寻找到的同步点的个数。本文采用3个同步点辅助判断,因此,当C2＝3时即可进行同步判决。若同步成功,在程序结束时将地址大于3000的10个单元置1。
2.2 FFT算法设计
　　上述同步点寻找算法是一种基于信号频谱分析的幅度同步方法,对信号的幅度谱分析主要是利用快速傅立叶变换(FFT)算法完成的。因此,FFT算法的设计对上述隙同步方法是至关重要的。
　　按时间抽取FFT(DIT-FFT)算法是FFT算法的一种。它通过不断地把时间序列N点x(n)按照序号n奇偶性分解为偶序列和奇序列,并进行L＝log₂N级蝶形运算,从而减少乘法和加法的运算次数,尽可能地减小运算量^[6]。
　　DFT变换式为: 

根据旋转因子的周期性和对称性,可以将X(k)进一步表示为:

　　
　　式(3)中,X1(k)和X2(k)分别为偶序列和奇序列的N/2点DFT。由此可见,只要求出0到(N/2-1)区间内的所有X1(k)和X2(k)值,即可求出0到(N-1)内所有X(k)值,这就大大节省了运算。
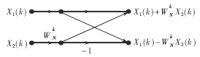
　　利用蝶形信号流图,(3)式可以表示为如图5所示的蝶形运算形式。  

图5 蝶形运算单元 

　　对于N点的FFT运算,共包含有L=log₂N级蝶形运算。通过不断对序列进行奇偶序列分解,即可以得到N点FFT运算的流图。根据DIT-FFT算法的特点可知FFT程序设计有如下三个关键的问题:
　　(1)输入序列应该是反序输入,即按照序号n的比特反转值输入;
　　(2)与各级蝶形单元相应的旋转因子值的确定;
　　(3)蝶形单元的控制,包括输入数据的读取、输出数据的存储及时序控制等。
　　FFT算法的流程图如图6所示。  

图6 FFT算法的流程图 

　　根据短波跳频信号的特点,本文提出了一种新的跳频通信网位同步方案——隙同步的方法,并基于TI公司TMS320C54X系列DSP,采用TMS320汇编语言对隙同步方案进行了硬件实现和分析。
　　仿真结果表明:隙同步原理能较好地解决跳频通信网中接收端的位同步问题,为后续单元实现正确译码奠定了基础。而且,由于TMS320C54X系列DSP具有运算速度快、精度高的特点,采用该方法可以获得较短的同步时间,有利于提高通信网的性能。
参考文献
1 胡中豫.现代短波通信[M].北京:国防工业出版社,2003:222～246
2 Li Weidong, Wang Jing, Yao Yan. Synchronization design of　frequency-hopping
  communication system[C]. ICCT’98.Beijing,China:1998(10):S13-01-1～S13-01-5
3 Marvink.Simon, Jimk.Omura, Robert A.Scholtz,etc.扩频通信技术教程(英文版)[M].
  北京:人民邮电出版社,2002;958～1022
4 甘良才,阚爱武.基于短波FH/DQPSK系统的FFT同步方案[J].电波科学学报,2001;16(3):390～393
5 戴明桢,周建江. TMS320C54x DSP结构、原理和应用[M].北京:北京航空航天大学出版社,2002
6 程佩青.数字信号处理教程[M].北京:清华大学出版社,1995:215～252