近年来，数字水印技术在抵抗压缩、滤波等方面得到了快速发展，出现了许多基于DCT和DWT的频域优秀算法。
　　数字水印系统模型如图1所示。水印信息W在密钥K的控制下嵌入到载体图像C中形成水印化图像Cw。水印化图像在发布过程中可能遭受到包括几何变换攻击在内的各种处理，等效于经过一个攻击信道。几何变换会使水印能量分散，位置改变。具体变化与几何变化中采用的插值" title="插值">插值操作方式有关，有时即使知道精确的几何变换条件，也不易实现水印的完全提取^[1][2]。因此，一般算法难以抵抗旋转、缩放和平移等几何处理所造成的去除同步攻击，抗旋转类几何攻击的水印技术开始成为第二代水印技术研究的重点。

　　为了解决几何变换类攻击问题，众多学者进行了大量研究并提出了一些算法^[3][4]，其中最具代表性的有：(1)基于Fourier-Mellin变换水印算法：在图像几何不变域中嵌入水印信号，对旋转和缩放处理具有不变性，但其缺陷是插值操作极易恶化图像质量，同时造成水印信号的损失。(2)基于模板匹配的水印算法：除水印信号外，在图像中还嵌入模板信号，通过几何处理前后模板信号之间的匹配估计图像几何处理参数进行恢复。不足之处在于模板信号具有的规则结构和显著取值，使攻击者能够成功地扰乱或去除图像中的模板信号；且需要采用穷举搜索的策略进行参数估计，增加算法的复杂度。(3)基于图像特征的水印算法:图像的显著特征对视觉系统有较好的不变性，利用图像的底层特征可对水印信号的检测进行同步。然而如何自动、可靠地提取这些特征(尤其是图像受到若干处理的情况下)始终是模式识别领域的一个难点。(4)校准信号几何同步方法：该方法可以实现常见几何变换的估计与同步,但几何逆变换操作是实现水印检测的必须步骤，这样二次处理中的插值运算使用越多，水印信息丢失越多。
　　鉴于上述原因，考虑无需对遭受几何攻击图像进行恢复校正，而是根据其经历的几何变换追踪水印信息的新位置，因而提出了水印扇区块的概念，即依据三元组^[5]思想在水印扇区块中嵌入和提取水印，通过霍夫变换估计图像的旋转角度。由于未对载体图像作二次处理，因此最大可能地保存了剩余其中的水印信息。
1 算法设计
1.1 图像小波变换" title="小波变换">小波变换细节子图中植入基准线
　　小波变换是近几年兴起的一种可以达到时域或频域局部化的信号时频分析方法，其多分辨率处理能力及频带的多尺度划分与人类的思维方式和生理功能相吻合；基函数灵活多样，是一种快速的线性运算；图像经过小波多分辨率分解后，能量几乎都集中在较低频的子图像上，在低频逼近子图上嵌入的水印稳健性强；人眼对高频分量的改变不敏感，所以在图像细节子图上添加一个隐蔽的基准线，被用来测试图像旋转角度β，不会引起图像失真。
1.2 霍夫变换估计旋转角度
　　水印提取时，对待测图像一级小波分解后的细节子图进行霍夫变换(坐标原点选择为图像的中心点，极角的范围为θ∈[0，2π]，角度间隔△θ=1°)，检测前先添加其中的基准线；选取具有最强方向的一条直线P(即添加的基准线)，根据式(1)计算其角度的改变，即图像的旋转角度(负值表示顺时针旋转，正值表示逆时针旋转)：
　　
　　图像实际应用中通常只进行小角度旋转，因此在使用上式计算旋转角度时隐含一个假设：即图像旋转的角度不超过45°，霍夫变换中极角取值间隔为1°，因而旋转角度估计的精度为1°。
1.3 扇区块水印嵌入
　　扇区块的角度变化如图2所示。为便于水印的定位和准确计算，提出了水印扇区块的概念：在图像一级小波变换的低频子图LL中，以其中心为圆点，低频子图被划分为许多扇道，选择同一扇形(10°)中标记为1、2、3的三个扇区块，并依据它们的线性关系嵌入水印。如果图像遭到旋转攻击，标号为1、2、3的扇区块就从原位置旋转到新位置。这样只要知道旋转角度就可以方便、准确地定位三个扇区块的新位置1′、2′、3′，然后进行水印的检测。

　　
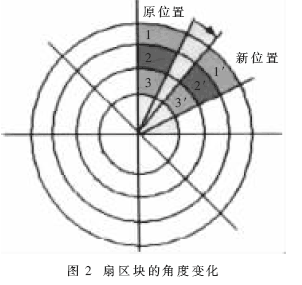
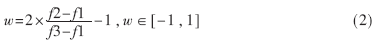
　　借鉴三元组思想：定义三个扇区块的块均值从小到大依次为f1、f2、f3，依据式(2)改变块均值间的线性关系来隐藏一位信息：如果要嵌入1，将中间值f2与最大值f3取相同；如果要嵌入-1，则与最小值f1取值相同。该块在未被改动的情况下，依据公式(2)计算所提取出的信息应为1或-1。
　　当图像发生旋转时，三个扇区块也发生同角度的旋转。图像旋转后，不同位置扇区块元素值会有所改变,但它们的改变方向是一致的，只要扇区块中的元素足够多，旋转后各块均值间就能够保持这种线性关系。考虑到如果f2改变太大，会引起图像失真，为了维持水印的不可见性，实验数据表明在保证水印不可见性基础上为了满足最大嵌入强度要求，f2的改变不应超过其本身的 50%。
　　图2所示圆形区域有4个象限，同一位信息存贮在4个象限的不同位置，这样水印信息被重复嵌入，当某处信息被破坏后，还可以通过其他处的“后备”来重构。以每一处提取的隐藏信息为权值，在重构时对各处的提取值进行加权平均值计算，这样得到的重构水印更加准确。
2 水印算法描述
2.1 水印生成
　　为保证水印保密性，采用了线性移位寄存器产生的m序列作为被嵌入的二值水印信号(-1，1)，记为W，水印长度为K，W={w(k)|0≤k≤K，w(k)∈(-1，1)}：m序列发生器的种子作为密钥保管。
2.2 水印嵌入
　　水印嵌入步骤如下：
　　(1)对图像I进行一级小波变换，记作Y=DWT(I)。
　　(2)在细节子图HH中添加基准线P。
　　(3)在逼近子图中划分扇区块，从第一象限第一扇区开始，计算三个扇区块的块均值，自小至大为f1、f2、f3。
　　①若嵌入-1，当f2-f1＜50%×f2时，则将块2中的每个值减(f2-f1)，使得块均值f2=f1；否则使f2=f2×(1-50%)；
　　②若嵌入1，当f3-f2＜50%×f2时，则将块2中的每个值加(f3-f2)，使得块均值f2=f3；否则使f2=f2×(1+50%)。
　　(4)对每一位水印信息W(k)在4个象限重复步骤3 进行嵌入。
　　(5)将所有水印信息嵌入后，进行逆DWT变换，还原回原图位置，构成了水印化加密图像I′。
2.3 水印提取
　　水印提取是嵌入的逆过程，具体步骤如下。
　　(1)对水印化图像I′进行一级小波变换，在细节子图HH中通过霍夫变换计算图像旋转角度β。
　　(2)根据旋转角度β，追踪三个扇区块的新位置，计算三个扇区块块均值f1′、f2′、f3′。
　　(3)根据式(2)计算每块中隐藏的信息。式(2)中，若f3′=f1′，则可令w=0。w的绝对值越接近1，说明提取信息的准确性越高；w越接近0，说明图像被改动越大。
　　(4)在4个象限重复进行步骤(2)~(3)，得到4个同样表示第k位水印的信息w，计算这4个信息的带符号算术平均值W(k)＜sup>s＜/sup>，k=0，1，……K-1，W(k)＜sup>s＜/sup>∈[-1，1]；若W(k)＜sup>s＜/sup>≥0，则第k位水印信息W(K)′=1；否则W(K)′=-1。这样就构成了检测到的水印W′，W′={w(k)|0≤k≤K，w(k)∈(-1，1)}。
　　(5)用作为密钥保管的种子，通过同一线性移位寄存器产生与水印嵌入时相同的m序列W，比较W与W′的相似程度，以确定图像中是否含有水印。
3 实验结果及分析
　　仿真实验采用的载体图像是512×512的256级灰度图像Lena，水印长度 54b。在VC＋＋6.0平台对上述算法进行了编程实现。公式(3)定义的峰值信噪比PSNR被用来衡量水印化图像与原始载体图像的质量差别，其中I(i，j)和(i，j)分别表示原图像和水印化图像中对应位置的像素。公式(4)定义的相关系数NC被用来衡量提取的二值水印图像与原始水印图像的相似程度，其中的w(i)和wx(i)分别表示第i位原始水印和第i位提取水印。
　　
　　图3为原始图像，图4为嵌入水印后未经攻击的图像，PSNR值达到35.57，算法基本保证了水印的不可见性，从中提取的水印与原始水印完全相同。图5为水印化图像旋转5°的情形，图6为检测到的基准线，旋转角度估计完全正确，提取水印与原始水印相似度为0.94。

　　文献^[6]是一种较理想的抗旋转攻击方法，表1对两种方案进行了实验比较。从中可以看出，本算法在遭到旋转攻击后能较准确地提取出水印，小角度旋转后的水印提取性能明显较高。
　　几种类型攻击后提取的水印相似度NC如表2所示。从表中看出，本方法作为一种小波域水印算法，在载体图像的逼近子图中嵌入水印，使得算法具有较好鲁棒性。引入三元组扇区块概念后，水印重复嵌入，水印被散布处理，因此对于涂抹和剪切等几何型攻击具有很好的抗攻击能力，提高了水印提取的准确度；而用于检测图像旋转角度的基准线则在细节子图中嵌入，其嵌入强度选取合适，既不容易被察觉，又具有稳定性，经过霍夫变换后能准确检测出图像旋转的角度。