近年来，随着雷达和干扰技术的不断发展，电磁领域的斗争越来越激烈。雷达在突破传统体制的同时，不断追求理论和技术上的进步，而这一切的努力都是为了雷达能在电磁斗争中取得优势，即在被干扰的情况下尽可能地发现和跟踪目标，即提高在干扰条件下的雷达最大作用距离和发现概率[1～2]。在实战中，雷达通常工作在复杂的电磁环境中，为了提高在干扰条件下的雷达作战效能，必须对噪声干扰进行有效的抑制。但是，现有评估雷达作战效能都是从雷达最大作用距离或发现概率出发，没有从干扰信号" title="干扰信号">干扰信号角度讨论。本文以信噪比为纽带，建立机载雷达接收端的噪声干扰模型，对干扰模型进行分析，建立一种Remez变换算法的线性相位FIR数字滤波方法，对噪声干扰信号进行处理，以抑制噪声干扰效能，为评判标准对综合评估机载雷达作战效能提供重要的参考依据，最后通过仿真比较说明该方法的合理性。
1 基本原理
　　针对干扰对抗实际环境、干扰效果度量的基本框架如图1所示，图中环境信号模型主要是建立目标、噪声环境以及干扰信号模型，用于模拟接收信号。信号处理机的实时滤波特性是其抗干扰的主要措施，包括脉冲压缩、滤波处理、目标检测技术等模块，其模块结构如图2所示。各种抗干扰措施输入前后的信干比增益是主要的度量指标。干扰效果度量则是建立干扰效果度量的准则，从而根据抗干扰措施前后的总的信干比增益，评价其抗干扰效果。

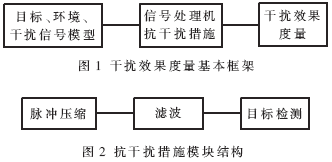
　　本文主要用线性相位FIR数字滤波方法对干扰信号进行处理，根据抗干扰措施前后信干比的变化，以及由此带来的对雷达最大作用距离和发现概率的影响，建立了抗干扰措施的数学模型，并利用信干比的测量结果合理完善该数学模型，从而为综合评估机载雷达作战效能提供重要参考。
2 数学模型
2.1信号模型
2.1.1雷达接收端接收信号模型
　　常用雷达信号为窄带信号，其发射信号可以表示为：
　　s(t-nT)=Re[u(t-nT)exp(jω₀(t-nT))]　　　　(1)
　　式中Re表示取实部；u(t)为调制信号的复数包络；ω₀为发射角频率，即工作频率，而T则为脉冲重复频率。
　　由目标反射的回波信号sr(t)则可以表示为:
　　s_r(t-nT)=ks(t-t_r)=Re[ku(t-t_r)exp(jω₀(t-nT))　　　　(2)
2.1.2 噪声干扰模型
　　噪声干扰的模拟主要考虑有源噪声。在理想条件下，雷达对目标的检测能力仅受到接收机热噪声的限制^[4]。然而，在电子战条件下，雷达受到噪声干扰时，必须用等效的噪声功率密度来分析干扰的效能。
　　如果干扰中心频率为f₀，接收机中心频率为f_s，则到达接收机的干扰功率P_rj为:
　　
　　式中，P_j、G_j分别为干扰机功率、指向雷达方向的干扰天线增益；γ_j为极化系数，B_j为干扰机工作带宽，B_r为雷达接收机带宽。雷达的噪声干扰方式的效果体现在干扰机工作带宽B_j占雷达工作带宽B_r的百分比。式(3)考虑B_j＞B_r的情况；若B_j≤B_r，认为B_r＞B_j=1。
2.2 典型抗干扰措施模型
2.2.1 噪声调频干扰模型
　　噪声调频干扰是目前应用最广泛的压制干扰形式，它具有较宽的干扰频带，但干扰功率密度低。其干扰电压的表达式如下所示：

2.2.2 滤波模型
　　(1)抑制干扰信号的数字滤波技术的特点
　　在一个实际的机载雷达中，如果使用一个数字滤波器组，则它对经过接收机、频率转换、视频采样和A/D变换后的信号进行频域检测，从而将目标信号识别出来，如图3所示。
　　(2)FIR滤波器的窗函数设计法
　　设h(n)(n=0,1,2，…，N-1)为滤波器的冲激响应，输入信号x(n)，则通过Z变换后得到的FIR滤波器的传递函数为：
　　
　　由式(6)可看出，FIR滤波器的一般结构如图4。

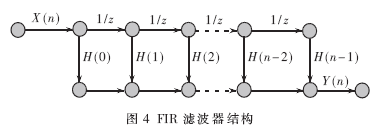
　　窗函数设计法是一种通过截短和计权使无限长非因果序列成为有限长脉冲序列的设计方法。该方法的基本思想就是选择一个适当的窗函数，在时域中用有限序列的窗函数w(n)与滤波器的单位脉冲响应进行乘积运算。根据技术要求确定待求滤波器的单位取样响应h_d(n)。如果给出待求滤波器的频响为H_d(e^jω)，那么单位取样响应用下式求出：
　　
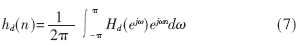
　　按照过渡带及阻带衰减情况，选择窗函数形式。原则是在保证阻带衰减满足要求的情况下，尽量选择主瓣窄的窗函数。
　　(3)Remez变换算法的FIR数字滤波器设计
　　通常，长度为N的线性相位FIR数字滤波器由于h(n)的长度N取奇数还是偶数，对它们的幅度特性H_g(ω)有影响，因此对线性相位FIR滤波器的4种不同情况进行了讨论，如表1^[2]所示。
　　经过推导可把H_g(ω)统一表示为：H_g(ω)=Q(ω)P(ω)，式中P(ω)为系数不同的余弦组合式，Q(ω)是不同的常数。E(ω)则可近似表示为：
　　
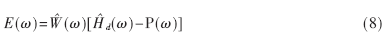
3 仿真分析
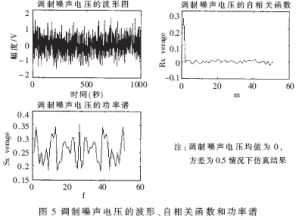
　　设定：干扰噪声为均值0，标准偏差为0.5的高斯白噪声，其调制噪声电压的波形、自相关函数和功率谱见图5。

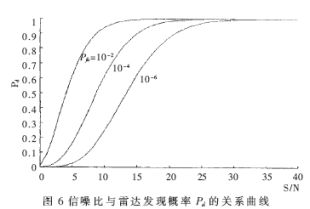
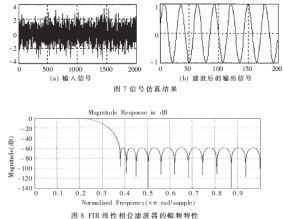
　　假如0.2kHz正弦调制信号，其中噪声功率是输入信号的4倍。这样从输入信号中看不出原始信号的波形来。信号的采样频率f_s=1kHz。图6为在虚警概率P_fa=10^-2、10^-4、10^-6时信噪比与雷达发现概率Pd的关系仿真曲线，图7(a)为混有噪声的输入信号，图7(b)为滤波后的信号，图8为FIR线性相位滤波器的幅频特性。

　　从以上结果可以看出：
　　(1) 从图6的仿真结果可以清楚地看到雷达接收端的信号噪声比与雷达发现概率之间的关系。由此得到如下结论：在相同的信号噪声比情况下，虚警概率越小则发现概率越小；为了获得相同的雷达发现概率，虚警概率小的雷达接收端必须具有较高的信号噪声比；对于同一虚警概率情况下，随着信号噪声比的增大，雷达的发现概率也在增大。
　　(2) 对比图7(a)和图7(b)可以看出，干扰信号在高频段有很强的能量分布，因此选择合适的分析频带可有效地抑制噪声干扰信号而保留有用信号。经过数字滤波后，信号的频率成分确实得到了很明显的改善，附加在有用信号中的高频噪声成分被FIR滤波器有效地滤除掉了，仅仅保留了有用信号的基本成分，使得信号本身的确得到了较为明显的改善。
　　(3) 由图8可知，该滤波器具有最大平坦通带和等纹波阻带幅度特性，通带边缘频率0.2π，通带加权W(ω)=1，阻带边缘频率0.3π，阻带加权W(ω)=10，这样通带波纹δ1=0.058 2，衰减为0.491 6dB，阻带衰减为44.7dB。通带平坦度L=6，在ω=0和ω=π角频率上传递函数为零。
　　综上所述，基于Remez算法设计的线性相位FIR滤波器性能优异，适用于信号的实时抗干扰处理，并能有效地提高雷达系统信噪比，为综合评估机载雷达作战效能提供重要的参考价值。这与实际抑制干扰信号的要求完全相符，说明该方法的合理性。