RFID主要由阅读器和应答器两大部分组成。阅读器（如图1）是数据捕获系统，内含一个与应答器相配合的耦合元件。应答器（如图2）是数据载体，内含一个微型芯片和一个天线线圈组成的耦合元件[1]。

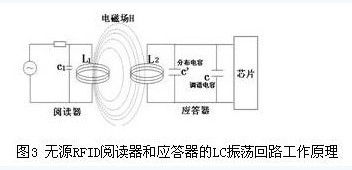
        图3所示为无源RFID阅读器和应答器的LC振荡回路工作原理[2]。阅读器中有由线圈L1电容C1构成的LC振荡回路1，这个振荡回路可以产生频率为f0的交变磁场。应答器中线圈回路的分布电容C’和外接调谐电容C共同构成电容C2与线圈L2并联形成LC振荡回路2，其谐振频率为f，当应答器线圈置于阅读器的交变磁场中并且其谐振频率f与阅读器交变磁场的频率f0相同时，振荡回路1、2产生谐振。谐振使阅读器天线线圈产生非常大的电流，使应答器线圈上的感应电压达到最大值，经二极管整流后作为稳定的电压给微型芯片提供工作所需要的能量，完成阅读器对芯片上的信息读写[3-4]。

        LC振荡回路的频率可根据汤姆逊公式（1）计算得到：

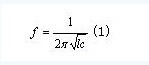
        应答器的谐振频率f是根据所制作的LC振荡回路的电容值C2和电感值L2得到的。

　　应答器的天线线圈可以用金属蚀刻法、金属线缠绕法、真空镀金属法和导电油墨印刷法等多种方法制作得到。线圈生产完成后，其电感值L2就已经确定，根据所测定的线圈电感值L2及阅读器的发送频率f0，可与确定所需匹配的电容值C。由于线圈回路附带了一个分布电容C’，也称为内部寄生电容，而且分布电容C’的值不可测得，所以通过正确合理的方法选择调谐电容C就显得十分重要了。

2、关于调谐电容C的计算

　　如图4所示为笔者用导电油墨印制的应答器线圈，根据阅读器发送频率的要求，所制作的应答器的谐振频率f应为8.2 。通过电感测试仪测得线圈电感的大概值为4.5 。
变换公式1得到：

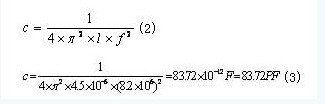
        在标准电容值中选择82PF的电容器帮定到图4所示的线圈导线两端，如图5所示为帮定了82PF电容器的应答器。

        由于在计算中没有虑及线圈的分布电容C’，因此，根据公式（3）计算得到的82PF电容值实际上是应答器中的分布电容C’和调谐电容C的总和。若将82PF作为调谐电容值匹配到线圈上，则线圈的总电容值增大，LC回路中的所得到的谐振频率必定比要求的8.2 小，将不能与阅读器产生谐振，因此必须修正调谐电容值。在修正调谐电容值的过程中要反复的检测修正以后的电子标签的谐振频率，这就需要有专门的仪器来测量电子标签的谐振频率，由于目前还没有用来检测无源电子标签谐振频率的合适的仪器，所以笔者自己设计了一款耦合器，这种耦合器通过实验可以很好的完成检测电子标签谐振频率的工作，下面我们来详细介绍这款耦合器。

3、耦合器的工作原理

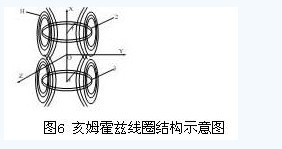
　　耦合器的核心部分是两组围绕在中空圆筒体上的半径为r、匝数为N的线圈2、3，两组线圈平行共轴，中心间距L正好为线圈半径r，从而构成了一个亥姆霍兹线圈[5-6]。如图6所示。

        取L的中心“O”作为空间坐标体系x、y、z轴的中心。产生的磁场分布如图7所示 ：

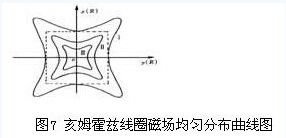
        图7曲线“I”、“II”、“II”内各点的磁感应强度H与中心点的磁感应强度H0的相对误差分别小于1.0%、0.1%和0.01%，中心点0附近的磁场相当均匀，越靠近中心点，磁场均匀性越好。因此，检测无源RFID应答器频率时，把应答器放在亥姆霍兹线圈所产生的磁场空间的中心点O上，以使应答器平面上各点所得到的磁场均匀，磁感应强度几乎相等。

4、耦合器的主要结构

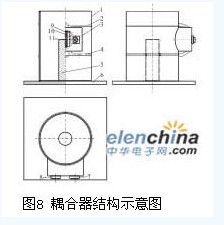
        耦合器结构如图8所示，粘在底座6上的圆柱体1是由1mm厚的硬质塑料板或硬质纸板围成的半径为R的空心筒体。导线2，4分别在筒体1表面绕成紧密相挨的两圈，其垂直距离L等于筒体1的半径R。支撑块3粘在筒体1的外壁上，其内部安装两个BNC接头7、8、变压器铁芯9、两个变压器线圈10、11以及两个调谐电容，圆筒体1中间有圆柱体搁台5用来放置待检测的电子标签。图9（a-d）所示为耦合器实物图。

5、应答器频率测定原理

        与耦合器匹配的频谱分析仪如图10所示，接口1是信号源输出端口，与耦合器的接头7相连，为耦合器提供信号，接口2是信号输入端口，与耦合器的接头8相连，将应答器的谐振信号输入频谱分析仪，根据频谱分析仪屏幕上所显示的感应电压曲线分析应答器的谐振频率。

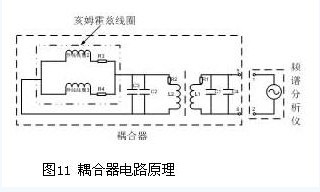
        耦合器电路原理如图11所示。来自频谱分析仪的信号经耦合器内的变压器线圈L1及电容器C1所构成的LC振荡回路1，产生了交变磁场H1。变压器线圈L2及调谐电容器C2、回路分布电容C3共同构成LC振荡回路2，LC振荡回路2受交变磁场H1的作用，产生了感应电流，感应电流通过导线线圈2、3产生频率相同的交变磁场H2。根据亥姆霍兹线圈工作原理，交变磁场H2在耦合器的筒体中心位置产生均匀分布的感应磁场。该感应磁场可以激发放置在其中心位置的应答器使其LC振荡回路产生振荡。

　　当频谱分析仪的扫频频率与应答器的振荡频率相同时产生谐振，应答器回路中的线圈及电容上的电压上升至一峰值。频谱分析仪上所显示的感应电压曲线的峰值所对应的扫描频率即为所测应答器的谐振频率。

　　为了避免耦合器内部的LC振荡回路的振荡频率对待测应答器谐振频率的影响，要求耦合器的自身振荡频率至少在应答器谐振频率的两倍以上。如笔者研制的RFID应答器谐振频率为8.2 ，则为匹配该应答器所研制的耦合器的振荡频率为40 左右。

　　根据汤姆逊公式（1）计算LC振荡频率研制耦合器时，应根据变压器的线圈电感L1、L2值，分别匹配电容。电容值可根据公式（2）计算得到：

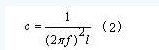
        LC回路1的电容由调谐电容C1与分布电容C4并联构成，LC回路2的电容由调谐电容C2与分布电容C3并联构成，由于分布电容C3、C4很小，耦合器的振荡频率比应答器的谐振频率大得多，根据公式（2）分别计算得到的振荡回路的电容值可近似认为调谐电容C1、C2的值。

6、关于调谐电容C的精确计算

　　为了能够准确计算出能使电子标签产生谐振的调谐电容，必须确定线圈分布电容C’ 的值。因此，笔者必须要测定图5所示应答器的实际频率f实际。

　　利用上述的耦合器来检测我们的印刷出来的电子标签的频率，实验测得：匹配了82PF的调谐电容后，该应答器的实际谐振频率为6.2 ，而不是所要求的8.2 。

　　考虑到用电感测试仪测定的电感值有一定的偏差，所以，用公式（3）计算得到的电容值不是很准确，我们还需要对调谐电容做进一步的匹配，在消除公式（3）中电感测量误差的情况下再计算分布电容。

　　由于分布电容较小，我们先忽略分布电容的值，考虑在实际频率为8.2 的情况下，重新匹配调谐电容C。变换公式（3），得到：

得到： =46.878 PF 。

　　选择51PF的电容器帮定到标签上，测得标签的实际频率为7.3 。因此：分布电容C’的计算可以通过公式（5）得到：

分布电容C’=29.26PF。

　　为了使LC回路得到8.2 的谐振频率，调谐电容C 的计算可以通过公式（6）得到：

计算得到调谐电容 =72.059 PF。

　　选择标准电容值75PF的电容器帮定到LC回路中。经测试LC回路的谐振频率为8.31 ，这是最接近阅读器发送频率的谐振频率。虽然实际匹配的调谐电容值与计算得到的调谐电容值有微小的误差，导致了LC回路谐振频率与阅读器发送频率之间也存在微小的误差。但是由于阅读器的发送频率在一个（f±10%）的扫频范围内，该调谐电容的误差可以得到弥补。

7、结论

　　我们设计的耦合器可以方便地检测无源电子标签的谐振频率，根据反复的检测来计算电子标签的分布电容从而可以计算出我们所需要的调谐电容。频率检测方法实用，准确性高，为无源电子标签的电容和芯片的匹配提供了可靠的依据。