摘 要: 在介绍基本CORDIC" title="CORDIC">CORDIC算法原理的基础上,介绍了其改进的并行算法原理。对并行CORDIC算法进行了详细叙述,并且使用Verilog HDL描述了该算法。通过模块复用,并且采用两相门控时钟等方法,节省了FPGA" title="FPGA">FPGA资源,保持了信号的同步性。最后在Quartus II下进行了综合、仿真,取得了良好的仿真结果。
关键词: CORDIC BBR" title="BBR">BBR MAR" title="MAR">MAR FPGA
CORDIC(Coordinated Rotation Digital Computer),即协调旋转数字计算机,可广泛应用于基本函数的计算,如DSP、FFT、DCT等技术函数的计算。CORDIC算法是Jack Volder于1959年首先提出的。为了扩展可解决的基本函数个数,J.Walter于1971年提出了统一的CORDIC算法(The Unified Cordic Algorithms);2004年,Tso-Bing Juang等又提出了一种改进的并行的CORDIC算法,该改进的算法主要运用BBR(Binary-To-Bipolar Recoding)和MAR(Microrotation Angle Recoding),大大提高了CORDIC算法的迭代速度,并且达到了很高的精度。随着可编程逻辑器件规模的增大和应用范围的扩大,使得利用硬件电路实现该算法成为可能并具有良好的应用价值。
1 CORDIC算法原理
CORDIC算法可分为旋转(rotation)和定向(vectoring)两种方式,还可分为圆形坐标、双曲线坐标和线形坐标三种方式,圆形坐标下旋转方式的原理公式如下:

式中,{xi,yi}和{xi+1,yi+1}分别表示旋转前后的向量,σi∈{-1,1}表示每次旋转的方向。
从公式可知,该运算只有移位和相加(相减)运算。为了获得σi的值,需另设一个变量zi表示每次旋转后的角度与目标角度的差值,然后利用公式zi+1=zi-σi·arctan(2-i)进行计算。根据Jack Volder的推导,经过n次迭代,最终可以得到迭代公式如下:

通过上面的算法介绍可以看出,每次都要先通过计算zi+1和zi才能得到σi的值,这样降低了运算速度。参考文献[3]就是在此基础上,提出了一种提前算出σi的方法,使得速度得以提高。
2 并行CORDIC算法原理
把需要旋转的角度θ范围限定在[-π/4~π/4]之间,并把它分解成下式:

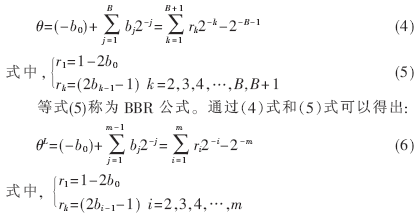



3 利用FPGA实现算法
利用FPGA实现算法时,采用32位精度,即B=32。根据m计算公式可以计算出m=11。根据输入的θ值和公式(6),可以计算出前11个σ值。根据已经计算出的表1可得出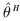 。
。

再根据公式(8),(9)计算出剩下的σ值。经过移位器,加法器最终可以得到旋转后的向量坐标。
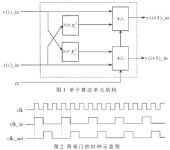
根据上述原理,需要移位40次。所以可通过反复调用图1所示的模块来节约资源。
对于本算法,第i+1个模块的输入为第i个模块的输出,因此,对模块的工作时序有一定的要求。针对FPGA中寄存器资源较为丰富的特点,在上述模块的输入输出端分别加入寄存器,对输入和输出进行锁存;使用两个进程描述移位加法和控制信号,并且使用不同的时钟信号作为敏感信号;为了保持整个设计的同步性,又采用了两相门控时钟进行控制(如图2所示)。图中clk_in作为输入寄存器的时钟,而clk_out作为输出寄存器的时钟。
两相门控时钟生成的相关程序如下:
always @(cnt)
begin
case (cnt)
2′d0: {clk_out,clk_in}=2′b01;
2′d1: {clk_out,clk_in}=2′b10;
2′d2: {clk_out,clk_in}=2′b00;
default:{clk_out,clk_in}=2′b00;
endcase
end
4 仿真结果
本文在Quartus II环境下对利用Verilog编写的RTL代码进行了综合,使用了115个LAB。由于在一片FPGA芯片中可集成其他相关模块,在系统设计中具有良好的应用价值。对其进行时序分析,本设计可达到的最大时钟为58MHz,满足高速系统设计的要求。
图3是在Quartus II下以初始角度0度、旋转角度30度为例的一个仿真结果,经过118个时钟周期后可以得到旋转后的正弦值和余弦值。
通过理论分析及仿真实验结果可以看出,这种新的并行CORDIC算法在FPGA上实现具有可行性。算法中旋转方向的优先判断,使得运算速度大大提高。与以往在FPGA上实现原始的CORDIC算法相比,具有更高的速度和准确性。
参考文献
1 JACK E.VOLDER.The CORDIC Trigonometric Computing Technique. IRE Trans.ElectronicComputing,1959; EC-8:330~334
2 J.Walther. A unified algorithm for elementary functions.Spring Joint Computer Conf.,1971:379~385
3 Tso-Bing Juang,Shen-Fu,Ming-Yu Tsai.Para-CORDIC: Parallel CORDIC Rotation Algorithm. IEEE,2004;51(8)
4 J.Bhasker(著),孙海平(译).Verilog 综合实用教程.北京:清华大学出版社,2004
5 Uwe Meyer-Baese(著),刘 凌,胡永生(译). 数字信号处理的FPGA实现[M]. 北京:清华大学出版社,2003:55~63