在运输中如何进行货物的有效装载，即怎样将一批矩形货物布入一个或多个集装箱中，使集装箱的空间利用率达到最高，这属于NP完全问题。集装箱装载问题根据集装箱数量的有限和无限划分成两类：一是集装箱数量无限，盒子必须全部装完，要使所用的集装箱数量最少；二是集装箱数量有限，盒子数量超过了集装箱的装载能力，要求被装载盒子的总体积达到最大，使空间利用率最高。在实际中第二类问题更为常见，所以在此只分析第二类问题。
　　目前常用的布局优化方法多为不带约束的简化布局问题，而现实生活中存在着大量的约束条件。
　　针对具有货物底置位置、允许侧放方式、最大堆码层数等多约束条件下的集装箱装载问题和目前集装箱容积有效利用率普遍较低的情况，本文将这些约束考虑到启发式规则中，根据装载中单种货物数量一般较多的实际情况，提出了一种新的基于空间划分的启发式算法，并将其与遗传算法结合，进一步提出了混合遗传算法求解多约束装箱问题。该算法已用于企业的实际装箱中，结果表明，本文提出的方法可行且有效。
1 多约束集装箱装载的启发式策略
　　实际装载中单种货物数量一般较多，采用现有针对单个物品的基于三维空间的启发式算法存在装载效率和空间利用率低的问题。因此，本文采用同类型货物一次性装载的思想，提出了一种新的基于空间划分的启发式策略。该策略根据待布局空间块中货物装载方式的不同将剩余空间最多划分为五种空间块。实际应用中，对算法中的约束条件处理方法是引入不同变量分别表示货物的侧放方式、货物的堆码层数、底置等级等属性。
1.1 基于空间划分的启发式算法流程
　　算法流程的步骤如下：
　　(1)初始化空间块序列为集装箱箱体。
　　(2)依次按底置等级递增、体积递减对货物类型排序。
　　(3)从货物类型序列中按顺序取某类型货物，从空间块列表中取第一个" title="第一个">第一个可用空间块。
　　(4)将所取类型的货物一次性装载到所取空间块中。根据货物可取侧放方式、最大堆码层数的不同，计算空间块的最大装载数量(本文称为标准装车)，同时产生标准装车的摆放方式。当货物数量小于标准装车时(称为非标准装车)，根据货物数量、允许侧放方式、最大堆码层数产生非标准装车的摆放方式。
　　(5)分割空间块，将其添加到空间块序列，按体积对空间块重新排序。
　　(6)如(4)为标准装车，求所取类型货物的剩余数量，从空间块列表中取第一个可用空间块，转(4)；否则转(3)。
1.2 定序" title="定序">定序规则
　　定序规则用来确定物体布入的先后顺序，对最终布局结果的优劣有重要影响。由于货物底置等级越低，要求放置的位置越低，所以采用依次按底置等级递增、体积递减的定序规则对货物类型排序。

1.3 定位规则
1.3.1 标准装车
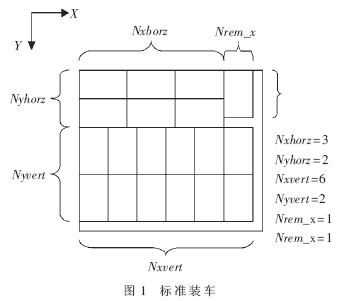
　　装车规则：对箱体的某种侧放方式，X-Y平面的摆放次序为先横后纵。如图1所示，Nxhorz，Nyhorz，Nyvert，Nxbert分别表示整的横箱、纵箱在X轴和Y轴的数目；Nrem_x，Nrem_y表示零头在X轴和Y轴方向的数目；wid表示待布局立方体的宽。确定Nyhorz和Nyvert满足：
　　min{wid-Nyhorz×boxwid-Nyvert×boxlen}　　　　　　(1)
　　零头应置于最外侧。零头的摆放应考虑空间完整程度, 再决定横放还是纵放。如果程度一致，则横放。在Z轴方向，根据货物可取侧放方式、最大堆码层数遍历得到最优的箱子层数lay_num和各层的侧放方式。最优判定准则是可装的箱子数目最多。
1.3.2 非标准装车
　　装车规则：当装载不满时：(1)应避免中间突出的情况，以免使空间过于破碎。如有中间突出的情况，应把突出的摆放换到边上，这样可以利用最外边的一段空间。(2)如有小于最小尺寸的边，应尽量把此类情况转换为其他方式。(3)在宽度方向上求最优，是为了维护空间完整度。
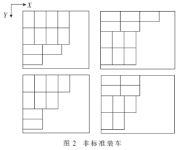
　　非标准装车有以下几种情况，如图2所示。

　　设待布局箱子数目为num_all，如空间块的标准装车方式所确定的各层侧放方式不同，则首先根据标准装车摆放各层，对不满的一层，令lay_num=1，刷新num_all，转(1)。
　　如标准装车方式所确定的各层侧放方式相同，则：
　　(1)由标准装车确定的各参数计算箱体在所布空间块的理论长度La，其中：
　　La=Va/(Nyhorz×boxwid+Nyvert×boxlen)　　　　　　(2)
　　Va=boxwid×boxlen×num_all/lay_num　　　　　　　(3)
　　(2)计算纵放排数：Nxvert1=La/boxwid　　　　　　　(4)
　　横放排数：Nxhorz1=La/boxlen　　　　　　　　　　　(5)
　　(3)计算余箱数
　　num_r=num_all-Nxvert1×Nyvert-Nxhorz1×Nyhorz　　　(6)
　　(4)余箱放置的种类有以下几种：V0表示竖放；H0表示横放；V1表示竖放1列或几列，其余按横放；H1表示横放1列或几列，其余按竖放。

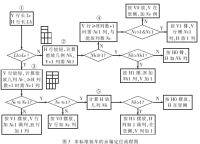
　　这4种方式对应的共同约束为：所有情况的最长行不能超过长度界限；优先级应考虑空间的完整性和较短的总长度。具体流程如图3所示。图3中各公式如下：
　　①Lv=trunc(La/boxwid)
　　　Lh=trunc(La/boxlen)
　　②Nh=num_r/Nyhorz
　　　Nh1=(Lv+boxwid-Lh)/boxlen
　　③Nv=num_r/Nyvert
　　　Nv1=(Lh+boxlen-Lv)/boxwid
　　④同③

1.4 空间划分
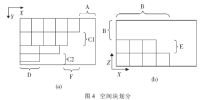
　　空间块的划分如图4(a)、(b)所示。根据零头所在位置的不同，空间块可最多分割为A-B-C1-D-E-F或A-B-C2-D-E-F五种，各空间块可视化时的遮挡顺序为D-E-C-F-B-A。
2 约束集装箱装载问题的混合遗传算法
　　采用以上基于空间划分的启发式算法的效率较高，但仍然难以保证获得全局最优解或次优解。遗传算法^[4]作为一种模拟自然进化过程的随机性全局优化概率搜索算法，在求解优化问题中显示了优越的性能。因此本文将启发式算法与遗传算法结合，进一步提出了求解多约束装箱问题的混合遗传算法。
2.1 染色体的编码方法
　　编码是GA应用成功与否的关键。本文采用Grefen-
　　stette等针对TSP提出的基于顺序表示的遗传基因编码方式^[4]，把待装物品的类型编号按排放顺序排的串作为一个解的编码，即p={p₁，p₂……p_n}。其中n表示装物品的类型；p1为整数，其值代表物品类型的编号。
2.2 目标函数和适应度
　　在集装箱装载过程中不仅要求容器空间利用率达到最高，同时要考虑多种约束。由于在启发式装载过程中引入了不同变量(暂不考虑重心约束)，因此适应度函数为：