自动消除DSA图像中运动伪影的方法
2008-07-01
作者:李 雯,聂生东
摘 要: 在数字减影血管造影技术中,病人的移动常会造成图像上出现伪影,干扰医生的正常诊断。提出一种基于图像配准思想的全自动消除伪影的方法,选择合适的控制点和相应的相似性测度,并结合三次样条插值" title="插值">插值方法。实验证明,该方法能够在亚像素" title="亚像素">亚像素水平自动消除DSA图像中的运动伪影,是一种快速有效的方法。
关键词: 数字减影血管造影 运动伪影 配准
通常,造影剂注入前的DSA血管图像被称为蒙片(Mask Image),而同一部位在注入造影剂后的X射线图像被称为活片(Live Image)。在假设血管周围组织、成像条件完全不变的情况下,将蒙片与活片相减应得到仅包含血管的图像。但在临床应用中,这种理论假设总是不成立的。在成像的同时,病人会有各种运动,其中有些运动是不可避免的,如呼吸、肌肉运动、心脏运动以及在造影剂注入时由于病人的自然反应而引起的局部运动等。这些运动会使活片与蒙片之间存在并非由造影剂造成的差异,从而使减影后的图像出现伪影,妨碍医生的正确诊断。本文提出了一种自动消除数字减影血管造影DSA(Digital Subtraction Angiography)减影图像中伪影的方法。通过实验证实,本方法比其他类似的方法[1]更快、更有效。
1 方法原理
DSA序列图像的配准目的是通过图像处理和图像分析手段找到一种几何变换方法能消除序列图像中任意二幅之间因为病人的运动带来的伪影。本文选择对蒙片作相应的变形(warping),使其在图像相减之前与造影图像相匹配。
DSA图像的实质就是X射线投影图像。根据不同物质对X射线的吸收系数的不同,在三维空间把沿着射线方向的不同物体的吸收系数叠加,形成二维投影图像。因此,DSA图像中的运动伪影是由三维空间运动造成的。
2 实现过程
配准的具体过程为:首先,对于一幅图像中的某一点,根据一定的相似度函数找到另一幅图像中的对应点,并求出" title="求出">求出相对位移;然后对其中一幅图像(蒙片)进行变形,以达到与另一幅图像(活片)配准的目的。但如果分别计算每一点的位移,则计算量太大,不能满足临床要求。因此可以先求少数特征点(控制点)的位移,再通过插值方法得到所有点的位移,以此得到快速配准的方法。下面介绍具体算法。
2.1 找控制点
控制点的选取有多种方法,如用人工方法选取感兴趣区域中的某些点,或者在图像中用规则的网格选取等。经观察,大多数运动伪影出现在图像的边缘点上,因此可以认为边缘点的匹配比均匀区域的匹配更可靠,选择用边缘点作为控制点。
通过边缘检测" title="边缘检测">边缘检测算子可以找到图像的边缘点。边缘检测方法很多,本文选用Canny边缘检测。它是一种比较新的检测算子[2],具有很好的边缘检测性能,正得到越来越广泛的应用。Canny边缘检测法利用高斯函数的一阶微分,能在噪声抑制和边缘检测之间取得较好的平衡。由于没必要把所有用Canny算子检测出的点都作为控制点,所以在Canny边缘点计算出该点的梯度值后,根据阈值来判断该点是否作为控制点。
为使控制点的分布更合理,利用比例因子对控制点间的距离作规定:每2个控制点间的最小距离为Dmin=λminM。同时为避免在很大区域内没有控制点,也规定控制点间的最大" title="最大">最大距离:Dmax=λmaxM。通常在DSA图像中,有用的信息都显示在一个圆形区域内,区域之外的像素值为零。这样的圆形区域被称为“曝光区域”,其定义如下:
R=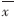 (x-xc)2+(y-yc)2≤r2,Xmin≤x≤Xmax,Ymin≤y≤Ymax
(x-xc)2+(y-yc)2≤r2,Xmin≤x≤Xmax,Ymin≤y≤Ymax
其中,(xc,yc)为影像增强器的中心点,通过适当校正可与图像的中心点重合。r为圆形区域的半径,而Xmin、Xmax、Ymin、Ymax分别是图像的左、右和上、下边界。既然所有有用信息都在圆形区域内,因此控制点也应该在R之内寻找。
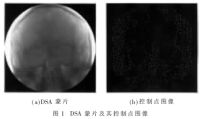
图1为DSA蒙片及其控制点图像,其中图1(a)为一脑部DSA正面图像的蒙片,图1(b)是从图1(a)中得到的控制点图像。由图可见,控制点都位于边缘上,且保持着一定的均匀度。
2.2 选择相似性测度
本文采用模版匹配法求蒙片与活片中像素的相对位移: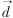 =(dx,dy)。模版匹配法利用相似性测度来求一幅图像I0(x,y,t0)中的某一点P(x,y)相对于另一幅图像I1(x,y,t1)(t1>t0)的位移,以P点为中心,以I0中P点周围W×W邻域内的点为一窗口,在I1中求出这一邻域移动
=(dx,dy)。模版匹配法利用相似性测度来求一幅图像I0(x,y,t0)中的某一点P(x,y)相对于另一幅图像I1(x,y,t1)(t1>t0)的位移,以P点为中心,以I0中P点周围W×W邻域内的点为一窗口,在I1中求出这一邻域移动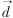 后的窗口位置,并利用适当的相似性测度,求出使相似性测度达到最大的位移,即为要求的最佳位移。
后的窗口位置,并利用适当的相似性测度,求出使相似性测度达到最大的位移,即为要求的最佳位移。
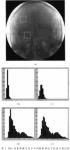
本文选用基于图像直方图的相似性测度[3],当两幅图达到最佳匹配时,两幅图像之差的直方图会集中在很窄的一段灰度范围内,且形成明显的峰值,而当两幅图像不是很匹配时,直方图的集中程度会降低;更重要的是,直方图的这种性质不会受血管的影响,DSA造影图像及其在不同配准情况下的直方图比较如图2所示。其中图2(a)是DSA造影图像,其中的白框表示被选取的区域,左上方的白框不包括血管,而中间的白框包括血管;图2(b)和图2(c)分别表示不包括血管时,最佳和非最佳配准下差异图像的直方图;图2(d)和图2(e)分别表示包括血管时,最佳和非最佳配准下差异图像的直方图。
假设待配准的两幅图像分别为I0(x,y,t0)和I1(x,y,t1)(t1>t0),求I0中某一点P0的位移。在P0周围选取一个小窗口W0,该窗以P0为中心,大小为W×W个像素,对于每一个位移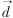 在I1中找到相应的相同大小的窗口W1,将这两个窗口相减,得到差异图像Wd(W×W),针对Wd计算相似性测度,有研究人员提出基于直方图的判定标准[3]:
在I1中找到相应的相同大小的窗口W1,将这两个窗口相减,得到差异图像Wd(W×W),针对Wd计算相似性测度,有研究人员提出基于直方图的判定标准[3]:

其中[δmin,δmax]?奂Z是差异图像中可能的灰度范围,h(δ)是差异图像的归一化直方图![]() ,并假设f是严格凸函数或严格凹函数,但可微。相关文献提出了多种基于直方图的f函数形式[4],并指出当f(x)=x2时计算简单且精度高。这样,式(1)应写成:
,并假设f是严格凸函数或严格凹函数,但可微。相关文献提出了多种基于直方图的f函数形式[4],并指出当f(x)=x2时计算简单且精度高。这样,式(1)应写成:
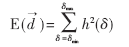
2.3 亚像素精度
某些研究者指出,即使是亚像素级的移动也会造成两幅图像间的差异很大[5],因此在计算像素位移时应设法达到亚像素精度,而这要用到图像插值技术。本方法通过先对图像插值和重采样,然后对插值后的图像求相似性测度来达到亚像素精度。期望达到的亚像素精度为0.1 pixel。
图像插值在整个配准算法中很重要。它的精度直接影响着位移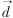 的精度;它的计算速度影响着整个算法的计算时间。如何选择一种既精确又快速的插值方法成为此配准算法成败的关键。本文采用三次多项式插值法对原图像I0进行插值。为得到理想的效果,本文采用4×4的卷积核。
的精度;它的计算速度影响着整个算法的计算时间。如何选择一种既精确又快速的插值方法成为此配准算法成败的关键。本文采用三次多项式插值法对原图像I0进行插值。为得到理想的效果,本文采用4×4的卷积核。
2.4 最优化搜索
在确定了相似性测度为直方图能量E(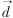 )后,要求最佳位移
)后,要求最佳位移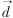 使相似性测度达到最大。本问题属于无约束优化问题,针对该问题,本文采用直接搜索法。最常用的是鲍威尔(Powell)法[6]和单纯形法。这里采用鲍威尔法,也称为方向加速法。
使相似性测度达到最大。本问题属于无约束优化问题,针对该问题,本文采用直接搜索法。最常用的是鲍威尔(Powell)法[6]和单纯形法。这里采用鲍威尔法,也称为方向加速法。
搜索的速度受计算位移时选用的窗W×W大小影响显著,这是个矛盾的统一体:一方面为了减少搜索时间,希望采用较小的窗;另一方面,较小的窗将使相似性测度产生许多局部极大点,导致搜索结果不可靠。因此在选择窗的大小时应该慎重考虑,本文选用的窗口大小为51×51个像素。
2.5 位移插值
求出所有控制点的最佳位移后,进而需要求出图像I0中所有点相对I1的位移,这要利用线性插值来估算出所有点的位移。本文采用Delaunay三角插值法[7],它保证在每一个三角形内的最小角度尽可能地最大化,且保证了这种三角形分法的惟一性。
获得图像I0中所有点的位移后,即可对图像I0进行校正。因为位移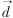 的单位是0.1像素,则图像上一点根据
的单位是0.1像素,则图像上一点根据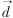 移动后极可能落入整数值的网格之间,这里需要用插值法(双线性插值)得到非整数像素位置上的像素值。
移动后极可能落入整数值的网格之间,这里需要用插值法(双线性插值)得到非整数像素位置上的像素值。
3 实验结果及讨论
拍摄后前位的DSA时间序列图像共39幅,每幅图像的大小为512×512个像素,选取其中的第1幅(蒙片)和第28幅(活片)作DSA图像的配准研究,其中的蒙片如图1(a)。
控制点提取之后(见图1(b)),根据模板匹配法计算每个控制点的最佳位移,亦即使差异图像的直方图能量达到最大时的位移。此时,对窗口大小W的选择很重要。若采用鲍威尔最优化方法搜寻最佳位移,则要求E(d)足够光滑以至于只有一个极值。窗口太小将增加E(d)的局部极小值,从而影响到最优解的精度。经多次尝试和比较,选用的窗口大小为51×51个像素。
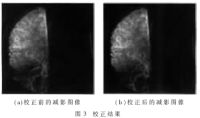
校正结果如图3所示,其中图3(a)是校正前蒙片与活片直接减影后的图像,而图3(b)是经过校正后再做减影的图像。从结果看,使用本方法能去除减影图像中的大部分伪影。在同一台计算机上(奔腾4处理器,512MB内存),先后采用本文提到的方法和文献[1]中的方法处理图3(a)。比较得出,虽然最后的校正效果差不多,但本方法所用的时间仅为另一种方法的三分之一。由此可看出,本文提出的关于自动消除DSA图像中的运动伪影的方法,是快速、有效的。
参考文献
1 周宗恒,李 炜,曹津升.基于图像特征配准的数字血管减影算法.计算机工程与应用,2001;37(23):169~171
2 Canny J F.A computational approach to edge detection.IEEE Transactions on Pattern Analysis and Machine Intelli-gence,1986;8(6):679~698
3 Buzug T M,Weese J,Fassnacht C et al.Image registration:convex weighting functions for histogram-based similarity Measures.Lecture Notes in Computer Science,Springer-Ver-lag,Berlin,1997;1205:203~212
4 Buzug T M,Weese J.Image registration for DSA quality enhancement.Computer Med Imaging Graphic,1998;22(2):103~113
5 Brody W R,Enzmann D R,Deutsch L S.Intravenous carotid arteriography using line-scanned digital radiography.Radi-ology,1981;139(2):297~300
6 Powell M J D.An efficient method for finding the minimum of a function of several variables without calculating derivatives.Computer Journal,1964;7(2):155~162
7 Flusser J.An adaptive method for image registration.Pattern Recognition,1992;25(1):45~54