摘 要： 提出了一种基于LTS Hausdorff距离与遗传算法" title="遗传算法">遗传算法的图像配准" title="图像配准">图像配准方法。算法首先对参考图像和待配准图像进行压缩、二值化" title="二值化">二值化和边缘检测" title="边缘检测">边缘检测预处理，然后在此基础上结合遗传算法对待配准图像进行配准操作。
    关键词： 图像配准  遗传算法  LTS Hausdorff距离  边缘检测  二值化

    图像配准是图像处理" title="图像处理">图像处理的基本任务之一，它的主要作用是将不同时间、不同传感器、不同视角及不同拍摄条件下获取的两幅或多幅图像进行匹配(主要是几何意义上的)。近年来，对图像配准技术的研究涵盖了多个应用领域，在计算机视觉、模式化识别、医学图像分析和遥感数据处理等学科中，图像配准技术均占有举足轻重的地位，图像配准己成为很多研究课题的必备环节。
    图像配准中的一个关键问题是如何利用一种行之有效的方法来评价图像间的相似程度。自1991年Daniel P.Huttenlocher与William J.Rucklidge等人提出了一种基于Hausdorff距离的计算图像间的相似度的方法^[1]后，Hausdorff距离作为一种评价两个图形位置关系的量化标准已被大量应用到图像配准的研究领域中，其良好的配准精度也被大量的实验和研究所证明。尽管在图像配准中，单纯的Hausdorff距离计算上存在一个比较大的缺点，即对于噪声和孤立点的敏感性，但由Hausdorrff距离改进的LTS（Least Trimmed Square）Hausdorff距离却可以很好地克服这些问题，因此作为一种改进方法，LTS Hausdorff距离在数字图像的配准中的精确度与稳定性都比较理想。
    作为一种有效而且实用的优化算法——遗传算法在很多方面得到了应用。在图像处理方面，Chalermwat、Ghazawi等人将遗传算法应用于图像的配准；而Brumby、Theiler等人则利用遗传算法进行图像的特征提取。从他们的实验结果来看，遗传算法在图像处理方面具有很好的优化效果。
    本文首先将参考图像与待配准的图像进行预处理（图像的压缩、二值化和特征提取），以避免在计算Hausdorff距离时产生过大的代价，然后在此基础上结合遗传算法对待配准图像进行配准操作（平移、旋转、幅度变换），最终的目的是通过遗传算法搜索到最优的平移、旋转和幅度变换参数。实验表明，这种方法可以有效地抵抗在配准的过程中产生的噪声和孤立点的影响，并且在保证一定的配准精度的前提下可以提高配准的效率，算法的健壮性良好。
1 算法的基本原理
1.1 Hausdorff距离及其改进
    Hausdorff距离是一种极大极小距离，它主要用于测量两个点集的匹配程度。Hausdorff距离的引入使物体匹配基于一种新的测度，它能更为有效地表征物体轮廓边缘之间的相似度。
    给定两个点集A={a₁，a₂，…，a_p}和B={b₁，b₂，…，b_p}，则A、B之间的Hausdorff距离定义如下^[2]：
    H(A,B)=max(h(A,B),h(B,A))
    式中，称为前向的Hausdorff距离，称为后向的Hausdorff距离，||·||为定义在点集A和B上的某种距离范式，本文使用的是L2范式(欧式距离)。对于任何两个点集A、B，若H(A，B)=d，则表明对于任何点a∈A，与B中的任何点b∈B的距离必定不会超过d，而且反过来对于B也是成立的。因此，Hausdorff距离可以有效地衡量两个点集(尤其是几何图形)间的位置关系，但是在图像处理的实际应用中原始的Hausdorff距离在计算的过程中存在一个比较大的缺点，即对噪声和孤立点的敏感，这个缺点严重影响了图像配准的整体准确性和算法的健壮性。为了克服这一缺点，本文使用的是Hausdorff距离的改进形式——LTS Hausdorff距离^[3]：
   
    式中，H=h×N_A，N_A为A中的点的个数，h∈[0.6，0.9]，dB(a)(i)表示在从点a到B集合中每个点的距离中第i大的值。由公式可以看出，LTS Hausdorff距离取的并不是最小距离中的最大值，而是用一种排序再求部分均值的方法来确定A、B之间的距离，从而在很大程度上减小了噪声和孤立点对精度和稳定性的影响。
1.2 遗传算法
    遗传算法(GA)作为一种求解全局最优化的方法，在许多领域的理论与工程实践中都有成功的应用。其主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不依赖于梯度的信息^[4]。
    遗传算法使用所谓的遗传算子（genetic operators）作用于群体P(t)中，进行下述的遗传操作，从而得到新一代群体P(t+1)。
    (1)选择(selection)：根据每个个体的适应度，按照一定的规则或方法，从第t代群体P(t)中选择出一些优良的个体遗传到下一代群体P(t+1)。
    (2)交叉(crossover)：将群体P(t)内的每个个体随即搭配成对，对每一对个体，以某个概率（称为交叉概率(crossover rate）)交换它们之间的部分染色体。
    (3)变异（mutation）：对群体P(t)中的每一个个体，以某一概率（称为变异概率(mutation rate）)改变某一个或某一些基因坐上的基因值为其他的等位基因。
2 算法的实现
    本文所提出的图像配准算法的主要思路是：首先对图像进行预处理，然后在一定的范围内，通过遗传算法搜索图像配准的最佳变化参数(角度变换量α、X轴平移量α、Y轴平移量y及幅度变换量s）。在遗传算法的执行过程中，利用LTS Hausdorff距离作为遗传算法的适应度函数，来判别每一代种群中的个体的好坏，然后可以确定哪些变换可以保留到下一代继续进行遗传操作，最后当遗传算法停止的时候，就可以确定最优的变换参数。
2.1 算法的实现流程
    在整个配准过程开始之前，首先要对参考图像和待配准图像进行预处理，预处理主要包括：对图像的压缩、二值化和边缘检测。对图像的压缩主要是为了在保证一定精度的前提下减少计算过程的代价，之后的二值化本文主要采用自适应的阈值分割算法，最后的边缘检测的目的主要是提取图像中的特征，通过对两幅图像特征的配准可以进一步地减少算法的复杂度。 本文使用的“canny”算子的边缘检测算法，最后就是对预处理过的图像进行具体的遗传算法的图像配准的操作。算法的实现流程图如图1所示。

               
2.2 遗传算法的个体编码
    编码是应用遗传算法时要解决的一个首要问题，而且也是设计遗传算法的一个关键步骤。编码的方法除了决定个体的染色体排列形式外，还决定了个体从搜索空间的基因型变换到解空间的表现型时的解码过程，同时也影响了交叉和变异操作。遗传算法的编码方法很多，其中二进制编码是最基本也是最常用的方法，但是在图像配准中二进制编码存在着比较大的缺点：由于配准的图像尺寸可能不同，所以二进制编码的位数无法事先确定，若图像的尺寸改变了，可能就要修改染色体中编码的位数来适应不同的解空间，因此本文采用的是实数编码。本文要搜索的变换参数包括X轴平移距离x、Y轴平移距离y、旋转角度?琢及尺寸变换s。可以把这些参数定义为一个四元组（x、y、α、s），并采用实数编码的方式对这个四元组进行编码，然后作为遗传算法中的个体的样本。
2.3 遗传算法所选取的适应度函数
    在整个配准的过程中，核心问题是必须有一个合适的个体评价函数作为适应度函数。所谓的个体评价函数就是两幅图像的相似性的量度，本文是以LTS Hausdorff距离作为评价两幅图像间相似程度的评价函数，并作为遗传算法中个体的适度函数应用到遗传算法的具体操作中。适度函数如下：
   
式中，t是遗传算法的代数，i是第t代中的第i个个体，R代表的是经过了预处理后的参考图像，而M_i代表在第t代的遗传操作中的第i个个体的待配准图像。
2.4 遗传算法的选择机制及交叉概率和变异概率
    在确定了编码方法和适度函数后，整个算法的重点就转移到遗传算法的细节上，其中一个比较重要的问题是选择机制的确定。选择是遗传操作的一部分，其任务是参照适度函数的标准按照一定的选择机制来保留优势个体，淘汰劣质的个体。本文采用的是适应度比例与最佳个体保存相结合的选择机制，设群体大小为n，其中个体i的适应度为F_i，按照适应度比例方法，个体i被选中的概率为：
   
    交叉概率和变异概率的确定应满足的原则是：一方面能保证个体的多样性，防止过早的收敛；另一方面又不会使算法过渡发散。针对本文的具体配准问题和算法，经过反复实验测试，本文确定的交叉概率PC=0.8，变异概率PM=0.07。
3 实验结果
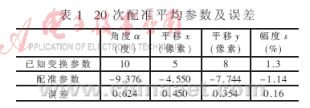
    本文所有实验都是在Matlab7.1环境下完成的，运行实验的计算机配置是：P4 1.8G、512MB内存。实验选取了两幅医学图像，其中作为参考图像的是一位病人脑部的某一层面的MIR图，如图2(a)所示。而待配准图像是该病人脑部同一层面的PET图，如图2(b)所示，两幅图像的原始尺寸是512×512像素。经过预处理后的两幅图像分别如图2(c)、图2(d)所示。图2(e)是经过配准后的PET图，图2(f)是配准后的PET图与MRI图的对比效果。经过20次配准后得到的数据的平均误差如表1所示。
                    

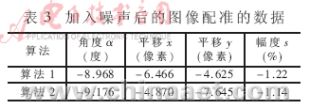
    使用不同的算法对以上的图像配准后的配准变换数据对比分别如表2、表3所示。表2是原始的参考图像和待配准的图像分别经过两种算法配准后的数据，表3是两幅图像分别加入噪声后分别经过两种算法配准后的数据。其中算法1是“原始的Hausdorff距离结合遗传算法的配准”，算法2是“LTS Hausdorff距离结合遗传算法的配准”。由表2、表3数据可以看出，当图像的质量比较好时，用两种算法配准后的数据非常地相似，但是一旦图像中的噪声比较明显时，算法1的数据前后变化就比较大，这就证明了基于原始的Hausdorff距离的遗传算法配准受图像的噪声和孤立点的影响比较大，算法的健壮性不好；而算法2的数据在表2和表3中的变化不是很明显，说明了LTS Hausdorff距离结合遗产算法的图像配准算法的稳定性较好。

                         
    本文提出的图像配准方法，通过遗传算法结合LTS Hausdorff距离实现两幅不同模态的医学图像的配准。为了避免在计算距离时产生太大的代价，笔者首先通过压缩图像和边缘检测的方法对原始图像进行预处理，提取出配准所需的特征图像；然后利用LTS Hausdorff距离作为适度函数的标准，再使用遗传算法搜索配准的最优变换参数。试验证明，本文提出的算法可以满足一定的配准精度要求，而且健壮性也比较好。
参考文献
[1] HUTTENLOCHER D P，KLANDERMAN G，RUCKLIDGE W J.Comparing images using the hausdorff distance.IEEE Transactions on Pattern Analysis and Machine Intelligence[J]，1993，(15)：850-863.
[2] HUTTENLOCHER D P，RUCKLIDGE W J.A multi-resolution technique for comparing images using the Hausdorff distance.IEEE Transactions un Pattern Analysis and Machine Intelligence[J]，1993,(14)：705-706.
[3] SIM D G，KWON O K，PARK R H.Object matching algorithms using robust hausdorff distance measures.IEEE Transactions On Image Processing[J]，2004，15(3)：425-428.
[4] HOLLAND J H.Adaptation in natural and artificial system[M].Ann Arbor：University of Michigan Press，1975：30-58.