摘 要： 介绍一种新的多尺度分析" title="多尺度分析">多尺度分析方法，并给出了一维EMD实现方法及其在信号处理中的应用以及二维EMD实现方法及其在图像处理" title="图像处理">图像处理中应用，该方法的应用实例及分析过程，同时分析了EMD的优越性和应用前景。
    关键词： HHT  多尺度分析  EMD

    自然界的绝大多数现象都是非线性、非平稳又或者伴有非线性、非平稳现象的过程，因而在信号分析" title="信号分析">信号分析中，非平稳信号分析是重要而常见的，以往对它们的处理方法都或多或少存在缺点和不足^[1]。希尔伯特-黄变换HHT(Hilbert-Huang Transform)是继小波变换之后,由美国科学家Norden E Huang等人于1998年提出的又一种多尺度分析的全新方法。是一种适合处理非线性，非平稳信号的分析方法。非线性、非平稳信号分析的主要目的是要揭示信号时频变化规律。这种规律虽然目前可以通过短时傅立叶变换、小波变换等时频分析法进行分析，但这些方法都是通过幅值谱来展示频率变化规律的，实质都是以傅立叶变换(FT)为理论依据，因此不可避免地会因FT分析非线性、非平稳信号所带来的缺陷，如出现虚假频率，因此所显示的信号的频率变化规律只能是粗略的。此外，小波变换作为近年来广泛受到关注和应用的多尺度分析方法也存在不能克服的缺陷，如最优小波基的选取、变换层数的确定，在不同小波基下处理所得的结果大不相同。正是在这一背景下，N.E.Huang等人创造性地提出了固有模态函数IMF(Intrinsic Mode Function)概念和经验模式分解EMD(Empirical Mode Decomposition)方法，再将信号分解所得的各阶IMF进行Hilbert变换，形成时间频率能量谱，从而得到瞬时频率并定义为Hilbert谱。美国NASA宇航中心将这种形式的Hilbert变换称为Hilbert-Huang变换（HHT）。这是一种以瞬时频率为核心概念的方法，理论上能精确给出信号中频率随时间变化的规律，避免了虚假频率等冗余现象，同时EMD的基随信号自适应地产生，不同信号的基是惟一的，不需要选择。HHT方法一出现就受到广大研究人员的青睐。现已应用到地球物理、生物医学、振动工程、机械工程、故障检测、图像处理等领域，实践表明，较依赖于先验函数基的Fourier分析和小波分析等方法，HHT更适合处理非平稳信号，是一种具有自适应性的时频局部化多尺度分析方法。将Nunes等人的一维EMD思想应用于二维图像处理中，使EMD的发展向前迈进了一步。本文给出了二维EMD的实现方法及应用。
1 EMD的实现及应用
1.1 一维EMD和Hilbert的实现
    Hilbert-Huang变换分为两步：首先用经验模态分解方法EMD获得有限数目的固有模态函数IMF，然后再利用Hilbert变换和瞬时频率方法获得信号的时-频谱——Hilbert谱。由于瞬时频率方法对任意信号不都适用, 它只对单分量信号(Monocomponent signal)才有意义，而对于自然界和工程应用领域，获取的信号一般都不能满足单分量信号的要求，因此，必须对信号进行适当的处理。经验模态分解方法(EMD)就是通过对信号进行分解，使之能够表示为许多单分量信号之和。在Hilbert-Huang变换中，为了把复杂的信号分解为简单的单分量信号的组合, EMD所获得的固有模态函数(IMF)必须满足下列两个条件^[2-3]：
    (1)在整个信号长度上，一个IMF的极值点和过零点数目必须相等或至多只相差一点。
    (2)在任意时刻，由极大值点定义的上包络线和由极小值点定义的下包络线的平均值为零，也就是说，IMF 的上下包络线对称于时间轴。满足上述条件的IMF就是一个单分量信号。对于给定的信号，Huang所介绍的EMD方法是：
    首先找到信号的极大值和极小值，通过三次样条拟合，从而获得信号的上包络曲线env_max和下包络曲线env_min, 计算上下包络曲线的平均值曲线m1：m1=(env_max+env_min)/2。设分析信号为x(t)，则：
    x(t)-m₁=h₁
    从理论上讲，h₁即为第一阶IMF分量，但由于样条拟合h₁不一定满足IMF的条件，因此把h₁作为原始数据，重复上述步骤，反复减均，直到满足IMF的条件为止。然后，从原始信号中减去h₁即可获得信号的逼近分量R₁。
    x(t)-h₁=R₁
    对R₁重复上面的过程, 就可以获得第二阶IMF分量。通过EMD方法对信号的一次次的筛分，就可以获得信号的多个IMF分量和一个逼近分量R_n，从而信号可由下式表示：

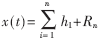
    因此，对任何一个信号x(t)，都可以将其分解为n个固有模态分量和1个残余分量R_n之和，其中，分量h₁，h₂，…h_n，包含了信号从高到低不同频率段的成分，且这些成分在频域相互正交，而R_n则表示了信号x(t)的整体趋势。
    以上分解过程可以解释为时空尺度滤波的过程，每一个IMF分量都反映了信号的不同特征尺度的分量，代表着信号的非线性非平稳信号的内在模态特征。若各阶IMF都满足Hilbert变换的前提条件，可以对它们作Hilbert变换：

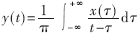
    x(t)和y(t)形成一复共轭对，则其解析信号z(t)=x(t)+iy(t)=a(t)e^iθ(t)，幅值函数a(t)=相位函数

    再对相位函数求导即得IMF分量的瞬时频率为：得到信号的Hilbert谱：更进一步，通过对时间积分可获得信号的Hilbert边际谱：

1.2 一维EMD的应用
    这里选取三个正弦函数(一个频率较低且幅值较大，另两个频率较高且幅值较小)和一个阶跃函数的叠加信号，对其进行四层EMD分解，如图1所示。图1中，从左到右是原始信号，从上到下是第一层到第四层IMF分量及四层分解后的残余。实验结果证明，信号经EMD后得到了从高频到低频不同频率段的成分、残余代表信号的主要趋势。如果两个相对高频的正弦函数成分为噪声，则得到的残余成分非常接近于能量较大的低频正弦函数成分和阶跃函数成分的叠加。如图1(f)所示的一个波形。实验结果很明显地反映了EMD的去噪" title="去噪">去噪作用，而且这种去噪是完全自适应性的处理，效果理想。从图中也可看出，一维EMD存在边界效应，现已有一些研究人员提出了解决办法，如Huang提出的用特征波CW对原始信号进行延拓的方法、基于神经网络技术对数据序列进行延拓的方法、基于AR模型的Levinson-Durbin算法的线性预测的方法以及采用最大熵谱(即Burg)估计进行边界延拓的方法，一定程度上避免了边界效应。

2 二维EMD的实现及应用
2.1 基于一维EMD提出二维EMD方法的实现
    (1)求曲面局部极值点就是求出曲面上所有的比周围临近点都大或都小的点。本文采用3×3（或5×5或7×7，总之是奇数维）数组，通过中心点与周围点比较分别确定极大值点和极小值点。对于一般边界数据的处理，因为只有在一半的邻域内有数据，所以只能在1/2的邻域区间内寻找极值点。对于四个角处的数据处理，则考虑1/4邻域区间。
    (2)极值点找出来之后，要对各极大值点和各极小值点分别进行曲面拟合。本文采用三角剖分结合线性插值" title="插值">插值或立方插值进行曲面拟合。三角剖分支持呈散射状分布的数据点的插值且速度较快。这样，经插值后得到极大值点曲面包络和极小值点曲面包络，将两曲面数据求平均得到均值包络曲面数据。
    (3)用原始曲面减去均值包络曲面。
    (4)与一维EMD方法相似需计算终止条件，这里用max_ima表示减匀前曲面数据的最大值的绝对值，用max_imd表示该曲面的均值包络曲面数据的最大值的绝对值，计算终止条件：，收敛速度较快些。
2.2 二维EMD的应用
    根据上述二维EMD的分解原理和分解方法，本文对标准Lena图像进行五层的EMD分解，其结果如图2所示。图2中，从左到右是原始信号，从上到下是第一层到第五层二维IMF分量，依次得到从低频到高频的不同频带范围内的分量。高频分量代表图像的细节，与现有的几种提取图像边缘的方法相比，这里提取的细节更为全面，同时又只携带了很少的能量。用EMD将图像分解成各层细节和轮廓（残余）之后也为图像进一步处理（如图像增强、图像压缩等）提供了新的前提。在将图像分解为高频、次高频等分量的过程中，图像中各点经历着提取自身的相对高频、次高频的过程，所以，相信基于这种方法的图像处理效果与以往的处理方法相比会有所不同，效果更自然，有其独特的视觉意义。

参考文献
[1] HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis.Proc.R.Soc.Lond.A454，1998：903-995.
[2] WU Zhaohua，HUANG N E.A study of the characteristics of white noise using the empirical mode decomposition method.Proc.Roy.Soc.London A，Dec，2002.
[3] 钟佑明，秦树人，汤宝平.Hilbert-Huang变换中的理论研究[J]．振动与冲击，2002，21(4)：13-17．