摘 要： 采用VHDL语言，在FPGA上实现了单精度" title="单精度">单精度浮点除法器" title="除法器">除法器的设计，通过采用SRT算法、SD表示法、常数比较法以及飞速转换法，进一步提高电路的运算速度" title="运算速度">运算速度。使用NC－sim和Maxplus2仿真软件进行前仿真和后仿真，使用Synplify进行逻辑综合，采用EPF10K40RC208-3芯片，对除法器进行了仿真。
    关键词： 除法器  SRT  单精度浮点  数字循环法  仿真

    在语音通信、图像处理等领域中，系统往往涉及大量的数据处理，而且数据计算精度和实时性要求很高，需要很高的浮点处理能力来提高系统的执行效率。Soerquist等人^[1]指出，在四种基本浮点运算中，浮点除法的执行速度最慢，处理器执行浮点加法和浮点乘法时，一般需要2～3个机械周期，而浮点除法则需要8到60个机械周期。然而，在浮点运算中浮点除法占的比例较小。Oberman和Flynn认为^[2]在所有浮点指令中，浮点加法指令占55%，浮点乘法大约占37%，浮点除法大约占3%，与浮点加法和浮点乘法相比，浮点除法的比例很小。但是，这并不表示浮点除法对处理器性能的影响很小，在因为浮点指令阻塞等待而引起的处理器性能下降的因素中，浮点除法指令大约占40%，浮点加法大约占42%，浮点乘法大约占18％。由此可见，浮点除法虽然出现的频率较低，但对处理器整体性能有较大的影响。因此设计一种执行效率较高的浮点除法结构对处理器性能的提高具有很重要的意义。
1 SRT算法的优点
    在处理单精度浮点数时，处理除法器的算法主要有两种：函数迭代法及数字循环法。由于函数迭代法所提供的商的最低位不准确，导致四舍五入操作无效，不能满足IEEE 754标准对精度的要求，而且它不产生余数，循环部分的执行复杂性程度较高。Oberman和Flynn的研究[2]表明数字循环算法可以取得较好的延时和面积平衡。数字循环算法是以加法和减法运算为基础的算法，需要多个循环周期，但是，该算法的实现比较简单，所需的硬件面积较小，功耗也较小，非常利于芯片的设计。
    该算法的实现主要有三种方法：恢复余数算法、不恢复余数算法以及SRT^[3](Sweeney，Robertson and Tocher)算法。传统的除法器采用恢复余数算法或不恢复余数算法，但是这两种算法的运算速度较低，每次循环仅能产生一位的商数字，需要较多的循环次数" title="循环次数">循环次数才能达到需要的指标。在每次循环时，恢复余数算法都需要将被除数或部分余数与除数进行比较，如果除数较大，还需要将部分余数恢复到上一次循环的数值。不恢复余数算法虽然不需要将部分余数恢复到原来的数值，但是商的数字集会出现负值，最后需要额外的加法器，将商的正数部分与负数部分相减。SRT算法是不恢复余数算法的扩展，具备了不恢复算法的优点，而且每次循环可产生log₂r位结果(r为基数），大大减少了循环的次数。基于SRT算法的优点，并考虑到本除法器应用在自动语音编码，本文所设计的除法器采用SRT算法进行除法运算。
    SRT算法由下面的表达式来确定商和余数：
   
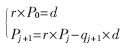
    d表示除数；P_j+1表示第j次循环后的部分余数；r表示SRT算法的基；q_j+1表示第j次循环得到的商，q_j+1的值由除数和部分余数组成的商数字选择函数决定。最后的商为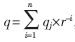，最后的余数为：。
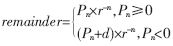2 单精度浮点除法器的设计
    本文是针对IEEE 754单精度浮点数据格式进行的浮点除法器设计。IEEE 754单精度浮点格式：A=(-1)^s×M×2^E-127，s表示符号位，E表示偏移码，E-127表示阶码，M表示尾数。
    除法器运算操作分四步进行：
    (1)确定结果的符号，对被除数和除数的符号位做异或操作。
    (2)计算阶码，两数相除，结果的阶码是被除数的阶码与除数的阶码的相减。
    (3)尾数相除，采用SRT算法进行尾数相除，被除数和除数的实际尾数都是24位数，即尾数实际为1.M，最高位1是隐藏位。
    (4)结果格式化，将结果整合为单精度浮点格式的标准。
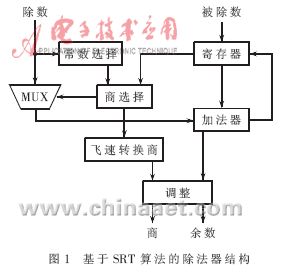
    在进行尾数部分处理时，虽然被除数和除数的实际尾数均为24位，但考虑到最后格式化以及商的数值的要求，实际上需要进行处理的位数为26位。因此，根据SRT算法公式，要使得循环次数减少，并且面积适中，必须选择适合的基数。而且每次循环时都需要与除数进行比较，若26位数进行比较，则延时较大，必须选择位数较少的数值代替26位的除数。为了适应自适应语音编码对速度的需求，本文针对上述两个需要进行时序改善的地方，设计了基4的SRT算法的除法器结构，如图1所示。

                           
2.1 基数的选择
    考虑到部分余数以及基数实现的简单性，本除法器选择SRT算法的基数为2的幂次方。基数大小和所需的循环次数成反比，基数越大，实现除法所需要的循环次数越少。但是基数增加，会导致商数字选择函数复杂性的提高，而且商数字选择函数往往处在关键路径上，其复杂度的增加无疑增加了每次循环的时间延迟。另外，大基数使得产生所有可能商的乘积的硬件电路变得复杂，增大了每个循环周期。因此，在实际应用中，SRT算法的基数一般限制在2或4。相比较而言，基4的性能较优，每次循环产生的位数为基2的两倍，Oberman的研究^[4]表明，基4除法的速度几乎是基2除法速度的2倍，而且更有利于进一步优化，降低整体的时间延迟。因此，在平衡面积和速度方面，本除法器的SRT算法选取基4，这样可以用较小的面积消耗换取较快的速度。
2.2 商数字集
    由于SRT算法的基数选择了4，因此，商的数字集不再是{0，1}，而是{0，…，3}。在传统的非冗余表示法中，商的每一位仅由一个正确的有效值表示，因此在确定每一位商数字时，需要将部分余数和除数进行完整的比较，即24位数的比较，效率较低。为了进一步提高除法器的运算速度，本除法器采用Avizienis^[5]介绍的冗余商数字集SD，它是一种对称的冗余表示法，商数字集表示为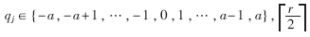≤a≤r-1，冗余因子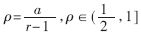。在确定每位商数字时，仅需要将部分余数和除数进行粗略的比较，不要求当前循环确定的商准确，可由下次循环修正，商的选择余地较大，而且产生的所有可能商的乘积数目较少，可以简化商数字选择函数。对于基4来说，商数字集只有两种选择，最小冗余{-2，-1，0，1，2}和最大" title="最大">最大冗余{-3，-2，-1，0，1，2，3}，Oberman的研究^[4]表明采用最大冗余商数字集的商数字选择函数速度比最小冗余的快20%,而且面积小50%，因此本除法器采用商数字集的最大冗余表示法。
2.3 商数字选择函数
    商数字选择函数的功能是从商数字集中有效地选择出正确的商数字，它是除法器的核心。由于商数字集选择了最大冗余，因此商数字选择公式如下：
    q_j+1=k∈{-3，-2，-1，0，1，2，3}
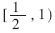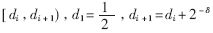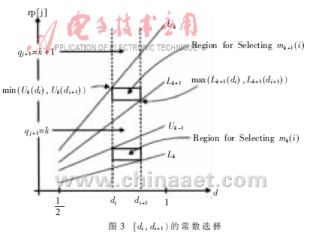
    如果d(k-1)≤rp[j]    由基4最大冗余的Robertson图^[6]可见(如图2所示)，部分余数的有效区域共分8个小区域，相邻区域有部分区域重叠，每个商数字都有两个区域与之对应，就是说允许商数字有两个选择，不正确的可通过下次循环进行纠正。但是，有效地判断部分余数所在的区域，选择比较接近的商数字，可以提高商数字选择函数的执行效率和实现的简单性，因此必须选取合适的区域分界点。传统的做法是通过PD曲线法来求得各区域的分界点，但是需要将部分余数和除数进行比较，24位数比较产生的时延较大，而且商数字选择函数的实现比较复杂。为了简化商数字选择函数，提高除法器的运算速度，本除法器采用常数选择法，用常数来代替除数进行比较，将所需要进行比较的位数缩小，降低这部分引起的时间延时，而且实现起来比较简单。其主体思想是把分解成若干个小区域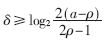，，然后判断除数的合适区域，再确定比较常数及每一位商数字所对应的区域，最后根据部分余数确定每一位商数字。常数选择法如图3^[7]所示。
     

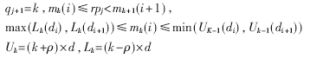
    根据最大冗余基4的商数字集，区域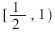可以分成两个小区域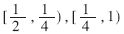，相应的比较常数集分别为{-3/2，-1，-1/2，1/2，1，3/2}和{-2，-1，-1/2，1/2，1，2}，这些比较常数就是每位商数字所对应区域的分界点。由所得到的两个比较常数集可知，在确定商数字时，仅需要比较部分余数的高三位，而不需要比较24位，产生的延时较小，而且硬件实现比较简单。
2.4 飞速转换
    SD表示的商数字集可以简化商数字选择函数的实现，但是商数字集会出现负值，最后需要一个加法器，将商的正数部分与负数部分相减。24位数的相减，位传递产生的时延比较大，而且由于商数字的选取空间比较大，会出现最后余数为负的现象，需要对其进行修正。同时，商也需要进行操作，效率较低。较好的转换方法是飞速转换法^[8]，它采用移位的方法来完成SD表示的商数字集的转换，而不采用相减的方法，这样就不存在借位的问题，效率较高，可以降低时间延时。其转换公式如下：
   
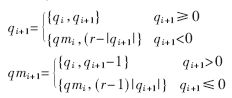
    当完成最后一次转换后，需要根据最后余数的符号来选择正确的商，如果最后余数为负，则商选择qm_i+1，否则商选择qi+1，则最后余数的选取不需要进行修正。
3 除法器的仿真实现
    根据所设计的结构，编写本单精度除法器的Verilog模型，在NC-sim进行前仿真，然后利用Synplify以Altera FLEX10K工艺库的EPF10K40RC208-3芯片的参数进行综合，最后完成的单精度除法器的规模为778个LUT，频率为20.8MHz。在Max+plus2进行后仿真，输入除数为424A8000(1.01×2¹²⁷)，被除数为3FA00000(1.10010101×2¹³²)，运算结果为42220000（1.010001×2¹³²），余数为2F000000(0)，时序图如图4所示，最后下载到芯片上运行。

                            
    本文给出了单精度浮点除法器的设计，结合当前比较流行的SRT算法与飞速转换法对除法器的关键部分进行时间延时的改善，具有高精度性及较宽的运算范围，可以满足自适应语音编码的要求。
参考文献
[1] SOERQUIST P，LEESER M.Area and performance tradeoffs in floating-point divide and square-root implementations.ACM Computing Surveys(CSUR)，1996，28(3)：518-564.
[2] OBERMAN S，FLYNN M J.Division algorithm and implementations.IEEE transactions on computers，1997，46(8)：833-854.
[3] HARRIS D L，OBERMAN S F，HOROWITZ M A.SRT division architectures and Implementations.Computer systems
laboratory stanford university，1997.
[4] OBERMAN S F.Design issues in high performance floating point arithmetic units.PHD thesis，stanford university，Electrical and electronic department，1997，1.
[5] AVIZIENIS A.Signed-Digit number representations for fast parallel arithmetic.IRE transactions on electronic computers，EC-10：389-400，1961，9.
[6] WILLIAMS T E，HOROWITZ M.SRT division diagrams and their usage in designing custom integrated circuits for division.Computer systems laboratory department of electrical engineering stanford university.1986，10.
[7] NIKMEHR H.Architectures for floating-point division.The university of adelaide australia.2005，8.
[8] JAMES E.S.Digital computer arithmetic datapath design using verilog HDL.Kluwer academic publishers.2004：108-112.