摘 要： 提出了一种可以应用于CDMA系统的多步长功率控制算法" title="控制算法">控制算法，本算法根据接收端的实测信干比" title="信干比">信干比与目标信干比的差值，从4个步长中选取一个，对发射端的发射功率" title="发射功率">发射功率进行调整。由于步长是有限个固定值，因此该算法易于实现。通过仿真证明，该算法性能优于可实际应用的FS算法，接近于性能理想而难于实现的FMA算法。
    关键词： 功率控制  多步长  FS算法  FMA算法  信干比

    CDMA系统是一种自干扰系统，其容量受限于系统的干扰水平。在CDMA系统中，必须在满足传输业务要求的信干比(SIR)条件下，尽量降低发射端的发射功率。因此在CDMA系统中功率控制技术具有非常重要的作用。有效的功率控制技术可以很好地控制远近效应和多址干扰，从而提高系统容量。在现有的功率控制算法中，Foschini和Miljanic提出的FMA算法^[5]是一种具有理想性能的经典算法。在FMA算法中，每次迭代后发射功率的改变幅度可以选取需要的任意值,而在实际系统中这是在一定技术条件和成本条件下难以实现的，因此FMA算法的意义仅仅停留在理论研究上。Kim在文献[7]中提出的定步长（FS）算法则是在每次功率更新中对接收SIR进行判决以确定对发射功率进行增加或减少,其步长固定，通常为1dB或0.5dB。FS算法在实际应用方面具有明显的优势，在第二代IS－95系统和第三代WCDMA系统中都采用了该算法。但由于FS算法在每次迭代中对发射功率的改变幅度是固定的，其收敛速度和收敛精度无法兼顾，因此该算法性能不够理想。
    针对FMA和FS算法的不足，本文提出了一种可以应用于实际系统的多步长（MS）功率控制算法，采用4个确定步长，在每次迭代中根据需要选取一个对发射功率进行调整。显然这是一种可以实际应用的算法。由于有大小不等的多个步长，因此在对发射功率进行调整的过程中可以获得较高的收敛速度和精度，其性能应优于FS算法。本文对MS算法和FS算法以及FMA算法进行了仿真，结果显示，本算法在性能上远远优于FS算法，与FMA算法的性能比较接近。
1 系统模型
    假设一个蜂窝小区中有N个移动台" title="移动台">移动台共用一个信道，并且假设移动台i属于第i个基站。本文中只考虑上行链路" title="链路">链路的情况。γ_i表示第i个基站接收到第i个移动台信号的CIR，当γ_i大于等于给定的目标信干比γ^tgt时，可以认为基站能够正确接收该移动台的信号。γⁱ可以用下式表示：
   

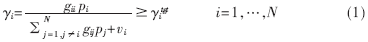
其中p_i表示移动台i的发送功率；g_ij表示移动台j到基站i的路径增益，该路径增益由路径衰落、阴影衰落和多径衰落共同组成；v_i是基站i处的背景噪声。所有的g_ij组成的矩阵称为链路增益矩阵，记为G。将G中元素归一化得到矩阵H,H中的元素h_ij=γ_i^tgtg_ij/g_ii，h_ii=0，η_i=γ_i^tgtv_i/g_ii。若考虑时变信道，则H矩阵中的元素值随时间的改变而改变，可用下式表示：

其中H^av表示H矩阵的均值，是一个确定值，而ΔH(k)在每次迭代中是一个按某个分布随机产生的不确定值。（2）式用元素形式表示如下：

其中p为发送功率矢量，H^{a v}为归一化的链路增益的均值矩阵，η为噪声矢量。本文中功率控制问题主要涉及通过测量γ_i的值并结合γ^tgt来确定发送功率矢量p，使得矢量p收敛于最佳发送功率矢量p^opt，即：

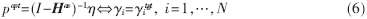
    由于实际系统中移动台有最大发射功率限制，用下式对发射功率进行限制：

其中p^max为移动台最大发射功率。假设（5）式在（7）式的范围内有解并且矩阵H(k)的谱半径小于1，则称系统是可行的。H矩阵的谱半径为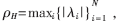其中λ_i是H矩阵的特征值。

2 功率控制算法
    将新功率控制算法表示如下：

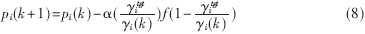
其中p_i(k)是第i个移动台的发射功率，γ_i(k)是基站在第k次迭代中接收到第i个移动台信号的CIR，f(·)是一个有上下边界的奇函数，本文采用sign(·)；α(·)是一个分段函数，表示每次迭代对功率值的改变幅度。在本文中不考虑时延的影响。由（8）式可知本功率控制算法是一个一阶完全分布式功率控制算法。如果取常数1并且取恒等函数，则本算法退化为文献[5]中的FMA算法；若取常数1且f(·)取符号函数，则算法退化为文献[7]中的FS算法；而在文献[8]中考虑了当α(·)取常数1时采用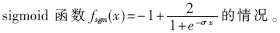

    考虑到实际系统有最大发射功率限制，将(8)式表示如下:

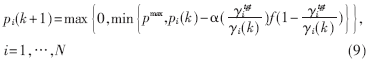
其中p^max是最大发射功率。在本算法中假设接收端可以得到γ_i^tgt和γ_i的值，（在上行链路中接收端是基站），而发送端可以得到p_i(k)的值。接收端通过对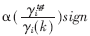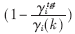进行计算，获得功率控制指令，然后将其反馈到发送端以更新发射功率。

    定义：对于H矩阵，如果满足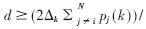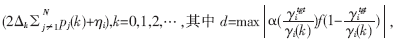则对γ_i的任意初始值γ_i(k=0)，γ_i(k)都将收敛于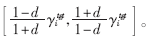证明参见文献[8]。

3 仿真分析
    在本文的仿真中考虑8个移动台共用一个信道的情况。用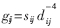表示平均链路增益，其中s_ij为阴影衰落因子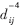，表示自由空间衰落，d_ij为基站i和移动台j之间的距离。仿真中小区半径设为1 000米，每个移动台与基站的距离在0～1 000米随机产生，每个移动台初始发射功率在0～1W随机产生，最大发射功率p_max=1.995 3W。阴影衰落服从对数正态分布，即s_ij=10^ζ/10，其中ζ是均值为0标准方差为8dB的高斯随机变量。目标信干比采用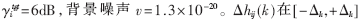范围内按照均匀分布随机取值。未扩频信号速率R=8kbps，扩频码片速率w＝1.28Mcps，对FMA、FS算法以及本文提出的MS算法进行仿真。将FS、FMA、MS分别用dB形式表示如下：

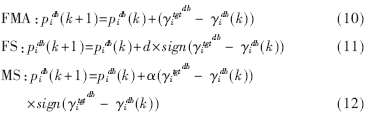
其中(11)式中的d取1，(12)式中的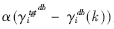为一分段函数，用于确定每次迭代的步长，表示如下：

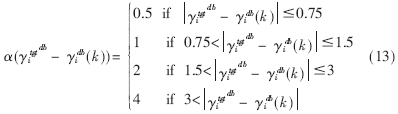
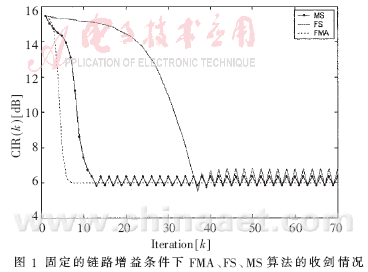
    首先在固定的链路增益（Δ_k=0）条件下分别运用三种算法进行仿真。仿真结果用图1表示。

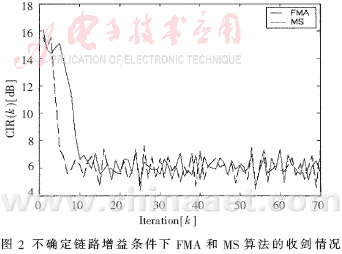
    由图1可以看出，与FS算法相比，MS算法具有更快的收敛速度和更好的收敛精度，其性能比较接近FMA算法。然后在不确定链路增益（Δ_k=0.2）条件下的分别运用以上三种算法进行迭代运算。仿真结果如图2和图3所示。其中图2显示了FMA和MS算法的结果，图3则是FS和MS的仿真结果。图2证明在时变信道中MS算法可以获得接近FMA算法的性能；而由图3可以看到，MS算法的性能明显优于FS算法。

    定义代价函数如下式：

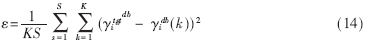
其中K表示调用功率控制算法的次数，S表示每次调用功率控制算法过程中进行迭代的次数。
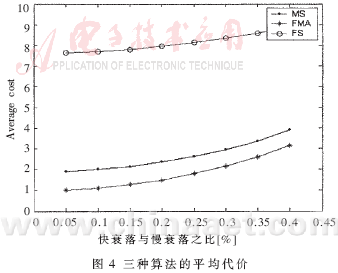
    代价函数实质上反映的是功率控制算法的收敛速度与精度的综合指标，通过代价函数计算得到的数据越小，算法的性能越好。仿真中S＝300，K＝1 000。仿真结果如图4所示。图4中的横坐标表示快衰落的最大值与慢衰落之比。通过图4可以得到这样的结论，最大快衰落与慢衰落之比在0.05～0.4的条件下，MS算法的代价都远远小于FS算法，略大于FMA。

    本文提出了一种多步长的功率控制算法，该算法是一种可以实际应用的算法。通过在慢衰落和快衰落环境中的仿真研究，证明该算法比FS算法具有更快的收敛速度和收敛精度，与理想的FMA算法比较接近。
参考文献
[1] AEIN J M. Power balancing in systems employing frequency reuse. COMSAT Tech.Rev., 1973,3(2).
[2]  MEYERHOFF H J.Method for computing the optimum power balance in multibeam satellite. COMSAT Tech.Rev.,1996,4(7):772-775.
[3]  ZANDER J. Performance of optimum transmitter power control in cellular radio systems. IEEE Trans.Veh,Technol.1992,41(1):57-62.
[4]  ZANDER J. Distributed cochannel interference control in cellular radio systems. IEEE Trans.Veh,Technol.1992,41(3):305-311.
[5]  FOSCHINI G J, MILJANIC Z. A simple distributed autonomous power control algorithm and its convergence.IEEE Trans, Veh, Technol.,1993,42(4):466-468.
[6] GRANDHI S A, ZANDER J, YATES R D. Constrained power control.Wireless Personal Commun.,1995,(4):257-270.
[7]  KIM D. On the convergence of the fixed-step power control algorithms with binarv feedback for mobile communication systems.IEEE Trans.Commun.,2001,49(2):249-252.
[8]  UYKAN Z, HEIKKI  N. Proportional power control algorithm for time varying link gains in cellular systems.IEEE Trans.Veh,Technol., 2006,55(1).