摘 要： 研究了基于混合核函数" title="核函数">核函数的最小二乘支持向量机（LS-SVM" title="LS-SVM">LS-SVM）的图像边缘检测" title="边缘检测">边缘检测技术，利用LS-SVM对图像像素邻域的灰度值进行了曲面拟合，通过混合核函数推导出了图像的梯度算子和零交叉算子，并结合梯度算子和零交叉算子实现了图像边缘定位。
    关键词： 边缘检测  最小二乘支持向量机  混合核函数  边缘检测性能

    边缘检测往往是其他图像处理技术的基础。传统的边缘检测算子如Sobel、Prewitt、Robert等，对噪声很敏感。近几十年来，有很多学者围绕边缘检测问题提出了很多算法^[1-4]。在边缘检测算法中，曲面拟合方法抗噪性强、检测精度高，是近年来出现的比较好的方法。近年来，支持向量机SVM(Support Vecror Machine)也得到了巨大的发展^[5]。其中最小二乘支持向量机LS-SVM[6](Least Squares SVM)在函数估计中应用较多。LS-SVM的许多特性是由所选择的核函数决定的，一种改进的方法是把多个核函数线性组合起来形成一种混合核函数[7]，由这种混合核函数构造的LS-SVM不仅学习能力强，而且具有很好的推广性。本文利用混合核函数（采用3×3大小的卷积核）对图像边缘提取进行研究。实验结果表明，在信噪比" title="信噪比">信噪比较小的情况下，该方法比单独使用高斯" title="高斯">高斯核或者多项式核进行边缘提取的性能要好。
1 LS-SVM
1.1 LS-SVM原理
    LS-SVM是统计学习理论中常用的方法，其思想如下：给定训练样本集，通过非线性变换φ(·)把n维输入向量x_i和输出样本向量y_i从原空间R_n映射到高维特征空间F，在此空间中构成最优线性决策函数：
       

式中，ω为超平面权值向量，b为偏置项。
    对于LS-SVM，可以得到如下线形方程^[8]：
     

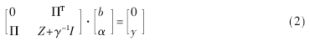
式中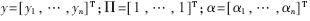，，表示拉格朗日乘子；Z_kn=φ(x_k)^T·φ(x_n)；常数γ>0，它对超出误差的样本的惩罚程度进行控制；I表示单位矩阵。
    根据Mercer条件，存在一个映射函数φ，并可选择一个核函数K满足下列条件：
   

    这样，基于LS-SVM的函数估计表达式为：
      

式中，α_k和b是(4)式的解，具体的形式取决于核函数K(x，x_k)的类型。
1.2 LS-SVM核函数分类
    目前研究最多的核函数主要有以下几类：
    (1)局部性核函数，仅仅在测试点附近的小邻域对数据点有影响。其中应用较多的是径向积核函数（RBF）：K(x，x_k)=exp{-|x-xk|²/δ²}，式中δ²是高斯核宽度。
    (2)全局性核函数，允许远离测试输入的数据点对核函数的值也有影响。其中应用较多的是多项式核函数（Poly）：K(x，x_k)=(x·x_k+1)d，式中d是多项式的次数。
    (3)混合核函数，因为局部性核函数学习能力强、泛化性能较弱，而全局性核函数泛化性能强、学习能力较弱，因此把这两类核函数混合起来^[9]。本文采用的K_mix=λK_poly+(1-λ)K_rbf就是混合核函数中的一种，并且满足Mercer条件。式中混合系数λ∈(0，1)。
2 基于LS-SVM的图像边缘检测
2.1 利用LS-SVM进行图像拟合的原理^[8]
    一幅二维灰度图像可以认为是一个连续的函数：y=f(x)：R²→R¹，x是二维向量，表示像素点的行、列坐标，输出y是一个标量，表示输入向量x所对应的像素点的灰度值。通过LS-SVM算法可以在像素邻域大小确定的情况下构建出输出向量和像素点之间的关系。令Ω＝Z+γ^-1I，A=Ω^-1，B=Π^TΩ^-1/Ω^TΠ^-1Π，则由式（2）可以得到如下等式：
       

式中，A和B在实际计算中可以预先计算，与图像灰度值无关，从而降低了实时运算的复杂度。通过选用不同的核函数可以得到不同的曲面拟合形式。
    设R和C为原始图像中某一个像素的对称邻域内的坐标集，例如R={-1，0，1}，C={-1，0，1}。在混合核函数的LS-SVM中，定义在矢量空间的图像灰度曲面拟合函数可写成如下形式：
   

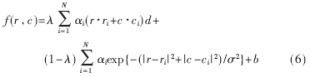
式中，α_i、b是（2）式的解，d是多项式的阶次， ?姿是混合系数，?滓2是高斯核参数，f(r，c)是点(r，c)的灰度估计值。
2.2 图像梯度算子和零交叉算子计算
    采用混合核函数的LS-SVM进行图像曲面拟合时，对于点(r，c)，其一阶和二阶的水平和垂直方向上的偏导数如下：
    

式中，E=exp{-(|r-r_i|²+|c-ci|²)/δ²}，D=(r·r_i+c·c_i)。根据式（5）把?琢的关系式带入偏微分方程（7）～（10）式中，可得：
   

    可以看出，图像的梯度算子和零交叉算子可以由支持向量机核参数和卷积核大小直接求出，不用训练，实现起来比较容易，而且梯度算子和零交叉算子是来自于同一LS-SVM拟合曲面函数，因此可以同时综合梯度和零交叉点进行边缘的定位和检测。
2.3 图像边缘检测算法的实现
    (1)采用高斯滤波器对图像进行去噪预处理；
    (2)利用模板F_r、F_c和图像卷积得到图像水平、垂直方向的梯度，并对梯度进行阈值化，得到梯度所确定的边缘图S1；
    (3)利用模板F_u和图像卷积得到图像二阶导数并查找零交叉点，得到基于零交叉点的边缘图S2；
    (4)对边缘图S1和S2进行“与”运算，得到边缘图S；
    (5)去除边缘图S的离散点，并对其细化，得到最终的边缘检测图。
3 实验分析
3.1 边缘检测的性能指标
    Abdou和Pratt提出了一种评价边缘检测性能的客观标准^[10]，其定义为：
     

式中，I_i表示实际检测到的边缘像素点与最近的理想边缘像素点之间的距离；ID和IL分别为实际检测到的边缘像素个数和理想的边缘检测像素个数。α是惩罚因子，取0到1之间的正数。实验中采用图1所示的测试图像，通过对测试图像引入噪声，利用不同的核函数算法对噪声图像进行边缘提取，得出边缘检测性能指标P， P值越大，说明检测的性能越好。
                       

3.2 实验结果分析
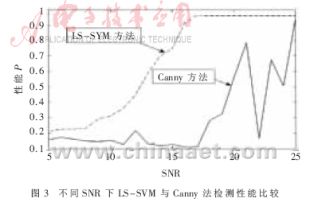
    利用混合核函数的LS-SVM算法提取图像边缘，混合系数与边缘检测的性能紧密联系。在SNR=10dB时比较了大小为3×3的卷积核对应不同的混合系数所得到的性能，并在不同信噪比情况下同Canny法进行比较，其结果如图2和图3所示。
                             

    在图2中，λ＝0时对应的是径向积核函数LS-SVM的边缘检测性能；λ＝1时对应的是多项式核函数LS-SVM的边缘检测性能；当λ取0到1之间的数值时对应的是混合核函数LS-SVM的边缘检测性能。从图2可以看到，若能选取适当的混合系数，采用混合核函数的LS-SVM所得到的边缘检测性能要优于单独使用多项式核函数或者径向积核函数的LS-SVM算法所得到的边缘检测性能。图3则表明在噪声情况下混合核函数的LS-SVM算法的检测性能要优于Canny方法的检测性能。利用LS-SVM方法和Canny法分别提取Lena,Rice图像的边缘效果图如图4所示。

                              
    实验中采用图1所示的合成测试图，分别加入信噪比为5dB、10dB、15dB、20dB、25dB的高斯噪声进行边缘提取，几种边缘检测性能P的值如表1所示。

                       
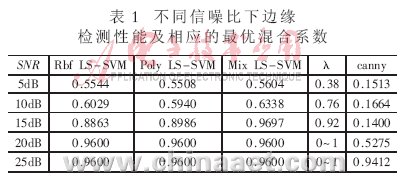
    从表1可以看出，利用LS-SVM方法比Canny方法可以获得更好的边缘检测性能。而利用LS-SVM提取图像边缘时，在信噪比较高的情况下采用混合核函数得到的性能和单独使用高斯核函数或者多项式核函数的性能是一样的，但是在低信噪比的情况下，通过采用不同的混合系数，混合核函数所表现出来的性能要比单独使用高斯核或者多项式核函数的性能更好。
    本文利用最小二乘支持向量机对图像像素邻域的灰度值进行曲面拟合，在核函数为高斯、多项式以及混合核时，直接求出图像灰度拟合曲面的一阶和二阶导数，从而得到梯度算子和零交叉算子。为进一步反映该算法边缘检测性能，本文通过实验确定了不同信噪比下的最佳混合系数，通过与Canny法比较得到了如下结论：
   (1)基于LS-SVM的边缘检测方法在有噪声情况下可以获得比Canny方法更优越的性能；
   (2)在信噪比较高的情况下，采用混合核与采用高斯和多项式核的LS-SVM获得的性能是一样的，此时混合系数的大小与检测性能无关；
   (3)在信噪比较低的情况下，通过选择合适的混合系数，采用混合核的LS-SVM获得的检测性能要优于采用高斯核、多项式核的LS-SVM获得的检测性能。
参考文献
[1] CANNY J.A computational approach to edge dection[J].IEEE Tran on Pattern Analysis and Machine Intelligence，1986，6(6)：679-698.
[2] RISHI R R，CHAUDHURI P.Thresholding in edge detection：a statiscal approach[J].IEEE Tran on Image 
Processing，2004，13(7)：927-936.
[3] 修保新.图像模糊信息粒的适应性度量及其在边缘检测中的应用[J].电子学报，2004，32(2)：274－277.
[4] VANDEWEIJER J，GEVERS T.Edge and corner detection by photometric quasi-invariants[J].IEEE Tran on Pattern Analysis and Machine Intelligence，2005，27(4)：625-630.
[5] VAPNIK V.An overview of statistical learning theory[J].IEEE Trans on Neural Networks，1999，10(5)：988-999.
[6] SUYKENS J A K，VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters，1999，9(3)：293-300.
[7] SMITS G F，JORDAAN E M.Improved SVMRegression using Mixtures of Kernels[C].Proceedings of the 2002 
International Joint Conference on Neural Networks.Hawaii：IEEE，2002.2785-2790.
[8] 刘涵，郭勇.基于最小二乘支持向量机的图像边缘检测研究[J].电子学报，2006，7(7)：1275－1279.
[9] Sheng H.An SVM-based Small Target Segmentationand Clustering Approach[C].Proceedings of the Third 
International Conference on Machine Learning and Cybernetics.Shanghai：IEEE，2004：3318-3323.
[10] ABDOU I E，PRATT W K.Quantitative design and evaluation of enhancement thresholding edge detectors[J].
Proc IEEE，1979，67(5)：753-763.