摘 要： 通过对滚动轴承振动信号的分析处理，提出了基于独立分量分析" title="独立分量分析">独立分量分析和支持向量机" title="支持向量机">支持向量机的故障诊断" title="故障诊断">故障诊断方法，采用FastICA算法对信号进行分析处理，提取出代表轴承运行状态的投影系数矩阵，并以此作为特征向量来建立支持向量机分类器，利用SVM网络的智能性来判断滚动轴承的工作状态和故障类型。
    关键词： 独立分量分析  支持向量机  故障诊断  滚动轴承

    轴承作为重要的机械部件，在机械装置上被广泛应用。通过一种有效的故障诊断方法对轴承进行检测是必不可少的。对轴承故障的诊断过程实质上就是一个模式识别过程，其关键在于故障特征参数的提取和故障状态的识别。独立分量分析ICA（Independent Component Analysis）方法可以在无正交的条件下抽取信号的统计独立分量，在非高斯数据分析方面具有独特优势，采用ICA方法可以获取多维振动观测中有效的高阶统计特征。
    基于人工神经网络分类器的模式识别方法以其较强的自组织、自学习能力和非线性模式分类性能在机械故障诊断中得到了广泛应用。但人工神经网络存在一些诸如收敛速度慢、局部极小点、过学习等不足，且应用于智能故障诊断时需要大量的故障数据，这在实际中有时难以满足。支持向量机SVM(Support Vector Machines)采用结构风险最小化原理，较好地解决了过学习和欠学习问题，在解决小样本数据集及非线性问题上有独特的优势，具有比神经网络更强的泛化能力。
    本文提出了基于ICA和SVM的轴承故障诊断方法。首先对轴承振动信号用负熵快速ICA算法进行分析处理，选取用ICA方法得出的投影系数矩阵作为轴承所处的工况特征，然后把投影系数的行向量作为特征参数输入SVM建立SVM故障分类网络，进一步通过 SVM网络的输出结果来判断滚动轴承的状态和故障类型。仿真结果表明该诊断方法能有效实现轴承状态的识别。
1 支持向量机原理
    设训练样本输入为x_i, i=1,…,l,对应的期望输出y_i∈{+1,-1},其中＋1和-1分别代表两类的类别标识。假定分类面方程为w·x+b=0,为使分类面对所有样本正确分类并且具备分类间隔，则要求它满足如下约束：
   
    可以计算出分类间隔为2/‖w‖，满足式(1)并且使2/‖w‖²最大的分类面叫作最优分类面。Vapnik给出了最优分类函数，即决策函数是：
   
其中α_i为目标函数在约束条件,l下的极大值点，解中将只有一部分α_i不为零，其对应的样本就是支持向量（Support Vectors）。
    对于非线性问题，可以通过非线性变换将其转化为某个高维空间中的线性问题，在高维空间求最优分类面，只需选择适当的核函数" title="核函数">核函数K(xi,xj)就可以实现某一非线性变换后的线性分类，此时的决策函数为：
   

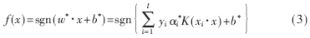
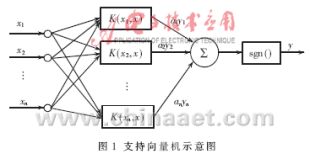
    目前常用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数等。支持向量机求得的决策函数形式上类似于一个神经网络，如图1所示，其输出是若干中间层节点的线性组合，而每一个中间层节点对应于输入样本与支持向量机的内积，因此也被称作是支持向量网络。

                           
2 ICA算法的原理
2.1 ICA问题描述
    ICA问题可简单描述为:设有m个未知的源信号s_i(i=1,2,…,m)的线性混合，构成一个列向量S=[s₁,s₂，…，s_m]^T。混合矩阵A是一个l×m矩阵，X=[x₁,x₂,…,x_l]^T观测信号矢量，且：X=A·S。ICA的任务是找到分离矩阵W，使得y=W·X,y=[y₁,y₂,…,y_m]就是从混合信号中分离出的独立源信号s的估计值。本文采用基于负熵的快速ICA算法——FastICA来实现独立原信号的分离。
2.2 FastICA算法
    本文ICA的训练算法采用基于负熵判据的FastICA，FastICA算法由观测信号的预处理和独立分量提取两部分组成，有关负熵判据FastICA的具体实现过程见参考文献[2]。下面是FastICA算法分离过程包含的几个主要步骤：
    (1)对观测信号x去除均值并白化处理得到具有单位方差的信号矢量;
    (2)随机选择具有单位方差的初始分离矩阵W;
    (3)计算;
    (4)对分离矩阵进行修正W=;  
    (5)如果分离矩阵收敛，则迭代逼近过程结束，否则返回(3)。
    得到分离矩阵W后，可以很容易求出源信号的估计为，若源信号中包含多个独立分量，可以重复上述过程进行分离。
2.3 用FastICA算法对轴承信号的仿真
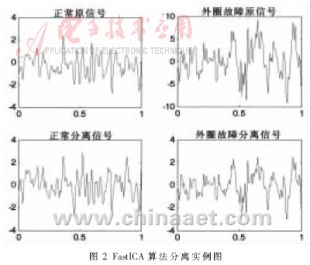
    对轴承的正常和外圈" title="外圈">外圈故障信号进行Matlab仿真，如图2所示分别为正常和外圈故障信号，然后采用二维的随机矩阵将正常和外圈故障信号进行混合，将混合后的信号进行Matlab仿真可以得到经过FastICA算法分离的波形。从波形上可以看出分离后的信号与原信号相比只是在幅值上发生了一些变化，信号波形的变化规律与原信号基本一致，所以分离后的信号可以很好地反映原信号的特征。

                           
3 基于ICA和SVM的滚动轴承故障诊断方法
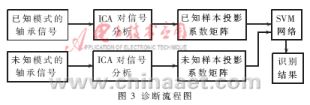
    基于ICA和SVM的滚动轴承故障诊断方法的流程如图3所示。首先用ICA对故障样本进行分析可以得到投影系数矩阵，利用此矩阵的行向量作为训练样本来训练支持向量机网络，最后将要识别运行状态类型的训练样本投影系数矩阵输入到训练好的SVM网络，就可以实现故障的模式识别。

                              
    其具体的方法如下：
    (1)分别在轴承正常、内圈故障、外圈故障和滚珠故障四种状态下，从历史数据中选取故障样本，然后将故障样本经过FastICA分析得到各种工况下投影系数。下面以提取外圈故障投影系数为例作具体说明：从历史数据中选取外圈故障时的数据X_F∈R^p×n(p为传感器数，n为采样点数），预处理后对其进行FastICA分析，即有X_F=A_F·S_n（S_n∈R^m×n，A_F∈R^p×m），经过变化可得：A_F=X_F·S_n⁺，S_n⁺表示矩阵Sn的广义逆，A_F为经独立分量分析计算出的投影系数矩阵。其他三种状态的投影系数矩阵可以同样得出来。
    (2)将四种工况下的投影系数矩阵作为训练样本输入支持向量机来建立SVM网络，如图4所示。支持向量机是两类分类器，要对滚动轴承多种状态类型进行分类是多类分类问题，可以将多类问题分解为多个两类问题，然后用SVM网络进行训练进而来识别状态类型。本文要识别轴承的正常、内圈故障、外圈故障和滚珠故障四种状态，针对这四种状态建立四个两类分类器(SVM0～SVM3)。用SVM0识别正常状态，SVM1识别内圈故障， SVM2识别外圈故障，SVM3识别滚珠故障。在识别过程中，只要上一个SVM分类器输出为－1，就会自动将特征向量输入到下一个分类器中，依此类推，直到SVM3。

                        
    (3)将测量的轴承信号通过FastICA的方法提取轴承投影系数矩阵，然后输入到经过训练的SVM分类器中，就可以实现故障的模式识别了。
4 仿真实例
4.1 网络的训练
    实验中要用到SVM_x(x=0,1,2,3)网络，网络的核函数选取径向基核函数。径向基函数的中心位置以及中心数目、网络的权值在训练的过程中自动确定。从历史数据中分别选取轴承的正常、内圈故障、外圈故障和滚珠故障四种状态的样本，每一个状态选取128个样本，用FastICA方法进行分析得到投影系数矩阵A_F，用AF去训练4个支持向量机，每一个支持向量机对应一个特定的故障，这样就得到了训练好的支持向量机网络。
4.2 故障的识别
    轴承状态的识别就是用训练好的SVM网络对轴承状态的分类：在轴承四种状态的历史数据中各随机选取32个样本作为测试信号。对测试信号进行FastICA方法的分析与处理后可以得到投影系数矩阵A_F′，然后将每一种状态的投影系数矩阵A_F′作为支持向量机的输入，进而识别轴承的状态，故障诊断的结果如表1所示，通过表1可以得出支持向量机具有较强的识别能力。为了进一步研究SVM在小样本下的识别能力，将训练样本减少到64个进行训练，然后对相同的32个样本进行状态识别，得到的结果如表2所示。通过比较表1和表2可以得出，支持向量机在训练样本减少的情况下，仍能对轴承的运行状态做出正确的判断，具有良好的泛化能力，也验证了基于ICA和SVM故障诊断方法的可行性。

                       
    通过对轴承振动信号进行FastICA算法处理，提取各种状态下的投影系数矩阵作为支持向量机网络的训练样本，用训练后的网络来实现轴承运行状态的智能识别，仿真实验结果表明利用ICA和SVM的诊断方法可以实现滚动轴承故障模式的识别，由于支持向量机适合小样本的诊断且拥有较好的泛化能力，此方法在故障数据有限的情况下仍可以有效诊断出轴承的工作状态和故障类型，为轴承的诊断提供了一种新的方法。
参考文献
[1] 肖健华.智能模式识别方法[M].广州:华南理工大学出版社，2006.
[2] 孟继成,杨万麟.独立分量分析在模式识别中的应用[J].计算机应用,2004,24(8):27-31.
[3] 邵华平,覃征，游诚曦.SVM算法及其应用研究[J]. 兰州交通大学学报(自然科学版)，2006,25(1):104-106.
[4] 焦卫东，杨世锡，吴昭同.机械故障模式识别的ICA基神经网络方法[J].计算技术与自动化，2003,22(2):63-67.
[5] 胡寿松,王源.基于支持向量机的非线性系统故障诊断[J]. 控制与决策,2001,16(5):617-620.
[6] 胥永刚，李强，王正英，等.基于独立分量分析的机械故障信息提取[J].天津大学学报,2006,39(9):1066-1071.