摘 要： 在分析其控制原理的基础上，提出了用整流器输入前端电压滞后角作为输入变量控制网侧输入电流" title="输入电流">输入电流的相位幅值控制的新方法，解决了传统相幅控制方法存在的问题。建立了基于三相静止坐标系和两相旋转坐标系的整流器数学模型" title="数学模型">数学模型，并验证了这个新的控制方法的有效性。
    关键词： 相幅控制  电压滞后角  调制度  坐标变换

    电压型" title="电压型">电压型PWM整流器以其日渐成熟的控制技术，广泛地应用于静止无功补偿、有源电力滤波、超导储能、电气传动等领域。近年来其控制技术在“间接电流控制”和“直接电流控制”两大方向上有了深入的发展。直接电流控制策略以快速的电流响应和鲁棒性倍受关注，针对固定输入已研究出各种不同的控制方案。当交流输入电压" title="输入电压">输入电压按一定规律发生变化时，电路参数的变化等因素直接影响控制方案的实施。本文在传统的相幅电流控制基础上，针对其网侧电流的动态响应慢、对系统参数变化灵敏等问题，提出改进的相位幅值控制方法，用整流器输入前端电压滞后角作为输入变量，控制网侧输入电流。通过模拟和仿真实验，验证了该控制方法的有效性，很好地解决了传统相幅控制存在的问题。
1 三相电压型PWM整流器建模
1．1 基于三相静止坐标系的数学模型
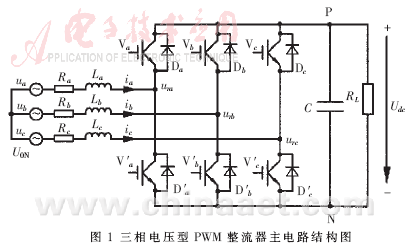
    三相电压型PWM整流器拓朴结构如图1所示，假设网侧输入电压为三相对称正弦波电压，输入电感线性不饱和，网侧输入电源中点电压为U_0N，令L_a=L_b=L_c=L_e，R_a=R_b=R_c=R_e，考虑纯电阻性负载，以电感电流为状态变量，对于基波分量，则有：

    以直流侧电容假想中点为参考地，由式（1）和（2）可导出网侧输入电源中点电压U_0N：

    利用单极性二值逻辑开关函数S_j(j=a、b、c)描述^[1]，即:

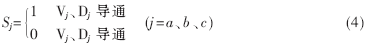
    根据主电路结构形式以及直流侧电压和整流器网侧输入电压之间的关系可得到三相电源中心点电压值U_0N为：

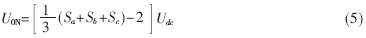
    将电路中P、N两点输出电压" title="输出电压">输出电压取为状态变量，有:

    综合式（1）、（5）和（6），可得到三相静止abc坐标系下电压型PWM整流器数学模型^[2]：

    式（7）为三相电压型PWM整流器的一般数学模型，具有物理意义清晰、直观等特点，但整流器交流侧均为时变交流量，不利于控制系统设计。因此，需通过坐标变换将三相静止abc坐标系变成以输入交流电压基频同步旋转的dq坐标系，将前者中正弦量转化成后者中的直流量，以达到简化控制系统设计的目的。
1．2 基于两相旋转坐标系的数学模型
    通过坐标变换，将三相静止abc坐标系变换成两相旋转dq坐标系，其中d 轴与三相电压合成矢量方向重合且以输入电压角频率ω 逆时针同步旋转，q轴超前d 轴90°。遵循等量变换的原则，可用如下变换矩阵描述：

    从而得到三相 PWM整流器在两相旋转dq坐标系下的数学模型:

式中，S_d、S_q为两相旋转dq坐标系开关函数。通过坐标变换，三相电压型PWM整流器数学模型得到简化。
2 PWM整流器相位幅值控制
2．1 传统PWM整流器相位幅值控制分析
    整流器拓朴如图1所示，对于单位功率因数电压型三相PWM整流器，假设输出电容的中点与交流输入电压中点等电位，整流器输入侧对此中点的电压波形与开关元件的触发波形一致 ,通过改变开关元件触发信号的相位及调制比就可以调整u_ra基波分量的相位和幅值。忽略电感电阻，其单相等效电路如图2所示，图3为对应功率因数λ为1和-1时的向量图。为输入电源电压、为桥臂中点电压即整流器前端电压的基波分量, 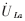为升压电感两端电压，为输入电流基波分量,δ为u_ra（基波分量）滞后于u_a的电角度。

    参见图2，在传统的相幅控制算法中,

    对于基波分量,

    当调制度为M时，PWM整流器前端输入电压基波分量为^[3]:

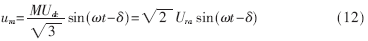
    传统的相位幅值控制，其控制方式是把直流侧输出电压的给定值与实际输出电压的反馈值的误差信号，作为相电流控制信号或者作为电感L_a两端电压控制信号。通过调整PWM的调制度M和控制角δ，控制电感L_a上电压的相位，可以使输入电流基波分量的相位与电源电压同相位或反相位。

    U_ra和δ通常由下式计算：

2．2 改进的PWM整流器相位幅值控制原理
    当角频率ω或幅值发生变化时，式(14)运算量较大，存在系统受电路参数影响大、不易实现实时控制等缺点。
    当δ在小范围内变化时，可将式(14)近似简化为：

    根据式（13）和（15），直接控制δ角就可以调节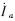与 的相位关系。

    采用直流侧输出电压的闭环控制方式，由PI调节器直接给出δ值，通过限幅器将δ值限定在（-π/4<δ<π/4）内，从而可大大减少计算量，易于实现实时控制。
    系统闭环控制结构图如图4所示^[4]，输出直流电压的给定参考值与实际反馈值的误差经PI调节器调节后作为δ值控制PWM脉冲生成器。δ值可用下式计算：

式中, β为电压反馈系数，k_PI为调节器传递系数。
    在PWM整流器控制过程中，调制度是一个重要的控制因素。根据式（12）可得：

    根据功率控制关系和图3可推导出调制度M与δ的关系：

    式(20)说明整流器的带载能力与电感L_a及调制度M有关。
    系统的调节过程：负载增大(R_L减小)时，整流器输入电流增加，U_dc减小，误差(U_ref-βU_dc)增大，控制角δ增大，电流I_a增大，电容C充电，电压U_dc回升，系统进入新的平衡工作点；相反，负载减小(R_L增大)时，也有类似的调节过程。
    综合上述分析，采用改进的相位幅值控制方法，根据调制度M与δ的关系，不论交流输入电压角频率ω或幅值如何变化，都可以通过PI控制器直接调节直流输出电压的给定值与实际输出电压反馈值的误差，给出δ值，实时产生PWM脉冲控制整流器，达到控制输入电流及功率因数的目的。
3 实验结果
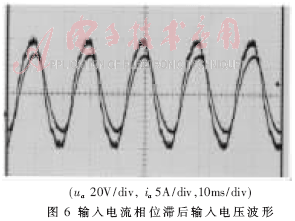
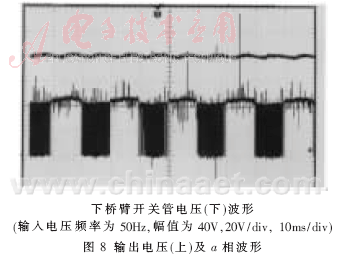
    对于上述改进的相位幅值控制方法，采用数字与模拟混合控制电路，进行了模拟实验。PI控制器由电压外环、电流内环构成，功率单元采用三菱PM15CSJ060型IPM。系统参数：输入电感L_e=8.5mH，直流侧电容C=1000μF，网侧输入电压(有效值)为10～70V，电源频率f=20～50Hz。实测实验波形如图5～图９所示，图５为输入电流相位超前输入电压波形；图６为输入电流相位滞后输入电压波形；图７为输入电压频率为50Hz，幅值为20V时输出电压(上)及a相波形；图８为输入电压频率为50Hz，幅值为40V时输出电压(上)及a相波形；图９为输入电压频率为25Hz，幅值为20V时输出电压(上)及a相波形。从实测波形中可以看出，输入电源电压频率和幅值变化不影响系统的稳定性。

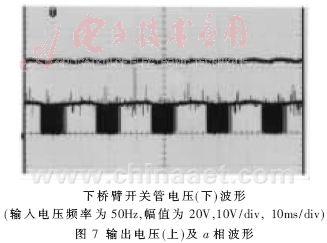
    通过调制度M和控制角δ的控制，可以任意调整输入电流与网侧输入电压之间的相位关系，达到调节功率因数的目的。该系统的稳定性高，控制算法简单，易于实现数字化控制。
参考文献
[1] 张崇巍，张兴.PWM整流器及其控制. 北京:机械工业出版社,2005.
[2]  徐德鸿.电力电子系统建模及控制.北京:机械工业出版社,2006.
[3]  陈国呈. 新型电力电子变换技术. 北京:中国电力出版社,2005.
[4]  JOSE R R，JUAN W D，JOSE R E，et al. PWM regenerative rectifiers：State of the Art. IEEE Trans.On Industrial Electronics,2005，52(1).