基于改进粒子滤波算法的人体运动跟踪
2008-07-17
作者：杨 柳，张宝亮，赵 建，张瑞
摘 要： 在复杂环境中对人体进行有效性和鲁棒性的跟踪是计算机视觉" title="计算机视觉">计算机视觉领域一个非常富有挑战性的课题，提出了一种基于改进粒子滤波算法" title="滤波算法">滤波算法实现的人体运动跟踪。利用改进的粒子滤波算法跟踪视频序列" title="视频序列">视频序列中的人体运动，不但解决了传统粒子滤波算法计算量大、误码多的缺点，而且能较好地处理遮挡和自遮挡问题。实验结果表明，该改进算法能更准确、更有效地跟踪运动人体。
关键词： 粒子滤波 人体运动跟踪 重采样
视频人体运动跟踪是计算机视觉领域中一项非常有挑战性的任务，近年来倍受关注。视频人体运动跟踪技术可广泛应用于体育运动分析、虚拟现实、计算机动画、视频监控、人机交互等领域。早期人体运动跟踪多采用Kalma滤波[1]这一传统技术。但是Kalma滤波要求目标状态必须满足高斯分布" title="高斯分布">高斯分布，对于复杂背景或有遮挡等造成的非高斯分布和非线性问题，往往会导致组合爆炸，且计算复杂度惊人，极易发生跟踪失败。而粒子滤波[2-3]方法对目标状态的分布没有任何要求，能很好地处理非线性和非高斯问题。自Bruno将粒子滤波引入到图像序列的目标跟踪中以来[4]，粒子滤波已成为视觉跟踪、机器学习和机器人定位等领域研究的热点。
目前，国内外对基于粒子滤波的人体运动跟踪的研究相对较少。本文介绍基于改进粒子滤波算法跟踪人体运动，不但解决了传统粒子滤波算法搜索时间长、容易漂移的缺点，而且比传统算法计算量小、跟踪精度高、稳健性强。
1 粒子滤波改进算法
1.1 粒子滤波算法
粒子滤波算法的核心思想是：为了求解数学或物理等方面的问题，首先建立一个概率模型或者随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察或采样试验计算所求参数的统计特征；最后给出所求解的近似值。
下面详细介绍粒子滤波的基本思想。
粒子滤波就是用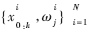
完全描述后验概率密度分布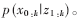
这里，x0：k={xj，j=0，…，k}，z0：k={zj，j=0，…，k}，分别表示各个时刻的系统状态和观测状态，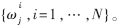
表示j时刻所对应的粒子
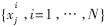的归一化权值" title="权值">权值，即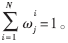
直接从后验概率p(x0：k|z1：k)中进行取样是比较困难的。假设存在π(x)，有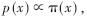
并且可以很方便地从π(x)中进行取样，这样的π(x)称作重要性密度。根据贝叶斯理论有：
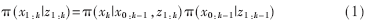
这样，就能很容易对系统状态进行估计，权值的递推方程可以写成：
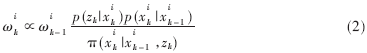
在k时刻的后验概率密度可以近似地写成：
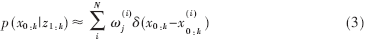
1.2 粒子滤波算法改进策略
传统的粒子滤波算法需要使用状态转移后的所有粒子进行系统观测和重采样。这使得计算量很大，而且增加了错误信息，甚至会导致跟踪目标漂移。鉴于此，笔者对传统的粒子滤波进行了一系列的改进。在对系统观测过程进行改进时，只选取局部最优粒子（即权值较大的粒子）进行状态转移；在重采样环节，也使用了这种局部最优原理，只选取部分大权值粒子。改进的粒子滤波算法,能够在很大程度上解决上述问题。
图1描述的是状态转移环节，当前时刻所有粒子对应的位置服从均匀分布。图中“○”表示跟踪目标在该时刻的真实位置，黑点表示该时刻的粒子，黑点的大小代表粒子权值的大小。
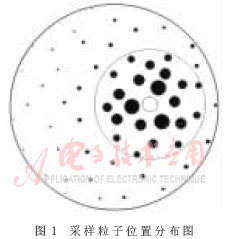
由图发现，离“○”越近的粒子权值越大，超出1/2粒子传播半径的粒子，权值可忽略。根据这种先验知识，基于局部最优化原理选取部分粒子。当利用粒子进行系统观测时，将粒子按权值大小依次排序，只需选取半数大权值粒子，就能很准确地计算出最优估计的位置。这种改进策略可使该环节的计算量减少40%。由于忽略了远处的粒子，剔除了部分错误信息，因此跟踪精度也得到了提高。
粒子重采样环节的改进是分裂粒子时只选取上述的半数大权值粒子。改进的重采样具体实现过程如下：将系统观测过程中使用的粒子，按大小排序均分为两组。权值大的一组，每个粒子分裂为三个新的粒子；权值较小的一组，每个粒子只生成一个新粒子。这样做不但简化了计算，提高了运行速度，而且增强了重采样粒子的有效性。
该改进算法的优点：(1)使得后验分布样本更加接近真实分布；(2)大大减少了计算量。多次实验表明，改进算法在人体运动跟踪时较传统算法效果更好，鲁棒性更高。
2 基于改进粒子滤波算法的人体运动跟踪
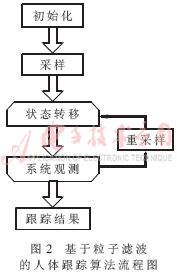
视频中的特定人体有其独特的运动特征，且其关节运动都是非刚性的。为使运动模型在运动预测中有更好的适用性和更高的准确性，依据统计分析的成果，采用一阶自回归过程ARP（Auto-Regressive Process）动力学模型作为运动模型，并通过训练序列计算出该模型的参数。在模板区域相似性计算的基础上，通过粒子滤波实现人体运动的跟踪。基于这一基本思路，本文提出基于粒子滤波的人体运动跟踪的流程图，如图2所示。
2.1 初始化
跟踪初始化，就是按运动模型的要求，在初始帧形成表示各自分布模型的粒子集。具体过程如下：在被跟踪序列的初始帧中手动提取目标模板，将它作为起始帧的状态向量。提取目标的初始运动参数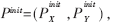
在状态向量的各分量上加正态随机噪声，构造N个状态向量，即粒子数为N，每个粒子代表一个可能的运动状态。若初始的权值ωi为1，则具有N个运动状态参数
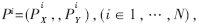这里Pi选择Pinit附近的点。
2.2 采样
采样就是从表示先验模型的状态向量集中按概率选取其中的若干向量。一次采样选取一个状态向量，进行N次这样的采样，得到N个新的状态向量。显然，权值太小的状态向量(即粒子)在采样过程中被选中的概率就小，而且在逐步迭代中可能被丢掉；权值大的粒子被选中的概率就比较大，也可能被多次选中。这样，采样得到的新的粒子集能更好地估计概率分布。
2.3 状态转移
系统状态转移，即粒子的传播过程。从采样得到的新的粒子集出发，经运动模型计算得到预测模型。粒子传播是一种随机运动过程，服从一阶ARP方程。
式中，xt为目标在t时刻的状态，wt-1是归一化噪声量，A和B是常数。这里，t时刻系统的状态转移过程与当前时刻的观测量无关。
粒子Ni的运动状态参量为：
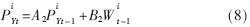
式中，A1、A2、B1、B2为常数，一般A取1，B为粒子传播半径（系统状态转移过程中，粒子所能够传播的范围），W是[-1，1]内的随机数。系统状态转移的实质就是在坐标上迭加一个扰动量。
这一步是先验概率的传播过程，即“假设”目标状态将以何种方式传播。粒子传播是否合理需要通过下一阶段即系统观测进行验证。
2.4 系统观测
系统观测过程就是将当前预测模型中的每一个状态向量所对应的外观模型与由其确定的当前帧图像中的对应区域进行相似性计算，并给每一个状态向量赋一个权值。
每个粒子状态转移后，用对应新坐标计算一个MADi。
定义概率密度函数为：
它作为当前帧的跟踪结果输出。
2.5 重采样
按上述采样、转移和观测过程完成当前帧的跟踪计算后，对当前帧的后验模型进行同样的采样，得到下一帧的先验模型。进而可以对下一帧进行新的预测和观测，继续后续序列的跟踪计算，直至最后一帧，完成跟踪过程。
3 实验仿真和分析
3.1 仿真结果
按照上述步骤，使用C语言在VC环境下编译，实现本文算法框架。为了验证该改进算法的有效性，对一组在走廊内拍摄到的行人视频序列进行跟踪（右边行人为跟踪目标）。序列长度为1376帧，每帧图像的大小为384×288，选取207～407共200帧进行仿真。207帧作为初始模版，跟踪人体的目标大小为30×70，如图3所示。每幅图像对应的帧分别为：207，242，265，287，310，331，356，361，407。
实验跟踪结果表明，本文提出的基于改进粒子滤波算法的人体运动跟踪在强杂波背景下，对人体产生遮挡和自遮挡时的跟踪是有效的和稳健的，有很好的实际应用价值和推广价值。
3.2 结果分析
为了进一步说明该改进算法的优越性，将原始视频序列、改进算法跟踪序列、传统算法跟踪序列进行比较，如图4所示。
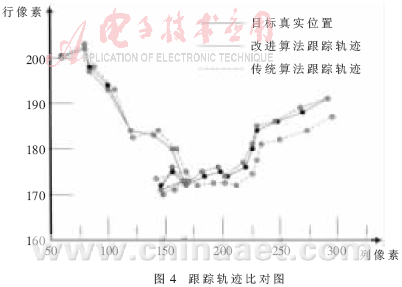
图中三条曲线是对三组视频序列每隔20帧取样、描点、连线所得，分别反映了目标真实的运动轨迹和两组跟踪轨迹。如图所示，改进算法始终准确地跟踪到目标，而传统算法跟踪精度相对不高，且随着时间的推移产生了漂移现象。
视频人体运动跟踪是计算机视觉领域一个重要研究方向。本文结合局部最优化原理对粒子滤波算法的系统观测环节和重采样环节加以改进。将改进算法引入人体运动跟踪获得了令人满意的效果。视频人体运动跟踪在众多领域都有着广泛的应用，所以该新算法的提出有广泛的应用前景和推广价值。但该问题的研究尚未成熟，需进一步完善。
参考文献
[1] CHAM T J，REHG J M.A multiple hypothesis approach to figure tracking//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition，Fort Collins，Colorado，1999，239-245.
[2] ARULAMPALAM M，MASKELL S，GORDON N，et al.A Tutorial on Particle Filters for Online Non-linear/NonGaussian Bayesian Tracking[J].IEEE Trans on Signal Processing，2002，50(2)：174-188.
[3] 胡士强，敬忠良.粒子滤波算法综述[J].控制与决策，2005，20(4)：361-365.
[4] BRUNO MG S.Bayesian methods for multi aspect target tracking in image sequences[J].IEEE Trans on Signal Processing，2004，52(7)：1848-1861.
[5] LI P H，ZHANG T W.Visual contour tracking based on sequential importance sampling/resampling algorithm[C]//Proc of the 16th Int.Conf.on Pattern Recognition.Canada：IEEE Computer Society，2002，2：564-5681.
[6] 李华.基于概率模型的三维人体运动研究[D].中国科学院研究生院智能信息处理重点实验室，2005.
[7] FISHER R.CAVIAR test case scenarios.2003.http：//homepages.inf.ed.ac.uk/rbf/CAVIAR.