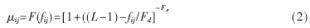
通常取F_e=2，Fd可由渡越点确定。然后对图像进行增强，采用的非线性变换函数为：
   
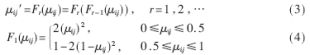
    最后对μ_ij′进行反模糊化处理，得到经过模糊增强后的图像f′，f′中的像素点f′(i，j)的灰度值f_ij′为：
      

式中，F^-1(g)为F(g)的逆运算。
    由参考文献[6]可得到如下结果：(1)经过式(3)的Fr(g)变换后，会出现μ_ij′ij的最小值）的情况，此时F^-1(g)的逆变换无解，Pal算法中对μ_ij′ij′=a。这样会造成在增强后的图像f′中，原图像f中相当多的低灰度值被硬性切削为零，从而损失了f中的部分灰度信息，影响边缘检测质量。(2)由于变换F(g)和F^-1(g)的函数复杂，计算量大，影响处理速度。(3)对渡越点fc的选取是随机的，并需要人工介入，缺乏理论指导。
1.2 新模糊图像增强算法
1.2.1 广义模糊增强算子
    为克服上述缺陷，根据广义模糊集合具有比普通模糊集合更大的拉伸和变换范围等优点，本文定义一种新的广义模糊增强算子，并对模糊图像增强算法的核心函数式(2)～(5)进行了如下修改：
   
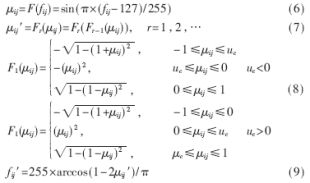
式(8)中，μ_c是由渡越点f_c确定(fc可由OTSU算子自适应获得)。解决渡越点选择需要人工介入的缺陷，消除了渡越点选择的随机性。则μ_c的值不一定等于0.5，其公式为：
   
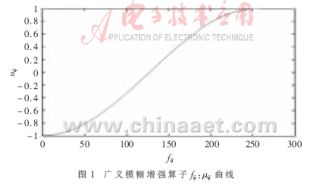
    F_r(μ_ij)随着?滋ij的值不同而增大（当μ_ij>μ_c）或减小（当μ_ij≤μ_c）。当μ_ij>μ_c时，非线性变换的结果使μ_ij′的值向1靠近，从而使得f_ij′向L-1靠拢；反之，当μ_ij≤μ_c时，非线性变换的结果使μ_ij′的值向0靠近，从而使得f_ij′也向0靠拢。广义模糊增强算子f_ij：μ_ij变化曲线如图1所示。
    由图1可知，μ_ij取值范围为[-1，1]，经过式(8)非线性增强后,μ_ij′取值范围也为[-1，1]，解决了非线性变换和逆变换后局部无解所造成的图像部分灰度信息丢失的问题。

                  
1.2.2 图像增强算法步骤
    图像的边缘信息是梯度突变的区域，文中定义为敏感区域。在进行图像增强时，通过梯度算子先确定出敏感区域的像素点，然后再利用广义模糊增强算子对敏感区域的像素点进行模糊图像增强处理，同时通过OTSU算子自动计算最佳渡越点。由于只是对敏感区域的像素点进行模糊图像增强运算，从而减少了大量不必要的运算，提高了处理速度。相关的算法步骤如下：
    (1)采用梯度算子求出图像敏感区域的像素点。设图像f，像素点f(i，j)的梯度可以表示成一个矢量，设G_i、G_j分别表示像素点f(i，j)沿着i方向和j方向的梯度，则这个梯度矢量可以表示为：
   

    这个矢量的幅度可以表示为：
     

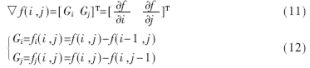
    适当选取门限μ，令θ=25。对于像素点f(i，j)，若mag(f)>θ时，则将其标记为敏感区域的像素点，记为f_s(i，j)。
    (2)采用OTSU算子求出图像fs区域的最佳阈值T。
    (3)利用文中提出的广义模糊增强算子对图像敏感区域fs进行图像增强处理。
    通过步骤(1)得到的结果，首先去掉了图像非边缘（不属于f_s）的像素点，将这些像素点直接标记为背景，再由步骤(2)得到最佳阈值T，并结合式(10)求出广义模糊增强算子的渡越点：
       

    由式(6)对图像敏感区域f_s进行模糊化处理，映射为特征平面上的模糊矩阵，然后由式(7)和式(8)进行非线性变换，对特征平面矩阵数据进行增强处理，最后由式(9)将处理后的矩阵数据进行反模糊化处理，映射到图像空域中去。
2 边缘提取算法
    设图像f中的像素点的灰度值为f(i，j)，b(i，j)是结构元素。用b对f进行灰度腐蚀与膨胀定义为：
   

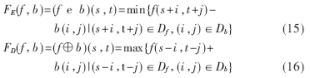
式中，D_f和D_b分别是f和b的定义域。
    对灰度图像进行膨胀得到结果与进行腐蚀得到的结果相减其结果称为形态学梯度，定义为：
        

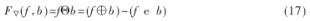
    为了更好地提取出不同方向的边缘，定义四种不同方向的3×3的结构元素，如图2所示。

               
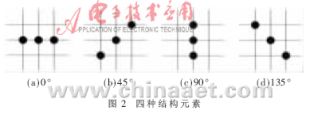
    四种结构元素分别为：B₁=((-1，0),(0，0)，(1，0))、B₂=((-1，1),(0，0)，(1，-1))、B₃=((0，-1),(0，0)，(0，1))、B₄=((-1，-1),(0，0)，(1，1))。
    数学形态学边缘提取算法为：对图像敏感区域f_s像素点f_s(i，j)依次从四个方向进行数学形态学梯度处理，设A为以f_s(i，j)为中心的1×3的区域集合，可得处理结果为：
   
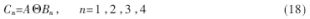
    由式(18)可得图像的总的梯度结果集合为C=C₁∪C₂∪C₃∪C₄，即：
    

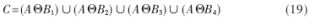
    同时用OTSU算子重新计算最佳阈值T′来对C内的像素点f_s(i，j)进行阈值化分割，如下式：
   

    可得到结果C′为：
     

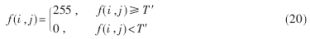
    集合C′即为提取出的边缘。
3 实验结果与分析
    在相同的硬件和软件资源环境下，实现上面各种图像处理算法。实验的硬件平台为P4 2.40GHz处理器和256MB内存的工控机，软件开发环境为Visual C++ 6.0。实验采用256级沥青路面裂缝灰度图像（采集于西安—宝鸡高速公路），大小为800×500个像素，背景光照不均并且含有大量的噪声。对如图3(a)所示的样本图像分别采用Pal算法、参考文献[4]算法以及文中提出的图像增强算法进行增强处理，渡越点通过OTSU算子运算统一确定为146，并且各种增强算法仅进行一次迭代处理，最后，结合文中提出的边缘提取算法对增强后的图像进行边缘提取，其结果如图3(b)、(c)、(d)所示。

                 
    由图3可以看出，三种" title="三种">三种模糊图像增强算法对裂缝边缘的增强和保护效果都很好，但因受噪声的干扰，Pal算法和参考文献[4]算法在增强裂缝边缘的同时，对噪声也进行了增强，不能很好地抑制噪声。而本文提出的图像增强算法在增强和保护裂缝边缘的同时，很好地抑制了噪声，如表1所示。由此说明本文提出模糊图像增强算法具有很好的边缘增强能力和很强的抗噪能力。

                  
    在程序中利用“time”类的Clock( )函数来计算并比较三种模糊图像增强算法对样本图像进行一次迭代图像增强所需的运算时间，如表2所示。

                   
    由表2可以看出，本文提出的图像增强算法对样本图像进行增强所需的处理时间最短。说明了其在保证增强处理的效果的同时，也保证了处理速度。
    采用本文提出图像增强算法对样本图像进行增强处理，再分别采用Sobel算子和Prewitt算子进行边缘提取，其效果如图4所示。

                     
    对比图3(d)和图4，可以看出，Sobel算子和Prewitt算子提取出的裂缝边缘有断裂现象和大量的噪声，并且将路面中的标志线也提取出来，不利于后期对裂缝进行分析；而本文提出的边缘提取算法能很好地抑制噪声，较好地提取出裂缝边缘和保护裂缝边缘的完整性，并且提取的裂缝边缘光滑，极大地方便后期对裂缝进行分析。同时，利用“time”类的Clock( )函数来计算并比较三种边缘提取算法，对样本图像进行边缘提取所需的处理时间如表3所示。

                   
    由表3可以看出，本文提出的边缘提取算法对样本图像进行边缘提取所需的处理时间最短，说明其在保证边缘提取的效果的同时，也保证了处理速度。
    本文提出的广义模糊增强算子，解决了模糊增强算法在非线性变换后图像部分灰度信息丢失的缺陷，并将图像增强处理集中在敏感区域，大大提高了处理速度，同时，通过程序自动计算出最佳阈值参数，克服了阈值参数选择的盲目性，具有一定的自适应性。最后，结合数学形态学边缘提取算法对图像进行边缘提取，应用于沥青路面裂缝图像检测系统中。实验结果表明，文中提出的图像增强和边缘提取算法能够很好地增强裂缝边缘信息和保护裂缝边缘的完整性，并且具有很好的抗噪能力和实时性，有一定的实用性和推广性。
参考文献
[1] PRATT W K.Digital image processing(2nd edition)[M].New York，USA：Wiley Interscience，1991：188-198.
[2] PAL S K，KING R A.Image enhancement using fuzzy sets[J].Electron.Lett.，1980，16(9)：376-378.
[3] PAL S K，KING R A.Image enhancement using smoothing with fuzzy sets[J].IEEE Trans.Syst.Man.Cybern.，1981，11(7)：494-501.
[4] 李弼程，郭志刚，文超.图像的多层次模糊增强与边缘提取[J].模糊系统与数学，2000，14(4)：77-83.
[5] 李晋惠.用图像处理的方法检测公路路面裂缝类病害[J].长安大学学报(自然科学版)，2004，24(3)：24-29.
[6] 王保平，刘升虎，范九伦，等.基于模糊熵的自适应图像多层次模糊增强算法[J].电子学报，2005，33(4)：730-734.