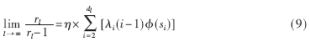基于LDPC码不等保护特性改进的混合重传算法
2008-07-22
作者:李振松, 李学华, 杨大成
摘 要: 提出了一种基于非规则LDPC码的不等保护特性" title="保护特性">保护特性改进的混合重传算法UEPB-HARQ(Unequal Error Protection Based HARQ)。通过合理设计LDPC码的校验矩阵,提出了一种整体考虑不同度节点对应重传比例的基于不等保护特性的混合重传算法,从而获得更好的传输性能。
关键词:非规则低密度奇偶校验码 度分布 不等保护特性 基于度分布的混合重传技术
LDPC码(Low-Density Parity-Check Code)[1]是一种校验矩阵为稀疏矩阵的线性分组码。由于LDPC码,特别是非规则LDPC码在AWGN信道下具有接近香农极限的性能,同时具有随码长增加而线性增加的译码复杂度,因此受到越来越多研究者的关注。
度分布(λ, ρ)是LDPC码最重要的性能参数[2,3]。对非规则LDPC码来说,度越大的节点与之相连的校验节点就越多,也就可以获得更准确的消息。这些节点通过校验矩阵将正确的消息再传到度低的节点,最终提高成功译码的概率,这就是LDPC码的不等错误保护UEP(Unequal Error Protection)特性[4]。利用这个特性,通过对不同度节点选择合适的比例进行重传,可以改善系统的传输性能。
参考文献[5]中提出了一种基于度分布的HARQ技术,通过重传尽可能大的度节点来获得系统的增益。本文在此基础上,通过合理设计LDPC码的校验矩阵,并根据高斯" title="高斯">高斯近似法,对所有度节点进行整体考虑,给出合理的重传比例,实现系统性能" title="系统性能">系统性能的最优化。
1 算法描述
LDPC码可以用校验矩阵或者是相应的Tanner图[5]来表示。在LDPC码的校验矩阵中,每列所有元素中1的个数称为该列对应的信息节点的度;每行所有元素中1的个数称为该行对应的校验节点的度。
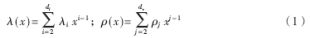
其中λi和ρj分别是度为i的变量节点和度为j的校验节点对应的1的个数占校验矩阵中总的1的个数的比例。dl和dv分别是变量节点和校验节点对应的最大" title="最大">最大度。
如果码长为N,则对应Tanner图中度为i的节点的个数为:

然后按度的不同把所有节点划分到不同的子包中,各个子包对应特定度的节点。在重传时,包含度为i的节点的子包对应的重传比例为pi,它表示重传数据中度为i的节点个数占重传节点总数的比例。定义为:

其中ti表示度为i的变量节点的重传个数,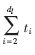 表示一次重传所传输的总的节点个数。
表示一次重传所传输的总的节点个数。
当收到重传请求时,发送端就根据重传比例在相应的子包中取出相应数量的节点组成重传数据进行重传。接收端再将接收到的重传数据与先前收到的数据进行合并,并再次尝试译码,直到译码成功或者达到最大重传次数。
为能获得最好的性能,需要给出特定的重传比例pi。以下的分析表明本文提出的算法可以获得最佳的重传比例,从而获得最优的系统性能。
2 性能分析
在AWGN信道中,调制方式为BPSK调制时,得到信道模型为:
y=x+n (4)
其中,x∈{±1}为发送信号,n是均值为0、方差为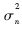 的高斯噪声,y为接收信号。
的高斯噪声,y为接收信号。
对此,可以运用高斯近似(GA)来分析算法的渐进性能。根据参考文献[4],高斯近似的结果为:
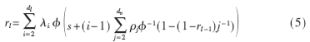
其中,rl=mvl是第l次迭代后输出信号的均值,初始值为r0=φ(s0),其中
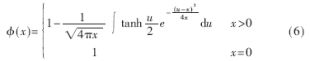
根据GA,如果当l趋于无穷时,rl收敛到0,则LDPC码的译码错误可以任意小。
等式(5)是一个关于rl的迭代式。当迭代次数l趋于无穷时,rl会减小并收敛到一个常数,而当SNR大于门限值时,这个常数将为0。
由pi是度为i的变量节点对应的重传比例,因此相应的初始状态为:

由于信道初始信息可以通过(7)式对接收到的子块进行软合并而增大,因此重传可以通过降低门限值来加快收敛速度。
在DDB-HARQ中,先前收到的译码失败的信号并不直接丢弃,而是和新收到的重传信号进行软合并。经过HARQ接收机软合并后,根据参考文献[5],(5)式可化简为:
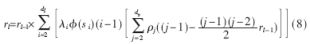
其中, 和i无关。
和i无关。
由(9)式可知,当l趋于无穷时,rl是一个几何级数。它的值只与λi和si有关。其中si是信道信息,和选择的方式无关,而λi对于特定的度分布也是常数。因此,rl可以写成:

其中,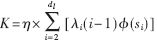 。
。
从(10)式可以看出,K越小,门限值收敛的速度越快。为了提高重传的功率效率,应该找到尽可能小的K和相应的si,所以要研究在什么情况下K会取得最小值。令:

根据(7)式,(11)式可以写成:
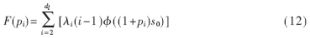
的pi,使得(12)式取得极小值。根据这个优化模型,得出的pi就是最佳的重传比例。
由于(12)式是一个多约束条件下求极值的问题,无法得出闭式解。但是可以运用数值计算的方法求出特定度分布所对应的F(pi)的极小值,从而得出最佳重传比例pi。
根据参考文献[8],?准(x)可以简化为:

将这个简化式代入" title="代入">代入优化模型,通过数学建模软件,比如说LINGO,运用数值迭代的方法得到pi的数值解。由于该优化模型从整体上考虑了所有度节点对译码的贡献,因此利用优化结果所得的pi值进行重传,就可以使得系统达到最大的重传功率利用率,从而获得最好的系统性能。
3 仿真及结果分析
在仿真过程中,采用的非规则LDPC编码的度分布为:

采用的码长N=1 024,码率为R=1/2。每次重传的比特数为256。通过LINGO优化软件,根据优化模型,可以得到表1所示的最佳重传比例。

从表1中可以看出,优化的比例并不只是重传度大的节点,同时也是重传度较小的节点。这可以理解为:虽然有些度比较小,但是它对应的比例很大,这样在整个译码过程中可以提供很多的信息量,所以在重传节点中包含这些节点必然会增加重传后译码成功的可能性。
本文在仿真中每次重传256个比特,重传比例为1/4。改善的DDB-HARQ重传算法各个度对应的重传比特数由表1中的ti给出。只有重传度较大的算法是从发送信号中取出256个度和最大的节点进行重传。
图1是最大重传次数为1次时的误码率曲线。从图中可以看出,采用重传技术后误码性能有明显的改善。改进的DDB-HARQ方案在高信噪比下比只重传最大度节点的方案性能增益更大。这是因为在信噪比较大时,度大的节点正确接收的概率已经很大,重传后得到的额外信息量并不大,而改进的算法由于包括各个度的节点,因而性能还能进一步提高。
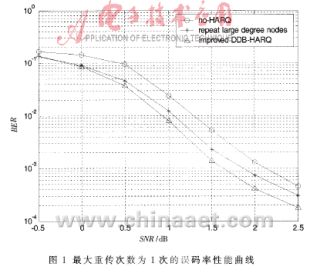
图2是最大重传次数为3次时的误码率曲线。从仿真图中可以看出,改进的DDB-HARQ算法比只重传度大的节点的系统性能有明显的改善,说明经过优化的重传比例确实改善了重传效率。重传次数为3次比重传次数为1次有更大的性能增益。这是因为重传次数增加后,译码器可以更确切地掌握对译码帮助最大的接收信息,从而提高译码的成功率。

本文通过对非规则LDPC码运用高斯近似,给出了基于LDPC 码不等保护特性的重传方式的系统性能的优化方法。仿真结果表明本文提出的改进的基于度分布的重传算法,能充分利用非规则LDPC码的不等保护特性,提高重传的效率,改善系统的传输性能。
参考文献
[1] GALLAGER R G. Low density parity check codes [J]. IRE Trans. Inform. Theory,1996,(8):21-28.
[2] LUBY M G,MITZENMACHER M, SHOKROLLAHI M A. Improved low-density parity-check codes using irregular graphs[J].IEEE Trans on Information Theory. 2001,47(2):
585-598.
[3] MACKAY D, WILSON S, DAVEY M. Comparison of constructions of irregular gallager codes. IEEE Trans. Commun, 1999,47(10):1449-1454.
[4] CAO Yi Qing, GU Jian, QI Lin, et al.Degree distribution based HARQ for Irregular LDPC. Electronics Letters.2006,42(3):363-364.
[5] TANNER M. A recursive approach to low complexity codes. IEEE Trans. Inform. Theory, 1981,IT-27(9):533-547.
[6] CAMPELLO J. MODHA D S. Extended bit-filling and LDPC code design. Global Telecommunications Conference, 2001. GLOBECOM '01. IEEE Volume 2,
2001,2(25-29):985-989.
[7] RICHARDSON T J, SHOKROLLAHI A, URBANKE R L.Design of capacity approaching irregular low density parity check codes. IEEE Trans. Inform. Theory,2001,IT47:619-637.
[8] CHUNG S Y, RICHARDSON T J, RUDIGER L U.Analysis of sum-product decoding of low-density-parity-check codes using a gaussian approximation, IEEE Trans. Inform. Theory,2001,47(2).