滤去图像噪声的同时保持其中的细节是图像处理的一个重要内容。现实中由于照相机的性能和光线强弱的变化，噪声在图像中不可避免。去除噪声的方法大致分为两类，即线性方法和非线性方法。线性滤波和含噪图像的卷积能有效地去除高斯噪声以及其它呈均匀分布的噪声，但此方法把边界处灰度变化较大位置的点也当作椒盐噪声处理，因此它对这种噪声效果甚微，并且还经常造成图像模糊。为了克服上述问题，采用非线性滤波。中值滤波是最常用的方法。当考虑一个小邻域时，椒盐噪声能得到高效的抑制。然而中值滤波的最大缺点是它作用于整幅图像，会损失其中的大部分细节。寻找一种既能有效去除噪声又能保持细节的方法是许多人感兴趣的问题。
　　为了解决这个问题，已研究了不少基于中值滤波的改进方法。近来开关中值滤波引起许多人的注意，因为它在滤波之前首先对脉冲噪声进行探索，从而较好地避免了对未污染像素的修改^[1～3]。开关中值滤波^[1～2]用中值来探索噪声点，算法实现比原来的方法简单有效；然而基于中值的椒盐噪声探索不能把细线从椒盐噪声中区分开，细线也被看成噪声被除掉。当图像中噪声密度较高时，排序均值去噪效果不错，但计算复杂度比较高^[3]。基于拉普拉斯算子和模糊逻辑" title="模糊逻辑">模糊逻辑的中值滤波能较好地保持图像的细线和细节特征，但计算量比较大；而基于拉普拉斯算子和非模糊逻辑的中值滤波却不能实现压抑噪声和保护细节的平衡^[4]。本文采用基于多方向的非模糊逻辑中值滤波，能较好地维持图像的细线和细节特征，并且算法实现也比较简单。
1 噪声探索
　　在开关中值滤波中，噪声探索决定被检验点是否为噪声点；如果此点是噪声点，那么滤波值定为中值滤波的输出值，否则此非污染像素点就不通过中值滤波，按原来的值输出。显然椒盐噪声的探索决定着开关中值滤波的滤除效果。
　　椒盐噪声点的探索通常假定噪声点的灰度值比周围的大或小。若x_ij和y_ij分别代表图像中(i,j)点的污染像素值和滤波后的像素值，常用的中值滤波输出值即为中心在x_ij、大小为(2N+1)×(2N+1)的窗中排序元素的中值，即：
　　
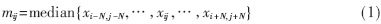
　　为了判断x_ij是否为噪声点，基于中值的椒盐噪声探索计算差值d=x_ij-m_ij，然后用一个预先设定的阈值T与d做比较：
　　
　　当α_ij＝1，x_ij为噪声点；否则x_ij为非噪声点，这种滤波的输出结果为：
　　
　　这种基于中值的开关滤波的缺点就是不能把图像中的细线从椒盐噪声中区分出来，而把细线当作噪声除去。
　　基于拉普拉斯的开关中值滤波首先将原图像和四个一维的拉普拉斯核作卷积，每个卷积结果对边界都比较敏感，这四个卷积结果的最小值r_ij用来探索噪声点。这是因为：(1)当x_ij为椒盐噪声点时，四个卷积结果都相当大，r_ij也比较大；(2)当x_ij为非椒盐噪声点时，四个卷积结果都较小趋于零，r_ij也较小；(3)当x_ij为边界(包括细线)上的点时，四个卷积结果中有一个较小(趋于零)，其余三个可能比较大，r_ij也比较小。因此可以用r_ij和一个阈值做比较来探索该点是否是噪声点，即：
　　
　　然后用(3)式来计算滤波结果。用(3)式和(4)式结合的滤波即为基于拉普拉斯的非模糊逻辑中值滤波。这种算法不能较好地实现压抑噪声和维持细节的平衡，当椒盐噪声被滤除掉时，很多细节却被模糊；当保留相当多的细节时，不少的椒盐噪声又被残留。若把α_ij看成定义于0与1之间的r_ij的连续函数，α_ij可解释为x_ij为噪声点的可能性大小。模糊逻辑原则为：当r_ij的值较大时，α_ij也较大；当r_ij的值较小时，α_ij也较小；此原则结合(3)式为基于拉普拉斯的模糊逻辑中值滤波。本文在基于拉普拉斯的非模糊逻辑中值滤波基础上又增加了两个卷积核，然后取这六个卷积结果中的最小值r_ij和设定的阈值T做比较，
　　
　　其中Kp表示第p个核，?茚表示卷积运算，这p个核如图1所示。

　　这样，关于被检验点x_ij比原来的方法考虑了更多的邻域信息，因此探索椒盐噪声的能力更高一些；考虑到在维持细节的同时，残留的噪声主要集中在图像的平坦部分，因此在图像较平坦的地方用了较小的阈值T1，而在其它地方用较大的阈值T2。采用式(5)中的方法判断出图像的平坦部分，先对所考虑的窗中元素进行递增排序，然后计算下式：
　　
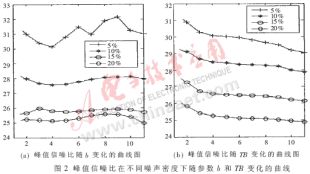
　　其中b为位移偏移量(正整数)，TB为阈值。如果距离排序后窗口内两个极值一定距离b的两点的灰度差在TB内，则判断x_ij为平坦区域的像素点。对参数b和TB的选取将通过试验得到。下面以cameraman图像为例给出峰值信噪比" title="信噪比">信噪比在不同噪声密度下(分别为5%、10%、15%和20%)随参数b和TB变化的曲线，如图2。多个实验结果表明，其分布曲线相似。
　　从图2可以看出，当噪声密度为5％时，峰值信噪比随b的变化较剧烈，其它情况下变化比较平稳，综合不同噪声密度下的变化曲线，b等于9，试验效果最好。

　　参数TB的选取从图2中很容易看出，当TB>2峰值信噪比明显下降，TB等于2是最佳的选择。
2 实验结果分析和比较
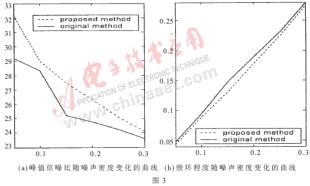
　　以分辨率为256×256的 cameraman图像为例将基于拉普拉斯的非模糊逻辑中值滤波方法(一)和本文建议的方法(二)进行比较。在方法(一)仿真试验中，选取的阈值T=200左右；方法(二)中较大的阈值T2比T略大一些，较小的阈值T1在150左右，T、T1和T2的取值都随噪声密度的增加而减小。图3给出了在噪声密度为5%、10%、15%、20%、25%、30%情况下用这两种方法处理后图像的峰值信噪比PSNR和对原图像的毁坏程度分别随噪声密度变化的曲线。从图3中容易看出，本文建议方法的峰值信噪比比原来的方法有名显的提高，并且对图像的毁坏程度也比原来的方法有所降低，较好地实现了压抑噪声和维持细节的平衡。图4为当噪声密度为5%时用本文建议的方法(二)和原来的方法(一)对cameraman图像(256×256)滤波后的比较图。从图4的视觉效果来看，用方法(二)处理过的图像与原图像基本一致，因为此时噪声对原图像的毁坏程度仅有4.3％。

　　本文对基于拉普拉斯的非模糊逻辑中值滤波进行了改进，首先根据灰度值把图像大致分为平坦部分与非平坦部分，然后在这两个不同的部分采用不同的阈值；在对噪声的探索中又增加了两个卷积核，取这六个卷积结果中的最小值和设定的阈值做比较，能比较有效地对椒盐噪声点进行探测，较好地保留了图像中的细线和细节特征。