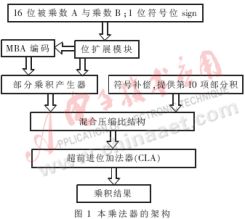
乘法是数字信号处理中的基本运算。在图像、语音、加密等数字信号处理领域中，乘法器扮演着重要的角色，并在很大程度上左右着系统的性能。如何以最少的资源实现乘法器的最高速度将成为乘法器的主要研究方向。由于树型结构模块是阵列乘法器设计中的瓶颈，本文在深入研究了乘法器的体系结构，并比较了各种树型结构的基础之上，提出了一种适合于16×16有/无符号数乘法器的混合压缩比结构。并且基于该结构同时采用改进布斯算法、符号扩展技术设计出了一个16×16有/无符号数乘法器，其架构如图1所示。

1 改进布斯算法与布斯编码设计
　　在高速乘法器的设计中广泛应用的是改进布斯算法(Modified Booth Algorithm, MBA)，也称为基4(Radix-4)布斯算法。该算法通过对乘数重新编码和压缩部分乘积项" title="乘积项">乘积项(PP)的数目来提高运算速度。而压缩率则取决于编码方法，如果采用三位MBA编码，则可以压缩一半的PP^[1]，大大提高了运算速度。
　　MBA编码原理如下：对于有符号数乘法运算A×B，若乘数B的长度为奇数，则需要高位扩展一位符号位使乘数的位数是偶数；若乘数B的长度为偶数则不用高位扩展。设扩展后乘数B的长度为N位，这时N是偶数，乘数B可写为：

　　这样，N位的乘数B将会产生N/2个部分乘积项。
　　改进布斯编码规则是：首先对乘数的最低位额外增加一位(B_[-1]=0)，然后每次取乘数的偶数位(B[0]，B^[2]，B^[4]，… )以及相邻的奇数位(共三位)进行编码。这样E＜i＞的取值为0，±1,±2，然后再与被乘数A相乘，得到对应的部分乘积项是(0，＋A，－A，＋2A，－2A)，这五种操作需要3位的布斯状态码进行识别。
　　在本设计中，布斯状态码所采用的逻辑关系如下：
　　PN=BH
　　ONE=(~BR)&BL∣ BR&(~BL)=BR⊕BL                              (3)
　　TWO=(~BH)&BR&BL∣ BH&(~BR)&(~BL)
　　= (~BH)&(BR&BL)∣BH&(~(BR∣BL))
　　式中，BH表示相邻高位，BR表示本位，BL表示相邻低位。PN为0时为加操作，为1时为减操作；ONE为0时操作数为0，为1时操作数为A；TWO为0时操作数为0，为1时操作数为2A。
　　如图1所示，本乘法器的输入量为1位符号标志位sign，用于标识有/无符号数以及16位被乘数A与乘数B。首先根据符号标志位sign将被乘数A与乘数B都转换为17位的有符号数。由于布斯编码需要乘数宽度N为偶数，故对乘数B再进行1位高位扩展，因此该乘法器实际操作数变成了17位×18位。由式(1)可知，对18位的乘数进行改进布斯编码会产生9(18/2)个部分乘积项。
2 符号补偿技术
　　在乘法器树型求和过程中，为了使各个部分乘积项对齐，将需要大量的符号位扩展操作。因为部分乘积项的符号位可能是1或者0，所以扩展存在不确定性，直接扩展会造成资源的浪费。解决的方法是采用符号补偿技术^[2]，消除符号位扩展中的不确定性，节省占用的逻辑资源，提高运算速度。
　　符号补偿算法描述如下：例如，把8bit有符号数SXXXXXXX扩展为12bit，其中S表示符号位，X表示数据位。采用符号位直接扩展时，可以得到SSSSSXXXXXXX。对其进行等价逻辑变换：
　　
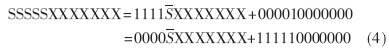
　　于是，符号位扩展转化成为：对原操作数的符号位取反，并在高位直接补0，再对式(4)中第二项的确定部分进行补偿。
　　为了简化电路，对前面产生的九个PP所需的位扩展进行一次性补偿，补偿项就构成第十项部分积，也就是说对每个PP的位扩展都采用符号补偿技术，并把所有的补偿项预先加好，用补偿向量V表示，其求导过程如图2所示，得到V=11010101010101011。

3 混合压缩比树型结构及乘法器仿真与下载
　　在对部分积求和的过程中，重复阵列IA结构与Wallace树结构是两种典型的压缩结构。IA结构规整，采用串加的形式，利于产生版图，但速度较慢；Wallace树结构采用并行结构，可将求和级数从O(N)降为O(log2N)，大幅提高运算速度^[3]，但缺点是布线困难。两种结构都不适合实际应用。因此，大多采用折中的策略^[4～7]把二者结合起来，使乘法器在速度和占用资源两方面都有较好的性能，例如ZM树结构和OS树结构等。
　　对于16位×16位有/无符号数乘法器，由上所述，总共有10个部分乘积项，需要通过某种树型结构压缩为两项，即需要一个10-2压缩器，再通过超前进位加法器得到最终乘积结果。IA阵列的结构如图3所示，Wallace树结构如图4所示。在比较各种树型结构的基础上，本文提出了一种适合于16×16有/无符号数乘法器的改进树型结构，即混合压缩比结构，如图5所示。

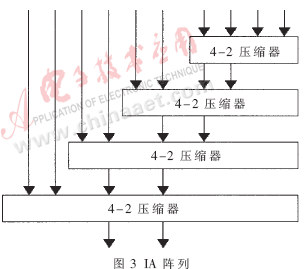
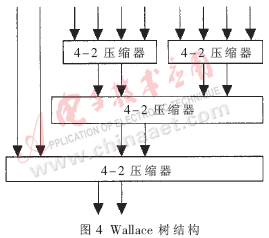
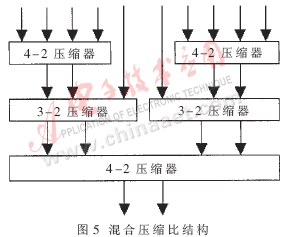
　　各图中的4-2压缩器，也称为5-3加法器，功能是将四个输入量压缩为两个输出量。其代数运算式为：D +C×2+C_o×2=I₀+I₁+I₂+I₃+C_i。在本设计中采用的输入输出逻辑关系如下：
　　
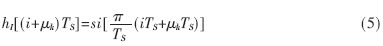
　　混合压缩比结构中的3-2压缩器也称为保留进位加法器(CSA)，其功能是将三个输入量压缩为两个输出量。3-2压缩器的输入输出逻辑关系为：
　　
　　分别按照图3～图5的树型结构设计出对应的乘法器，再对这三种乘法器的性能进行比较。由于构成乘法器的其它模块相同，所以整个乘法器占用资源多少与延迟大小的区别完全取决于各自所采用树型结构的性能优劣情况。
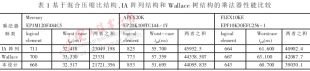
　　在QuartusII环境中分别对这三种乘法器进行系统级的仿真比较，结果列于表1中。其中，logical element参数反映所设计乘法器占用的资源，Worst-case tpd参数反映乘法器的速度性能，两者之积可以反映乘法器的综合性能。从仿真结果可以看出，采用Mercury EP1M120F484C5与FLEX10KE EPF10K30EFC256-1芯片，混合压缩比结构乘法器占用资源与速度的性能都优于IA乘法器和Wallace树乘法器；而采用APEX20K EP20K100TC144-1V芯片，混合压缩比结构乘法器虽然占用资源较多，但是速度最快，资源与延迟二者之积仍为最小。因此可以得出结论：本文提出的混合压缩比结构适合于16×16有／无符号数乘法器，优于IA结构和Wallace树结构。

　　基于混合压缩比结构的乘法器时序仿真如图6所示，时序仿真采用的芯片为主流系列的FLEX10KE EPF10K30EFC256-1。图6中所举算例为：无符号数BCD8×F794；有符号数FFFF×FFFF；无符号数A7FA×FF9C；有符号数FF00×7FFF。仿真结果验证了乘法器运算正确。需要指出的是，本乘法器移植在具体系统或者集成芯片时，其延迟将小于表中的Worst-case tpd数值。
　　最后将所设计的乘法器下载到智能型可编程数字开发系统CIC-310中，如图7所示。通过大量有/无符号数算例乘法进行硬件验证，表明该乘法器设计正确，性能验证与软件仿真相符，可用作数字系统中的乘法器运算单元。

　　本文提出了一种适合16×16乘法器的混合压缩比结构，其性能优于IA结构和Wallace结构。基于该结构所设计出的乘法器通过了软件仿真和硬件验证，可以作为单元模块移植在具体系统或者集成芯片中。所提出的混合压缩比结构还可以作为10-2压缩器应用于更高位数乘法器的设计中，具有较强的实用价值。
参考文献
1 Booth A D. A Signed Binary Multiplication Technique[J]．Quarterly Journal of Mechanics and Applied Mathematics, 1951；4(2)：236～240
2 Kwentus A Y，Hung H T，Wilson AN，et A1．An Architecture for High-performance/small-area Multipliers for Use in Digital filtering Applications[J]. IEEE J Sol Sta Circ,1994;29(2)：117～121
3 Wallace C S. A Suggestion for a Fast Multiplier[J]．IEEE Transactions on Electronic Computers, 1964；13(2):14～17
4 许 琪，原 巍，沈绪榜.一种新的树型乘法器的设计［J］．西安电子科技大学学报(自然科学版)，2002;29(5)：580～583
5 Wen-Chang Yeh, Chein-Wei Jen. High-speed Booth En-coded Parallel Multiplier Design[J]. IEEE Transactions on Computers, 2000;49(7):692～701
6 K.H.Cheng et al. The Improvement of Conditional Sum Adder for Low Power Applications. Proc,11th,Ann.IEEE Int’l ASIC Conf.1998;131～134
7 Fadavi-Ardekani J.M×N Booth Encoded Multiplier Generator Using Optimized Wallace Trees, Very Large Scale Integration (VLSI) Systems. IEEE Transactions on, 1993;1(2):120～125