基于组合着色Petri网的空间复合事件检测机制
2008-07-30
作者：熊 伟, 廖 巍, 陈宏盛,
摘 要: 通过建立空间事件模型，扩展定义了空间事件复合算子及其语义；采用组合着色Petri网构造基于空间关系的复合事件检测模型并提出基于该模型的检测算法；通过应用实例验证该检测模型是一个简洁、有效的复合事件检测机制。
关键词: 空间复合事件 组合着色Petri网 复合事件检测
复合事件及其检测可以应用到股票交易、网络管理、航空交通控制、指挥决策等领域。随着空间信息的广泛应用，在远程监控、LBS、Location-aware计算等领域，也需要实现与空间有关的事件检测。传统空间信息应用系统中与空间有关的复合事件检测通过在应用处理逻辑中直接编写事件检测的代码实现。这种解决方案不利于实现开放的、可扩展的通用系统。由于很多事件是通用的，事件检测机制应该是多个应用系统共享，否则系统的维护代价较大。
对复合事件检测的研究最初是在主动数据库领域中进行的[2]。Ode采用有穷自动机实现复合事件检测。SAMOS采用着色Petri网对复合事件检测，可以携带事件流及事件参数等复杂信息。但是SAMOS也没有定义和说明Petri网的组合问题。为解决不满足交换律的复合算子的冲突问题，文献[5]引入了时序算子，提出TR-Petri网。文献[2]引入部分检测事件缓冲池和时间缓冲池对原子事件进行高效的过滤。在空间事件检测方面目前尚未展开更多的研究工作，文献[1]使用三元组{OID, TS, LOC }定义空间事件模型，支持简单的空间谓词检测，但是这种方法是基于空间对象而不是基于事件本身的空间属性。文献[4]讨论了从空间完整性约束导出数据库ECA规则的方法，由于ECA条件和动作部分可以分别在数据库中的查询处理和事务处理技术中找到相应的解决方案，而事件部分研究的不是很多。本文将在此基础上，研究基于空间关系的复合事件检测机制。
1 空间事件模型
在讨论基于空间关系的复合事件检测机制之前，首先必须形式化描述空间事件及空间事件复合算子。空间事件模型采用三元组来表示SE={EID,T,S}，其中EID∈N表示事件标识；T∈N，表示等距离离散时间信息；S∈R×R表示参照坐标系统定义的坐标。空间对象和空间谓词SP(Spatial Predicate)定义如下：
简单线段L: Sbegin×Send, Sbegin, Send∈R×R, Sbegin和Send分别表示线段的起始点和结束坐标；坐标S在线段L上时IN(S,L)为真。
封闭区域Z:∪(L×N)；坐标S在区域Z内时IN(S,Z)为真。
假设方向关系是参照坐标系统定义的，即North方向与y轴方向一致，East方向与x轴方向一致。令b表示对象的MBR，则b可以通过其左下角坐标(b.xl,b.yl)和右上角坐标(b.xu, b.yu)定义。如果以s为目标，b和s1分别是参考矩形和参考点，那么采用基于投影的方向模型，s相对于b、s1的方向关系谓词可以由North-South方向(N,S)s,b、(N,S)s,s1和East-West方向(E,W)s,b、(E,W)s,s1的组合定义。其中，(N,S)s,b和(E,W)s,b可以通过下面的公式定义，(N,S)s,s1和(E,W)s,s1可以采用类似方式定义：
如果将(N,S)s1,s2和(E,W)s1,s2的组合记作(N,S,E,W)s1,s2，那么基于四元组(N,S,E,W)s1,s2的不同取值可以定义s1相对于s2的16种方向关系，如NW(s1,s2)=(1,0,0,1)。
空间事件的语义解释函数Φ(SE):T×S→{True,False}定义为：Φ(SE(t,s))=True，if an event of type SE occurs at time t and location s。
首先将传统的事件复合算子语义扩展定义如下：
· 非空间算子NSO(NonSpatial Operator)
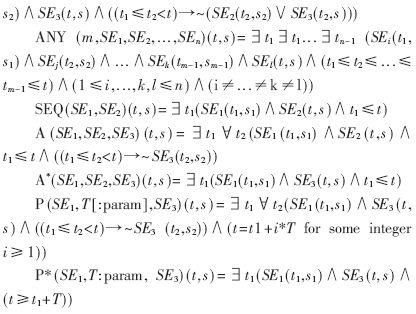
方向和距离算子有参考事件或者区域，因此这些算子是不满足交换律的。从定义来看，这些算子在时间上是以参考事件的出现为检测起始事件的。
2 基于组和着色Petri网的空间复合事件检测模型
2.1检测模型
传统的Petri网对于公共事件表达式需要构造冗余的Petri网，而且无法对位置信息" title="位置信息">位置信息进行检测，需要对之改造和扩展。本文提出基于组合着色Petri网的复合事件检测模型，既能够利用复合事件的公共表达式，也可以在存储较少事件历史的情况下，保持积聚算子。
定义(1)——复合事件检测组件Petri网CPN(Component Petri Net)
CPN的静态结构是一个八元组,CPN=(P,PI,PO,T,A, C,E,W)相关含义如下：
P是库所的有限集合。将每个原子事件对应到组件Petri网的一个输入库所，复合事件对应到组件Petri网的一个输出库所，则定义PI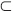
P为有限输入库所集合，定义PO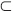P为有限输出库所集合。T是变迁的有限集合。A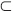P×T∪T×P是连接变迁和库所的弧的有限集合。C是标记类型(即颜色)的有限集合。E为弧函数。将每条弧映射到一个表达式、空间算子或者是缺省的单位权值" title="权值">权值。Eik表示由Pi到Tk或者Ti到Pk的弧函数。其中权值函数只作用在P×T，空间算子只作用在T×P。W: T→N变迁权值函数，将每个变迁映射到一个自然数表示的权值。
定义(2)——组件Petri网的联接变迁、联接弧及标记向量
联接变迁(Connection Transition)集合TOI为联接输出库所和输入库所的变迁，联接弧(Connection Arc)集合AOI定义为AOI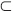PO×TOI∪TOI×PI，同时定义PTI为联接输入库所集合，PTO为联接输出库所集合。令Pi∈P，mark(Pi)=(t,s)表示Pi中当前标记的值，其分量分别标记为mark(Pi).t和mark(Pi).s。当mark(Pi).t=0时表示Pi中当前无标记。令Tk∈TOI∪T, °Tk表示Tk所有输入库所的集合, Tk°表示Tk所有输出库所的集合。
定义(3)——组合着色Petri网CCPN(Compositional Colored Petri Net)
CCPN的静态结构是CCPN=(CPN,TOI,AOI)。
定义(4)——变迁的授权
称变迁Tk是授权的，如果对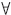
i，Pi∈°Tk, mark(Pi).t≠0。授权变迁可被触发，触发时同时执行如下三个步骤：(1)如果Pi 中标记数与Ai,k权值相等，mark(Pi)=0, 对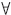i,Pi∈°Tk，如果Pi中标记数小于权值，则将标记数累加并且库所只保留最近的标记信息；(2)如果Ak,i上未定义空间谓词并且Pi中标记数与Ai,k权值相等，则mark(Pj)=Ekj(MAX{Eik(mark(Pi))|对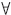i，Pi∈°Tk}), 对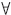j，Pj∈Tk°, 其中MAX{(a1,b1),(a2,b2),…,(an,bn)=a,b}，1≤k≤n,1≤i≤n,ai≤ak；(3)如果Ai,k上定义的SP为真，则mark(Pj)=Ekj(MAX{Eik(mark(Pi))|对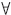i，Pi∈°Tk}), 对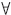j，Pj∈Tk°, 其中MAX{(a1,b1),(a2,b2),…,(an,bn)=a,b}，1≤k≤n,1≤i≤n, ai≤ak；如果Ak,i上定义的SP为假，则mark(Pi)=0, 对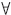i, Pi∈°Tk。
使用组件Petri网组合CCPN时，用联接弧将组件Petri网的输出库所与一个联接变迁联接，同时将该联接变迁通过联接弧与另一个组件Petri网的输入库所相联。这样的连接不会影响组件Petri网自身的触发过程，而其触发又可以带动整个CCPN的触发，从而简洁、有效地组合成了更复杂的事件检测Petri网。可以有两种方式构成CCPN，即事件作为多个复合事件的组件事件，如图1(a)；或者复合事件作为进一步复合事件的一个组件事件，如图1(b)。原子事件有可能对应到多个组件Petri网的输入库所，因此进行全局模式的事件检测时，CCPN在递归" title="递归">递归触发时需要将事件类型及其发生时刻、发生位置在网上传播。这样，对应于同样的原子事件只需要一次检测即可。对于复合事件也是一样的策略，在每个CPN输出库所中都将检测到的复合事件保存到事件链表" title="链表">链表中。
2.2 空间复合事件检测算法
构造完成CCPN模型后，本节给出全局模式下复合事件的检测算法和CCPN中标记触发并递归寻找授权变迁的算法。
算法(1)——设原子事件由数据库内核检测，则全局模式下的复合事件检测算法描述如下：
输入：原子事件
输出：检测结果链表
for all CPN which contains primitive event PE as input place
insert PE to detected list;
PE.i:= input place of PE in CPN;
for every broadcast in FindAndFire(PE.i);
for all output place of CPN
insert CE to detected list
detected list中维护当前检测到的事件链表。
算法终止性分析：首先复合事件集是有限的，并且复合事件的组件事件也是有限的，那么
(1)如果没有任何变迁触发，FindAndFire过程将终止，具体见算法(2)；
(2)FindAndFire算法递归次数有限，那么广播事件次数有限；
(3)整个算法当FindAndFire算法终止后终止。
算法(2)——CCPN事件检测算法
FindAndFire(mplace)
For each transition k
For input places of transitions k
i:=1;
Find first input place;
IF (m[i].t≠0) {
Hold the latest information or compute cumulative operator due to N[i,k]}
WHILE firing AND i ＜NP DO{
i:= i+1;
Search other input place and t:=m[i];
IF t.t = 0 {{firing:=FALSE; }ELSE {IF t.t ＞m[l].t { l:=i; }}}}
IF firing {
t:=m[l];
Fire the transition;
For each output places j of transitions k{
Broadcast for global detection or computer
spatial operator due to N[i,k];
FindAndFire(j);}}
其中SpatialOperate(mplace)为空间算子计算算法，输入为变迁位置，输出布尔型。对于二元SO，输入库所只保留最近的参考事件，如果变迁所有输入库所中的事件满足空间算子，则返回TRUE，否则返回FALSE。本文不详细列出。
2.3 应用实例
本实验过程包括：用户使用事件规范语言定义复合事件，经过复合事件编译器编译成功后存入数据库，并由CCPN构造器构造检测复合事件的组合着色Petri网存入数据库。当数据库内核中的原子事件检测器检测到原子事件发生后，通知CCPN检测器进行复合事件检测，检测结果通知应用程序，应用程序根据复合事件的发生调用ECA规则执行器执行下一步操作，用户也可以在应用程序中对数据库中的复合事件进行查询、更新等维护操作。图2为复合事件E4=OR(E1, NE(E2, E3))的全局模式检测实例。首先将该复合事件编译，然后构造CCPN，如图2(a)所示。最后进行复合事件检测。使用原子事件生成器按时间顺序产生事件类型为0～10的随机事件，事件的位置信息也是随机的，为了演示方便，将位置范围控制在地图可见区域。原子事件中构成复合事件的组件事件插入到组件事件列表中，每次插入则调用基于CCPN的复合事件检测器检测。由于采用Recent事件消耗策略，对于检测到的组件事件E2，如果多次出现，则只保留最近的，用于复合事件E4的检测。检测到NE(E2,E3)后，也消耗掉E2，E3，为了更清楚地演示，只在删除E2时置Eid为“D”标识。对于检测到的组件事件和复合事件的空间位置信息，在地图上进行了显示，图2(b)是针对实验数据的运行界面。
需要指出的是，实验假定时间轴等距离。实际情况中事件的发生并非按照等距离时间间隔" title="时间间隔">时间间隔，因此可以设定一个时间间隔阈值，根据事件发生的最小间隔来调整该阀值，这样就可以转换成等距离时间间隔的情况。另外实验中也没有考虑事件检测本身所要消耗的计算时间延迟。同时联接变迁和联接弧也可能在事件检测时间中造成一定的延迟。
针对现有的主动数据库事件检测机制难以满足空间事件检测的需求，本文建立了空间事件模型，在该模型基础上定义了基于空间关系的事件复合算子及其语义，并证明该定义对于复合运算是封闭的；为了简化构造复合事件检测Petri网，本文采用组合着色Petri网构造了复合事件检测模型，充分利用复合事件公共表达式，简化Petri网的构造；提出基于CCPN的检测算法；通过应用实例验证该检测模型是一个简洁、有效的复合事件检测机制。
本文没有考虑分布式环境下的空间事件检测机制，分布式环境下要考虑原子事件的并发性。全局模式下的事件采用链表简单结构管理，下一步将引入更好的数据结构以提高检测效率。同时空间算子的描述能力还不够强，不能满足更多用户的需求。将CCPN检测系统与空间数据库相结合，充分利用空间数据库的查询处理机制还需要做大量的工作。
参考文献
1 Xiaoyan Chen, Ying Chen,Fangyan Rao.An Efficient Spatial Publish/Subscribe System for Intelligent Location Based Services. San Diego USA： DEBS′03 2003
2 A. Hinze. Efficient filtering of composite events. In Proceed-ings of the BNCOD British National Conference on Datbases,London, UK, 2003
3 Jorn W. Janneck, Robert Esser, Higher-order Petri net modeling - techniques and applications Workshop on Software Engineering and Formal Methods, Adelaide, Australia：Petri Nets 2002
4 熊 伟，张 巨，景 宁.从空间完整性约束导出触发器ECA规则. 计算机科学，2003;30(10):207～209
5 左万利.复合时序事件及其基于Petri网的检测.系统工程学报，2003;18(3):262～267