一种用RBF神经网络改善传感器测量精度的新方法
2008-07-31
作者:赵望达 刘勇求 贺 毅
摘 要: 介绍一种利用径向基函数(RBF)神经网络和智能温度传感器DS18B20改善传感器精度的新方法。RBF网络具有良好的非线性映射能力、自学习和泛化能力,通过大量的样本数据训练构建了双输入单输出网络模型,采用改进的算法实现了传感器高精度温度补偿" title="温度补偿">温度补偿。
关键词: 传感器精度 温度补偿 径向基函数神经网络 温度传感器DS18B20
一般工业测控现场的环境温度变化急剧,传感器大多数都对温度有一定的敏感度,这样就会使传感器的零点和灵敏度发生变化,从而造成输出值随环境温度的变化而变化,导致测量出现附加误差,因此温度补偿问题一直是工业测控系统" title="测控系统">测控系统中的关键环节[1]。本文采用DS18B20智能温度传感器和RBF神经网络相结合的温度补偿新方法来实现传感器高精度温度补偿。本文介绍的方法将DS18B20测量值作为温度补偿输入,将传感器本身的测量值作为另一输入,用RBF神经网络构成双输入单输出的补偿模型,输出即为补偿后的测量值。RBF神经网络主要用于传感器的数据处理,以改善传感器测量精度。
1 DS18B20数字温度传感器测温" title="测温">测温原理
1.1 DS18B20的特性
DS18B20是美国DALLAS公司继DS1820之后推出的增强型单总线数字温度传感器,它在测温精度、转换时间、传输距离、分辨率等方面较DS1820有了很大的改进,这给用户带来了更方便的使用和更令人满意的效果。其特点如下:
(1)单线接口:仅需一根口线与单片机连接;
(2)由总线提供电源,也可用数据线供电,电压范围:3.0~5.5V;
(3)测温范围为:-55~+125℃,在-10~+85 ℃时,精度为0.5℃;
(4)可编程的分辨率为9~12位,对应的分辨率为0.5~0.0625℃;
(5)用户可编程的温度报警设置;
(6)12位分辨率时最多在750ms内把温度值转换为数字量。
1.2 DS1820引脚功能说明
DS1820的PR-35封装形式见图1,其外表看起来像三极管。另外还有8脚SOIC封装形式,只用3、4和5脚,其余为空脚或不需连接引脚。不过最常见的形式是PR-35封装,其引脚说明如表1所示。

1.3 DS1820温度数据格式
在DS1820中,转换温度值是以9位二进制形式表示的,而输出温度则是以16位符号扩展的二进制补码读数形式提供。采用的办法是将低八位用补码表示,第九位以符号扩展形式扩展至其它七位。具体温度表示格式见表2。
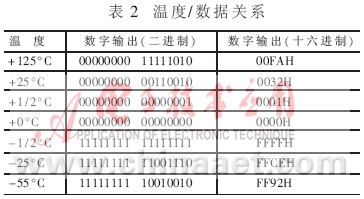
在实际应用中,测量温度往往在0°C以上,此时可只取16位二进制温度输出的低8位,即1个字节,这样将使计算和编程工作更为便利。
1.4 DS18B20的测温原理
DS18B20的测温原理为:内部计数器对一个受温度影响的振荡器的脉冲计数,低温时振荡器的脉冲可以通过门电路" title="门电路">门电路,而当到达某一设置高温时,振荡器的脉冲无法通过门电路。计数器设置为-55℃时的值,如果计数器到达0之前门电路未关闭,则温度寄存器的值将增加,这表示当前温度高于-55℃。同时,计数器复位在当前温度值上,电路对振荡器的温度系数进行补偿,计数器重新开始计数直到回零。如果门电路仍然未关闭,则重复以上过程。温度转换所需时间不超过750ms,得到的温度值的位数因分辨率不同而不同[2]。DS18B20同AT89C52单片机的接口电路如图2所示。这种接口方式只需占用单片机一根口线,与智能仪器或智能测控系统中的其它单片机或DSP的接口也可采用类似的方式。
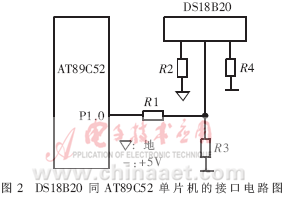
2 RBF神经网络及学习算法
RBF神经网络即径向基函数(Radial Basis Function)神经网络[3~4],其结构如图3所示。它很容易扩展到多输出节点的情形,在此只考虑一个输出变量Y的情况。RBFNN包括一个输入层、一个隐含层和一个输出层的最简模式。隐含层由一组径向基函数构成,与每个隐含层节点相关的参数向量为Ci(即中心)和σi(即宽度)。径向基函数有多种形式,一般取高斯函数[5]。具体如下:

上式中,m是隐含层结点数;||·||是欧几里德范数;X,Ci∈Rn, ωi是第i个基函数与输出结点的连接权值" title="权值">权值(i=1,2,...,m)。

RBF神经网络是一种性能良好的前向网络,它具有最佳逼近性能,在结构上具有输出—权值线性关系、训练方法快速易行、不存在局部最优问题的特点。该网络的学习算法有很多种,本文将带遗忘因子的梯度下降法应用于RBF神经网络的参数调整[6],即在考虑当前时刻(k时刻)的网络状态的变化时,将前一个时刻(k-1时刻)的网络参数变化也包括进去。其具体算法如下:

其中,J为误差函数,Y(k)代表希望的输出,Y(W,k)为网络的实际输出,W是网络的所有权值组成的向量。
隐层—输出层连接权值矩阵的调整算法为:

隐层中心值矩阵的调整算法为:

隐层标准偏差矩阵的调整算法为:
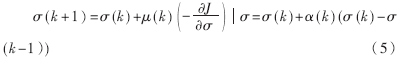
其中,μ(k)为学习率,α(k)为动量因子,也称为遗忘因子,又称动量项或阻尼项。将其称为遗忘因子可从对于新旧信息的学习与遗忘的角度来理解;称为动量项或阻尼项是因为在网络的学习训练中,此项相当于阻尼力,当训练误差迅速增大时,它使网络发散得越来越慢。总之,它使网络的变化趋于稳定,有利于网络的收敛。
3 测试方法及推广应用分析
实验中以测量压力为例,采用Honeywell的24PCGFA1G型压力传感器。将传感器测量值和DS18B20的输出值作为网络输入层节点的输入,与其对应的压力是网络输出层节点的输出。采用的RBF神经网络为三层网络结构,其中,输入层有2个节点,隐含层有8个节点,输出层有1个节点。基于上一节中提到的网络参数调整算法,通过调整RBF网络中的可调参数(隐层节点数、学习速率、遗忘因子和网络权值、隐层标准偏差等)进行网络的训练和测试,并采用均方根(RMS)计算其训练精度和测试精度。共采集样本数据120组,其中72组作为网络训练样本,48组作为网络测试样本,在环境温度变化范围为-5℃~75℃时,最佳RBF的神经网络的训练精度为0.048%,测试精度为0.062%。同时基于获得的实验数据,采用最小二乘拟合方法建立的数学模型,其拟合精度为0.170%;用单片机直接预存线性插值补偿的方法,测试精度为0.280%。
对于其它参数的检测,如流量、浓度或温度本身,也可采用增加温度或其它辅助传感器来实现补偿的方法。对于同时存在温、湿度漂移的测量场合,可以采用温湿度一体化传感器进行补偿。在本文图3所示的神经网络中增加一个X3输入代表湿度,只是会增加具体计算的复杂性。
DS18B20测温已普遍应用,且有着价格低廉、同基于单片机的智能仪器或测控系统接口简单的突出优点,本文将其引入作辅助测量传感器,在传感器温度补偿领域是一种有益的尝试。RBF网络是一种性能良好的前向网络,它不仅有全局逼近性质,而且具有最佳逼近性能。将带遗忘因子的梯度下降算法应用于RBF神经网络的参数调整,该算法具有良好的非线性映射能力、自学习和泛化能力,鲁棒性好、收敛较快,特别适用于传感器数学模型的建立。论文采用软硬件相结合的方法实现了高精度的温度补偿。与最小二乘拟合方法及线性插值补偿方法相比,其精度提高了2~5倍。
参考文献
1 樊尚春,彭春荣.硅压阻式传感器的温度特性及其补偿[J].微纳电子技术,2003(7):484~488
2 赵望达.DS18B20数字温度传感器在机械设备温度监测控制中的应用[J].制造业自动化,2001;23(5):52~54
3 Monica Bianchini. Learning without Local Minim in Radial Basis Function Networks[J]. IEEE Trans. On Neural Networks,1995;6(3):749~755
4 Yao Xin. Evolving Artificial Neural Networks[J]. Proceedings of the IEEE,1999;87(9):1432~1447
5 Catelsni M, Fort A. Fault Diagnosis of Electronic Analog Circuit Using a Radial Basis Function Network Classifier [J]. Measurement, 2002;28: 147~148
6 张广军,武晓利.基于RBF神经网络的红外二氧化碳传感器数学模型[J].仪器仪表学报,2004;25(1):72~75

