一种QCM信号在线采集系统的实现
2008-08-07
作者：王久才 蒋海峰 赵 松 潘
摘 要： 石英晶体" title="石英晶体">石英晶体微天平（QCM）信号采集系统的设计质量是影响其测量精度的重要因素。提出了一种QCM信号在线采集系统的实现方案，给出了系统的结构框图，并对系统电路进行了详细的分析。
关键词： 石英晶体微天平 DSP 谐振频率
QCM(Quartz Crystal Microbalance)是由AT切石英晶体片和镀在其上下表面的金属电极构成的一种谐振式传感器。其结构如图1所示。QCM作为微质量传感器具有结构简单" title="结构简单">结构简单、成本低、振动Q值大、灵敏度高、测量精度可以达到纳克量级的优点，被广泛应用于化学、物理、生物、医学和表面科学等领域中[1]，用以进行气体、液体的成分分析以及微质量的测量、薄膜厚度的检测等。根据需要，还可以在金属电极上有选择地镀膜，进一步拓宽其应用。例如，若在电极表面加一层具有选择性的吸附膜,可用来探测气体的化学成分或监测化学反应的进行情况[2]。若选用生物活性膜,则可制成生物传感器,如质量式的基因传感器等[3]。随着生物科学的蓬勃发展，QCM作为基因传感器在生物领域的应用有着广阔前景。
在国外，QCM在气相中的应用已经相当成熟，近几年，对液相中的QCM应用的研究也取得了很大进步，并且已经出现了很多商品化的产品，但是它们的价格非常昂贵。国内的相关研究相对较少。本文提出了一种基于DSP的QCM信号在线采集系统。该系统主要由高频信号发生器、QCM传感器和信号采集处理部分组成，结构简单、成本低。借助DSP强大的数字信号处理功能，实现了在线测量，并且保证了较高的测量精度。
1 QCM测量原理
石英是具有压电性质的物质之一，当外加交变电压的频率为某一特定频率时，石英晶片振幅会急剧增加,这就是压电谐振。
1959年Sauerbrey在假定外加质量均匀刚性地附着于QCM的金电极表面的条件下，得出了QCM的谐振频率" title="谐振频率">谐振频率变化与外加质量成正比的结论。即：
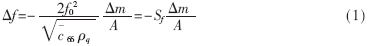
式中，Δf为QCM谐振频率的变化；f0为QCM的基频；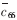
为石英的压电强化剪切模量；ρq为石英的密度：2.651g/cm3；A为金电极的面积；Sf为传感器的灵敏度；Δm为电极表面的质量变化。通过（1）式可得到QCM电极表面的质量变化。由于QCM的灵敏度很高，可以达到纳克级，并且结构简单，因此一问世就得到了广泛的应用，如用于真空或空气中膜的厚度检测等。
20世纪90年代以来，随着研究的深入，QCM在液相中也取得了广泛的应用，主要用于生物、化学等领域的检测中。1982年Monura和Okuhara最先提出了可以在液相中驱动QCM振动的电路，将QCM的应用扩大到了液相。1985年Kanazawa和Gordon推出了QCM在牛顿流体中振荡时其谐振频率变化与液体的粘度和密度的关系式[4]，即：
从式(1)、(2)可以看出，QCM谐振频率的变化量Δf是关键的待测量。
2 系统方案
目前驱动QCM振动并采集其输出信号的方法主要有两种：（1）振荡电路法；（2）频谱分析" title="频谱分析">频谱分析法。振荡电路法的基本原理为：将QCM接入自激振荡电路中，使其构成选频元件，电路的振荡频率等于QCM的谐振频率。通过电路振荡频率的变化可得到QCM谐振频率的变化，从而可推测出待测物质性质的变化。频谱分析法的基本原理为：扫描QCM在其谐振频率附近的一段频率范围内的频谱（幅频和相频特性），通过该频谱可得到QCM的谐振频率、Q值等参数。与振荡电路的方法相比，频谱分析的主要优点有：在大阻尼介质中不会停振、测量结果信息量大、形象直观、计算解释容易。本设计给出了一种基于频谱分析法的QCM信号采集系统，其电路原理框图如图2所示。
3 系统分析
电路的正弦信号产生部分由直接数字信号合成（DDS）芯片、自动增益控制（AGC）和运放（AMP）等组成。DDS接收DSP的控制信号，产生频率可控的正弦信号；AGC调整DDS的输出信号，使其峰-峰值始终保持为一个已知的定值；AMP则完成信号的放大和阻抗转换。由于信号产生部分增加了自动增益控制使其产生的信号的峰-峰值保持恒定，从而减少了待测信号的数目，简化了测量和处理的过程。
信号产生器部分产生的正弦信号作用在如图2中所示的两个反相" title="反相">反相比例电路上，反相比例电路的输出信号包含QCM在相应频率下的等效阻抗的幅值和相角信息。根据反相比例电路虚地的原理，作用在QCM上的电压始终保持为信号产生部分的输出电压与地之间的电压差。采用这种结构的好处是：（1）使作用在QCM上的电压保持恒定，简化了处理过程。（2）只通过一个反相比例电路的输出信号即可单独得到QCM等效阻抗的幅值（通过后面的计算将会得到此结论）。
反相比例电路输出信号的采集和处理部分的核心是两个乘法器和低通滤波器。设信号产生部分的输出信号电压为：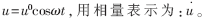
则含有QCM的反相比例电路的输出为：
式中，R1为参考电阻R1的阻值，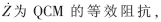
|Z|和φ为其对应的幅值和相角。另一个反相比例电路的输出为：
这两个直流信号经过放大器放大后由ADC芯片采集，所采集的数字信号经DSP处理后送往PC机供分析、显示之用。为保证采集的精度，此处的放大器选用AD620芯片。AD620具有高精度、低漂移和低噪声的优点,另外AD620可以通过一个外接电阻方便地调节放大倍数。ADC芯片采用双通道的高精度转换芯片。
整理（3）、（4）两式可得QCM等效阻抗的幅值为：
上面各式中R1、R2、R3和u0均为与电路参数有关的已知值,所以由采集的信号uf 1和uf 2，通过(5)、(6)式即可分别计算出QCM等效阻抗的幅值和相角。通过DDS改变产生信号的频率，即可得到不同频率下QCM等效阻抗的幅值和相角。对QCM谐振频率附件的频率段进行扫描，记录每个频率测量点对应的幅值和相角，即可绘出QCM的频谱。由频谱可以得出QCM谐振频率的变化量Δf。
由(5)式可知，通过uf1即可单独求出QCM等效阻抗的幅值，得到QCM的幅频特性曲线。因此本电路可以设定两种工作模式：(1)使电路仅采集信号uf1，从而得到QCM的幅频特性曲线，由该曲线可以得到QCM的谐振频率（对应于阻抗值最低点处的频率）、带宽、Q值等参数。采用此模式得到的信号虽不全面，但它足以得到谐振频率的变化量Δf，且由于这种模式只采集、处理一路信号，因此工作速度较快。(2)同时采集信号uf1和uf2，从而可得到QCM的幅频特性和相频特性曲线。采用此模式可以得到QCM的最全面的信息，但它的工作速度与模式(1)相比较慢。
数字信号的采集、处理、传输以及整个电路的控制是由DSP控制器、A/D转换芯片和PC机完成的。DSP的高速处理能力和较大的数据存储空间使得系统可以在线地采集处理信号。实际中，从低通滤波器输出的信号uf1、uf2是混杂着噪声的直流信号，为了消除引入的干扰信号，在DSP中采用滤波算法对数据进行滤波处理，可以进一步提高系统的精度。
本系统结构简单、成本低、易于实现。通过使作用在QCM上的信号峰-峰值保持恒定，简化了后续的计算处理过程。同时系统具有两种工作模式，可采集的信息量全面。系统的核心控制器由DSP担任，借助DSP强大的数字信号处理能力，可以实现信号在线采集，并对信号进行滤波处理，进一步提高了系统精度。
参考文献
1 朱则善. 石英晶体微天平(QCM) 及其在电化学研究中的应用[J].化学通报,1991(9):27～31
2 Antonio Arnau,Yolanda, Jimennez. An Ex2 tended Butterworth2Van Dyke Model for Quartz Crystal Microbalance Applications in Vis2 coelastic Fluid Media[J]. IEEE, 2001;48(5):1367～1381
3 刘建辉,莫志宏,刘明华. 基因传感器研究新进展[J].国外医学临床生物化学与检验学分册,2000;21(5):233～234
4 Keiji K.K., Gordon J.G. Frequency of a Quartz Microbalance in Contact with Liquid. Anal. Chem Acta,1985;59:99~104