EMT系统边界磁场检测线圈的动态补偿及图像重建
2008-08-20
作者:刘 泽 孙秀芳 熊汉亮
摘 要: 提出了一种应用于电磁层析" title="层析">层析成像(EMT)系统的磁检测线圈的动态补偿方法,实现了被测空间边界磁场检测的系统误差补偿。经过EMT系统的图像重建" title="图像重建">图像重建实验证明,这种补偿方法能够提高图像重建的精确性。
关键词: 电磁层析成像 工业CT 传感器 图像重建
电磁层析成像(Electromagnetic Tomography, EMT)技术是近十年来发展起来的一种新型过程层析成像技术[1]。它将电磁感应原理与“由投影重建图像”的理论相融合,通过检测被测空间边界的磁场信息重建空间中导电、导磁物质的时空分布图像,而且其传感器具有非介入、非接触和无危害的检测优点,因此可应用于工业过程中多相" title="多相">多相流检测[2]、化工分离、异物监测、地质勘探及生物电磁学研究[3]等领域。EMT系统图像重建质量的影响因素之一是其检测系统的准确性和测量的一致性。在检测系统的传感器设计中,检测边界磁场的多个检测线圈在工艺上难以做到完全一致,由此将直接导致重建图像的失真。为消除这种不一致性对图像重建造成的影响,作者设计了一种动态补偿算法,通过在多个激励方向下对检测线圈做综合补偿,提高了图像重建的精确性。
1 EMT系统结构及检测特点
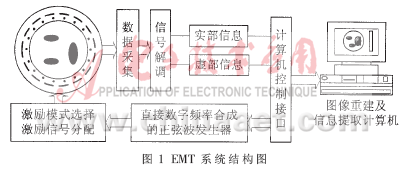
EMT系统的结构如图1所示。左边圆形结构为可安装于工业多相流管道的传感器截面。在被测管道的中心分布有多相流动物质,系统的检测目的是通过非接触、非介入的方式将管道内的不同物质的分布图像在计算机上得以重建,进而分析出多相流体的各种特征参数,并应用于测控系统中。为实现这一目的,由计算机控制图1所示的激励模式选择和激励信号分配系统,由激励系统在被测管道中激发出特定的激励场;然后与医学CT类似,使激励场在空间连续旋转,旋转的同时检测边界磁场的畸变情况,并由数据采集与处理系统实现磁场信号的解调;最后应用图像重建算法重建出被测空间的物质分布。
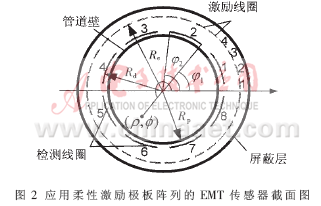
作者用柔性激励极板" title="极板">极板阵列实现的EMT传感器[4]的截面如图2所示。传感器由内到外依次是管道壁、检测线圈、激励层和屏蔽层。其中,检测线圈由8个沿管道外壁等距离分布的精密绕组构成,完成边界磁场的测量;激励层由柔性激励极板阵列构成;电磁屏蔽层由铁氧体和波莫合金构成。数据采集与信号处理电路实现各个激励角度条件下的边界磁场测量,激励和检测由图像重建计算机协调控制,同时该计算机完成图像重建和多相流特征参数的提取。激励极板阵列由32个均匀分布的柔性极板构成,通过改变极板的电流分布可实现不同的激励方式。其中,管道半径Rp=35mm,检测线圈半径Rd=38.42mm,激励线圈半径Re=55mm,磁屏蔽层内半径Rsin=60mm,被测管道直径为70mm。
对于这一传感器结构,需要补偿的就是检测层的8个检测线圈特性的一致性。但检测线圈的特性会受到线圈几何尺寸、安装角度、前端检测电路特性不一致的影响,而且线圈检测的信号是交变的磁场信号,其相位随激励方向的变化而改变,这些因素给检测线圈特性的补偿带来了困难。
2 检测线圈特性不对称的补偿
实现检测线圈特性不对称补偿的难点是检测信号是频率为187.5kHz的交流信号,而且各检测线圈输出的检测信号与激励基准信号之间有不同的相位差,这个相差会随检测角度的改变而变化。为此作者设计了一种补偿方法,其思路是使每个检测线圈在全部激励旋转方向下测量同一被测场,计算综合测量值并将其作为补偿系数,而补偿过程的实现则通过计算机控制激励场的旋转并对边界磁场进行连续检测来完成。在EMT系统进行图像重建时,首先选择空场作为检测线圈特性检测的参照场,来进行检测线圈特性测量;然后由公式计算出各检测线圈的补偿因子。采集进行图像重建的物场信号时,应用计算得到的补偿因子对测量数据进行修正。
对任意一个检测线圈检测补偿数据时,应分别测量其在所有激励场投影方向下的检测值。检测值包括通过解调电路得到的实部" title="实部">实部和虚部数据,所有激励方向下的检测值一起构成计算检测线圈特性补偿因子的参考矩阵。对于N个检测线圈,P个激励磁场旋转方向的EMT系统激励场需要旋转P次来获得全部N个检测线圈的补偿值,所以补偿参考矩阵由N行P列构成,其中每个元素都是检测线圈检测值的复数表示形式。本文介绍的EMT传感器系统中,N=8, P=16。
对于N个检测线圈,定义其特性补偿因子为K(i),其中i=1,2,.....N,表示检测线圈序号。K(i)可按照如下公式计算:
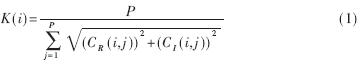
式中,j=1,2,…P,表示激励场投影方向序号;CR、CI分别为空场时在第j个激励方向下第i个检测线圈检测值的实部和虚部。
进行实际测量时,将每个检测线圈在各个激励方向下的检测信号的实部MR(i,j)和虚部MI(i,j)都乘以补偿因子K(i),从而得到各个检测线圈经过补偿后检测值的实部和虚部。

式中,ER(i,j)和EI(i,j)为经过补偿后的检测结果。
3 EMT检测线圈补偿前后的实验数据分析
为分析EMT传感器检测线圈进行特性补偿前后的测量数据,对传感器在同一种检测条件下各个投影方向、不同检测线圈的测量值进行分析,来比较补偿前后数据的分布特点。对于本实验的传感器系统,激励投影方向为16个,检测线圈为8个,所以共有128组测量值,其中每个测量值都包含实部和虚部。实验过程中为使每一个测量点的数据可靠,对数据进行多次检测并求取平均值,16个激励方向下8个检测线圈在128个测量点的测量数据如图3所示。图中所示的数据为每个测量点检测信号的模值,测量时被测空间为空场条件。

图3中(a)为未经补偿的检测数据M的图示,(b)为经过补偿计算后的检测数据E的图示。图中底部平面为测量点的图示,上部为各个测量点检测信号模值的图示,其中,N轴为检测线圈序号轴,P轴为激励投影方向序号轴,M轴和E轴为检测信号的模值。由图3(b)可知,对于一个固定的激励投影方向,各个检测线圈的检测值符合正弦规律;对于某一检测线圈,当激励场沿圆周旋转时,其检测值的模值也呈正弦分布。图3(a)中各个检测线圈在16个激励方向下的分布幅度不同,这体现出各线圈检测特性的不一致,但在图3(b)中,这一现象得以补偿。所以由补偿前后的数据图示可以看出,这种检测线圈特性补偿算法在不改变检测数据随投影方向的分布结构的前提下,使得在同一种激励场下各线圈的检测特性趋于一致。
4 补偿方法在EMT系统中的实现
这种补偿方法在实验系统中的实现可通过软件控制自动完成。每次实验系统启动时,首先进行补偿因子的计算,获得补偿因子后在实际物场测量时将检测线圈的检测值按照补偿算法进行修正。由补偿因子的计算方法可知,为实现补偿因子的计算,需要在EMT系统启动时保持被测空间为空场,这样每次得到的补偿值就是符合当时检测环境条件的补偿值。如果在系统启动时不能满足空场条件,则需要屏蔽这一自动补偿功能,补偿时可使用预先测得并存储起来的补偿因子。
应用该补偿算法进行图像重建的实验结果如图4所示。图像重建的实验条件是:被测物体为直径15mm的铜棒,放置于传感器的中央,激励场激励频率为187.5kHz。图中的中间部分表示被测物质在传感器截面上分布的概率。

图4中左边的重建图像是检测线圈未经补偿获得的结果,右边的重建图像为每个检测线圈按照本文所述方法进行补偿后获得的结果。为显示重建图像的全部信息,没有对概率阈值以下的点进行截断滤除。由两图像比较可知,补偿后的图像较准确地反映了被测铜棒的分布位置,同时也说明EMT图像重建对检测数据的变化非常敏感,检测线圈特性不一致产生的微小误差就可以造成重建图像的较大偏移。
参考文献
1 Yu Z Z, Peyton A J, Xu L A,Beck MS. Electromagnetic Inductance Tomography (EMT): Sensor, Electronics and Image Reconstruction Algorithm for a System with a Rotatable Parallel Excitation Field. IEE Proceedings:Science,Measurement and Technology ,1998;145(1):20~25
2 Ramli S, Peyton A J. Feasibility Study of Planar-Array Electromagnetic Inductance Tomography (EMT). 1st World Congress on Industrial Process Tomography, Buxton, Greater Manchester, April 14-17, 1999 :502~510
3 Griffiths, H. Magnetic Induction Tomography. Measurement Science and Technology, 2001;12(8):1126~1131
4 刘 泽, 何 敏, 徐苓安等.多激励模式的电磁层析成像系统. 仪器仪表学报,2001(6):614~617EI:02106877824

