在通信系统中,由于信道存在大量的噪声和干扰,使得经信道传输后的接收码与发送码之间存在差异,出现误码。在数字通信系统中常采用差错控制信道编码技术,以此来减少传输过程的误码,提高数字通信系统的传输质量。它的基本原理是:发送端的信道编码器在信息码元序列中按照一定的关系加入一些冗余码元(称为监督码元),使得原来相关性很小的信息码元产生某种相关性,从而在接收端利用这种相关性来检查并纠正信息码元在传输中引起的差错。冗余度的引入提高了传输的可靠性,但降低了传输效率。
1 线性分组码
分组码是由一组固定长度为n,称之为码字的矢量构成的。线性分组编码时,将每k个信息位分为一组独立处理,按一定规则给每个信息组增加(n-k)个监督码元,组成长度为n的二进制码字,这种编码方式记为是(n,k)分组码。信息位和监督位采用的关系式由一组线性方程所决定,称之为线性分组码。
若线性分组码的输入信息位为U=(U0,U1,…,Uk),编码输出为C=(C0,C1,…,Cn),则有如下关系:

式中:G为线性分组码的生成矩阵;H为监督矩阵。当G确定后,编码的方法就完全确定了,而H给定后,编码时监督位和信息位的关系也就确定了。因此,在设计分组码编码器时,需要确定生成矩阵G;在设计分组码译码器时,需要确定监督矩阵H。
2 线性分组码编译码器设计
2.1 线性分组码编码器设计
设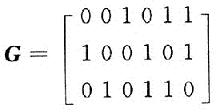 ,由于生成矩阵G是k行n列,所以k=3,n=6,改(n,k)码为(6,3)码。根据生成矩阵和式(1)运算后得到相应的编码。即由:
,由于生成矩阵G是k行n列,所以k=3,n=6,改(n,k)码为(6,3)码。根据生成矩阵和式(1)运算后得到相应的编码。即由:
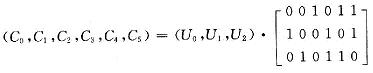
可得:
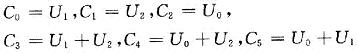
COUT=(C0,C1,C2,C3,C4,C5)为编码输出,其中前3个分量为增加的监督码元,后3个为原输入信息位。
2.2 线性分组码译码器设计
将生成矩阵G进行初等运算:原矩阵的第2,3,1行分别作为典型矩阵的第1,2,3行,可得典型生成矩阵:
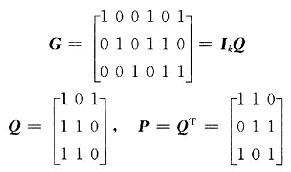
于是,典型监督矩阵H为:
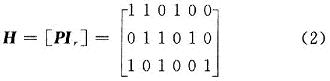
监督码元与信息码元之间的关系称为监督方程式(监督关系式),监督矩阵的每行中“1”的位置表示相应码元之间存在的监督关系,即下述三个监督方程:
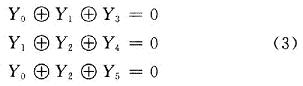
发送的码字C=(C0,C1,…,Cn)。e表示传输中的差错;Y表示接收的码字。如果码字在传输过程中没有出现差错,则有![]() HYT=HeT=O;出现差错时,则有,S=eHT。其中,S称为伴随子,又称为校正子。由于S只与序列传输中的差错e有关,因此在编码的能力之内,一定的e序列必然对应一定的S组合。可以在接收机中做好对应表,然后根据序列S准确地判断差错位置,再根据出错位置进行纠正,可得到正确的译码输出。根据式(2)可计算接收矢量Y的伴随子S=Y·HT。这里:
HYT=HeT=O;出现差错时,则有,S=eHT。其中,S称为伴随子,又称为校正子。由于S只与序列传输中的差错e有关,因此在编码的能力之内,一定的e序列必然对应一定的S组合。可以在接收机中做好对应表,然后根据序列S准确地判断差错位置,再根据出错位置进行纠正,可得到正确的译码输出。根据式(2)可计算接收矢量Y的伴随子S=Y·HT。这里:
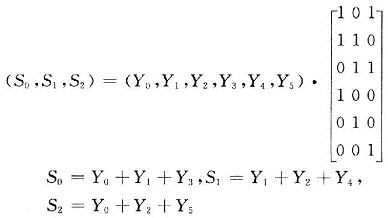
错误图样即校正子与错码位置的关系,因为r=3,所以有3个校正子,相应的有3个监督关系式。将式(3)改写为:
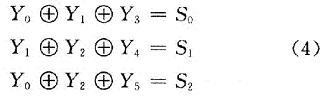
则可得由伴随子S决定对应的错误图样集e,即为典型监督矩阵的转置HT,如表1所示。
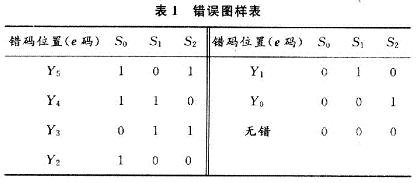
3 仿真及分析
图1、图2分别为线性仿真分组编码器、译码器电路的仿真波形。图中各参数含义如下:clk是系统时钟信号输入;UI是编码器中三位线性分组码的输入;CO是编码器中六位编码的输出;Y是解码器中六位编码的输入;c是解码器中六位译码的输出。
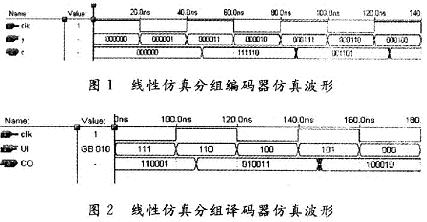
在图1、图2中,截取了仿真的部分波形进行分析,产生的六位编码CO、六位译码Y完全依据线性分组码的编译码规则,任意两个许用码组之和(逐位模2加)仍为一许用码组,即具有封闭性。
4 结语
对线性分组码编、译码器的设计基于VHDL(硬件描述语言),与传统设计相比较,采用VHDL语言设计的线性分组码编、译码器无需考虑具体电路的实现,只需要掌握编译码原理,根据相应的编译码规则转换成VHDL语言,大大减少了设计人员的工作量,提高了设计的准确性和效率。程序已在Max+PlusⅡ10.O工具软件上进行了编译、仿真和调试。经过实验结果的分析,说明本设计是正确的。本文给出的设计思想也适用于其他基于PLD芯片的系统设计。

