自适应算术编码的FPGA实现
2008-08-22
作者:姜勤忠 李建华 马幼军 林
摘 要: 在简单介绍算术编码" title="算术编码">算术编码和自适应算术编码的基础上,介绍了利用FPGA器件并通过VHDL语言描述实现自适应算术编码的过程。整个编码系统在ALTERA公司的MAX+plusⅡ软件上进行了编译仿真,测试结果表明:编码器各个模块的设计在速度和资源利用两方面均达到了较优的状态,可以满足实时编码的要求。
关键词: 算术编码 自适应 FPGA VHDL 仿真
算术编码是一种无失真的编码方法,能有效地压缩信源冗余度,属于熵编码的一种。算术编码的一个重要特点就是可以按分数比特逼近信源熵,突破了Haffman编码每个符号只能按整数个比特逼近信源熵的限制。对信源进行算术编码,往往需要两个过程,第一个" title="第一个">第一个过程是建立信源概率表,第二个过程是对信源发出的符号序列进行扫描编码。而自适应算术编码在对符号序列进行扫描的过程中,可一次完成上述两个过程,即根据恰当的概率估计模型和当前符号序列中各符号出现的频率,自适应地调整各符号的概率估计值,同时完成编码。尽管从编码效率上看不如已知概率表的情况,但正是由于自适应算术编码具有实时性好、灵活性高、适应性强等特点,在图像压缩、视频图像编码等领域都得到了广泛的应用。
现场可编程门阵列(FPGA)是一种新兴的可编程逻辑器件,具有更高的密度、更快的工作速度和更大的编程灵活性,被广泛应用于各种电子类产品中。而硬件描述语言(HDL)是一种快速的电路设计工具,其功能涵盖了电路描述、电路合成、电路仿真等的三大电路设计工作。VHDL是HDL的一种,因其简单易懂而被广泛使用。本文采用VHDL编程实现了自适应算术编码,为算术编码器的硬件实现提供了借鉴。
1 算术编码的基本原理[1]
实现算术编码首先需要知道信源发出每个符号的概率大小,然后再扫描符号序列,依次分割相应的区间,最终得到符号序列所对应的码字。整个编码需要两个过程,即概率模型建立过程和扫描编码过程。
算术编码的基本原理是:根据信源可能发出的不同符号序列的概率,把[0,1]区间划分为互不重叠的子区间,子区间的宽度恰好是各符号序列的概率。这样,信源发出的不同符号序列将与各子区间一一对应,因此每个子区间内的任意一个实数都可以用来表示对应的符号序列,这个数就是该符号序列所对应的码字。显然,一串符号序列发生的概率越大,对应的子区间就越宽,要表达它所用的比特数就越少,因而相应的码字就越短。
图1给出一个实现算术编码的示例。要编码的是一个来自四符号信源{A, B, C, D}的由五个符号组成的符号序列:ABBCD。假设已知各信源符号的概率分别为:P(A)=0.2,P(B)=0.4,P(C)=0.2,P(D)=0.2。编码时,首先根据各个信源符号的概率将区间[0,1]分成四个子区间。符号A对应[0,0.2],符号B对应[0.2,0.6],符号C对应[0.6,0.8],符号D对应[0.8,1.0]。符号序列中第一个符号是A,其对应的区间为[0,0.2],接下来将这个区间扩展为整个高度,再根据各个信源符号的概率将这个新区间分成四段;第二个符号是B,它对应新的子区间的第二个子区间,即对应区间[0.04,0.12];再将该区间扩展为整个高度,再根据各个信源符号的概率将这个新区间分成四段。继续这个过程直到最后一个符号得到一个区间[0.08032,0.0816],这样该区间内的任何一个实数就可以表示整个符号序列,如0.081。

2 自适应算术编码的基本原理
自适应算术编码在一次扫描中可完成两个过程,即概率模型建立过程和扫描编码过程。
自适应算术编码在扫描符号序列前并不知道各符号的统计概率,这时假定每个符号的概率相等,并平均分配区间[0,1]。然后在扫描符号序列的过程中不断调整各个符号的概率。同样假定要编码的是一个来自四符号信源{A, B, C, D}的由五个符号组成的符号序列:ABBCD。编码开始前首先将区间[0,1]等分为四个子区间,分别对应A,B,C,D四个符号。扫描符号序列,第一个符号是A,对应区间为[0,0.25],然后改变各个符号的统计概率,符号A的概率为2/5,符号B的概率为1/5,符号C的概率为1/5,符号D的概率为1/5,再将区间[0,0.25]等分为五份,A占两份,其余各占一份。接下来对第二个符号B进行编码,对应的区间为[0.1,0.15],再重复前面的" title="面的">面的概率调整和区间划分过程。具体的概率调整见表1。
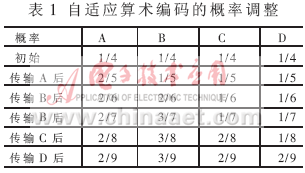
随着符号序列中符号个数的不断增多,由自适应算术编码器估计得到的各符号的概率将趋于各符号的真实概率。
3 自适应算术编码的FPGA实现[2]
3.1 总体设计
在利用FPGA实现自适应算术编码的过程中,首先遇到的问题就是将浮点运算转化为定点运算,即将[0,1]区间的一个小数映射为一个便于硬件实现的定点数。考虑到硬件实现的简便性,本文中将[0,1]之间的浮点数与[0,256]之间的定点数对应。相应的对应关系如表2所示。

编码器在实现编码的整个过程中按照耦合弱、聚合强的原则分为四个模块:修改码表、计算确定区间、并行编码" title="并行编码">并行编码、串行输出。四个模块相对独立,通过输入、输出信号使其构成一个整体。系统的顶层结构如图2所示。
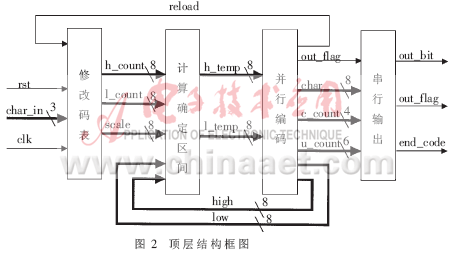
3.2 码表的设计及修改
自适应算术编码器可以在许多场合中得到应用。本文实现的自适应算术编码器应用在采用6符号对小波变换系数进行零树编码的小波域视频编码中[3],因此设计的码表中含有六个符号。这样根据自适应算术编码的基本原理,将区间分成六个子区间,整个区间含有七个分割点。所以码表可以用七个8位寄存器表示。初始时设定为等概率,这时七个寄存器可以顺序地存储0到6这七个数,即每个子区间的数值为1。随着符号不断地输入,自适应地修改码表,并且在修改码表的过程中时刻要保持寄存器中的数值是递增的。
修改码表时,首先判断输入符号,确定其所在区间,同时为后续模块输出该子区间的两个端点值l_count和h_count以及码表的最后一个端点值scale,然后进行码表的修改:将当前符号所在区间之后的所有端点值都加1,即当前区间及后面所有子区间的h_count=h_count+1,这样即完成了码表的修改。在数值不断累加过程中,寄存器中存储的值将不断增大。当码表中最后一个寄存器中的数值为255时,需要对每一个寄存器中的值都取半,并同时对相邻的两个寄存器中的值进行比较,时刻保持数值是递增的。这样,处理前后的概率十分接近,对压缩比影响不大。
修改码表模块在输出h_count、l_count和scale之后,后面的计算子区间的模块即可进行计算;而修改码表模块在输出h_count、l_count和scale之后,亦可进行码表的修改。因此,这两个操作可以采用并行处理的方法实现,极大地节省了所用的时钟周期,相应地提高了速度,达到了优化的目的。表3给出了输入符号为3(对应于寄存器2与寄存器3之间的区间)时码表的修改过程。

3.3 区间计算及确定
初始时符号所在的总区间为high=0xff,low=0(high和low分别表示已编码的符号序列所在子区间的上下界)。随着符号的不断输入,high和low的值也不断地减小,用以表示输入符号序列所对应的子区间。通过如下的公式可确定输入符号的区间:
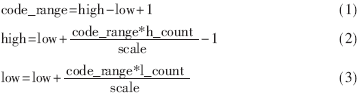
计算时,最耗资源的是乘法器和除法器。本方案中乘法器采用参数化模块lpm中的lpm_mult生成,而除法器则自行编写。虽然占用的时钟周期较多,但与使用lpm相比,这样做可以大大地提高工作频率,从总体上提高性能。
3.4 并行编码
在区间计算过程中,high和low总是有限值,不可能无限制地划分下去。为了能够实现连续的编码,通过对high和low的处理,可以实现利用有限长的寄存器表示无限精度的区间,即在不断修改high和low的过程中输出high和low中相同的高端位,形成输出码流。详细过程如下:
在区间确定之后,将low和high按位比较,若首位" title="首位">首位相同,则输出首位二进制码,产生输出码流,同时把low和high左移,low末位补0,high末位补1。循环比较输出,直到首位不同为止。如:
high = 00110110
low = 00100111
输出码流为001,而high和low的结果为:
high = 10110111
low = 00111000
通过这种连续地处理便可生成符号序列的自适应算术编码结果。但随着待编码符号序列的不断输入,可能会出现high和low十分接近,并且high和low的首位没有相同位的情况,如:
high = 10000000
low = 01111111
称这种现象为产生了下溢。产生下溢后,后面的编码都失去了意义,此时需要特殊处理。
对于下溢的处理方法为:保留首位,同时删除紧接在首位后的high中连续的0和low中连续的1,并且保证对high和low删除的位数相同,若连续0和连续1的位数不同,则取其较小者;然后把high和low左移相同的位数,同时high的低位补1,low的低位补0。表4给出了下溢处理前后high和low值。

经过处理后,扩大了区间,使得后面的编码可以顺利地进行。
在考虑了下溢的编码输出中,下溢作为输出码流的一部分,使得解码时能对下溢进行同样的处理,达到编解码的一致。但是下溢产生后并不马上输出,只记下下溢的个数,下溢则是在下一个符号编码时进行输出的。在下一个符号编码时,如果high和low比较后高端有相同位则输出下溢,即在第一个输出位后紧接着插入首位的反,插入首位反的个数为前面产生下溢的个数,然后输出相同的次高位及以后相同的各位。这样处理既保留了下溢的信息又使得输出码流不偏离编码符号所在的子区间,使得解码时很容易处理。但是如果high和low比较后没有相同位输出则不输出下溢,而是把两次产生的下溢的个数进行累加,再输入下一个符号,直到high和low有相同首位才输出下溢。
例如:在一个符号编码计算后得到的high=11010010和low=11001101,而前一个符号编码产生的下溢为1个,比较后输出为1010,同时记录下产生的下溢2个,如表5所示。

3.5 串行输出
并行编码后产生的码流存储在并行数据中,但在大多的情况下只有两、三个输出,甚至没有输出,若采用并行输出,就会产生极大的浪费。为了充分利用资源,在并行编码之后进行并/串转换,使其一位一位地输出,并且这个输出过程与下一个符号编码的过程并行完成,因此并不占用多余的时钟周期。
在编码过程中,当一个符号编码结束后,触发reload信号,通知此次编码结束,进行下一次编码,读取输入的符号。同时需判断输入是否合法,如果是合法的输入,就进行编码;否则停止编码,处于等待状态,直到复位信号rst置1,重新初始化、编码。
4 仿真结果
本文算法采用VHDL硬件描述语言实现,并在ALTERA公司的MAX+plusⅡ软件上编译仿真。设计采用全局同步时钟,避免了毛刺的产生,保证了信号的稳定性。编码的仿真结果如图3所示。
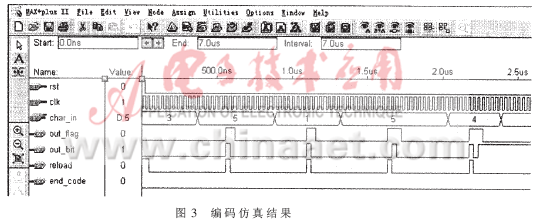
其中,rst、clk、c为输入信号,rst为模块中各寄存器的初始化信号,clk为时钟同步信号,而c则为输入的编码信号;out_flag、out_bit、reload、end_code为输出信号,out_flag和out_bit分别为输出标志位和输出位(若out_falg=1,则此时out_bit为有效输出;否则out_bit输出无效),reload为一个符号编码结束)下一个符号输入的标志位,end_code为编码结束的标志(若end_code=0,则继续编码,否则编码结束)。
在进行性能仿真时[4],采用的器件是FLEX1K系列的EP1K30TC144-1器件,其最大工作频率为40MHz,消耗1533个LC,平均编码时间为20个时钟周期。一个符号的编码时间不到500ns,对于QCIF格式的图像完全可以满足每秒钟实时编码30帧图像的要求。
自适应算术编码是一种效率很高的无失真编码,本文通过VHDL语言实现了自适应的算术编码,在编码过程中,根据硬件结构的特点,充分利用其并行特性。通过并行执行,实现了速度的优化。由于满足每秒钟编码30帧图像的要求,因此可以应用于视频图像的实时编码中。
参考文献
1 Mark Nelson. Arithmetic Coding + Statistical Modeling = Data Compression.Dr.Dobb’s Journal,February 1991
2 Uwe Meyer-baese著,刘 凌,胡永生译. 数字信号处理的FPGA实现. 北京:清华大学出版社, 2003
3 Arturo San Emeterio Campos. http://www.arturocampos.com/ac_arithmetic.html, 1999
4 潘 松,黄继业.EDA技术实用教程.北京:科学出版社,2002

