基于脉冲同步的混沌保密通信系统
2008-08-26
作者:金 虎, 王可人
摘 要: 介绍了脉冲混沌同步" title="混沌同步">混沌同步的基本原理,提出了基于脉冲同步的一般化混沌保密通信系统" title="通信系统">通信系统。针对该系统存在的传输时间帧拥堵问题,提出一种“信息感应”脉冲同步系统。该系统中有用信息被嵌入在发射端的同步脉冲" title="同步脉冲">同步脉冲里,在接收端" title="接收端">接收端再通过这些脉冲被感应出来,解决了时间帧拥堵的问题。
关键词: 脉冲同步 混沌保密通信 时间帧拥堵
1990年,美国海军实验室研究人员Pecora和Carroll首次利用驱动—响应法实现了两个混沌的同步后,混沌同步技术和混沌保密通信成为国际、国内通信领域的一个研究热点。国际上相继提出了各种混沌通信制式及其理论与方法,由此使混沌保密通信成为现代通信领域的一个新的分支。
混沌保密通信发展历经了四代[1]。第一代为1993年提出的加性混沌遮掩系统和混沌键控系统;第二代为1993~1995年提出的混沌调制系统;第三代为1997年提出的混沌密码系统;第四代为1997年提出的基于脉冲控制理论的脉冲同步混沌系统" title="混沌系统">混沌系统。
混沌同步是建立一个混沌保密通信系统的关键技术。实际上,正是混沌同步的发展引起混沌保密通信系统的发展。第一代混沌保密通信基于最简单的混沌同步,立足于反馈控制理论。第二、三代混沌保密通信基于自适应同步,源于自适应控制理论。大体上,前三代的混沌同步均为连续同步。前三代的不足之处在于同步信号的带宽相对于发送的信息较宽,需要30kHz,信道利用率低。基于脉冲同步的第四代混沌保密通信系统可以克服这个不足,一个三阶混沌发射机的同步信号只需不大于94Hz的带宽。
另外,现在的一些混沌保密通信系统均基于低维的混沌系统,这样的低维系统未必足够安全。出于安全考虑,一种方法是开发高维超混沌(至少两个正李雅普诺夫指数)保密通信系统,但是这样的系统同步更困难;另一种方法就是将传统的密码学方法与混沌系统结合以提高低维混沌保密通信系统的安全性。要克服低维连续混沌系统的低安全性,有两个途径:一是使发射的信号更加复杂,二是减少发射信号中的冗余信息。文献[3]提供了一个传统的密码学方法与低维混沌信号结合产生极其复杂的发射信号的例子。脉冲同步提供了一种较理想的减少发射信号中冗余信息的方法。由于只有同步脉冲送到响应系统,传输信号的冗余信息减少,从这个意义上说,即使低维的混沌系统也能提供较高的安全性。
1 脉冲同步原理[1,7]
令x=(x1,x2,…,xn)′,在脉冲混沌同步系统中,驱动系统为如下的非线性系统
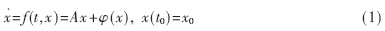
其中,φ(x)为非线性项。响应系统为

在离散时刻τi,i=1,2…,驱动系统的状态变量发送到响应系统,使得响应系统的状态变量在这些时刻发生跳变。用脉冲微分方程描述响应系统为:

当脉冲间隔较小时,脉冲同步混沌系统对信道加性噪声和参数失配都比连续同步混沌系统具有更好的鲁棒性[1,2,4]。但是脉冲同步与其他的连续同步方法相比,同步建立时间比较长[6]。
2 一般化的脉冲同步混沌保密通信系统
许多文献[1~2]提到的基于脉冲同步的混沌保密通信系统的框图如图1所示。该系统将脉冲同步与传统的密码学技术相结合,达到了既增加发射信号的复杂度又减少发射信号的冗余信息的目的。它由一个发射机和一个接收机组成,在发射端和接收端都包含一个同样的混沌系统。
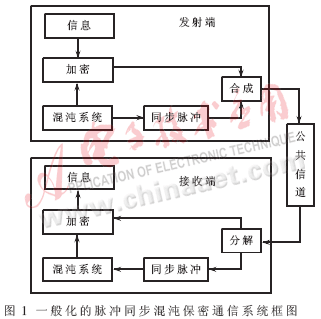
发射到公共信道的信号由一系列时间帧组成。每一帧持续时间为T秒,由两个区域组成:第一个区域是由同步脉冲组成的同步区,用于同步混沌保密通信系统的发射端和接收端,持续时间Q秒;第二个区域是加密后的信息区,包含加密后的信息,持续时间为T-Q秒。为了确保同步,一般要求T<△max,△max为同步脉冲间隔的上限。发射端的合成模块将同步脉冲信号和加密后的信息合成为一个时间帧。最简单的合成方法是将每一帧的前Q秒发送同步脉冲信号,后T-Q秒发送加密后的信息。接收端的分解模块将每一时间帧的同步区域与加密后的信息区域分开,分离出的同步脉冲用于同步接收端和发射端的混沌系统,产生密钥信号。密钥信号和被加密的信息送到解密模块,恢复出所需的信息。
影响系统脉冲同步性能的主要因素有两个:一是为达到同步的最小脉冲宽度Q,另一个是时间帧的长度T。(脉冲周期)以蔡氏振荡电路做实验,可以得到在不同的脉冲周期T时为达到同步的最小脉冲宽度Q及Q/T,结论如下[2]:
·当T<9.0×10-6s时,脉冲宽度仅需脉冲周期的8%即可达到“几乎一样”的同步,剩下92%的时隙可以用来传输加密后的信息。在这种情况下,Q随着T同比例变化,即Q/T的值固定。此时,可认为相对于T而言Q充分地小,传输加密信息时损失时间可以忽略不计。
·当9.0×10-6s<T<5.0×10-5s时,随着T的增加,Q/T的值从8%增加到50%,用于传输加密后的信息的时隙就相应减小了。
·当5.0×10-5s<T<5.0×10-3s时,为了达到“几乎一样”的同步,脉冲宽度至少占据脉冲周期的50%。相对T而言,Q完全不能被忽略。
整个系统的安全性依赖于发射端和接收端的混沌系统的参数和结构。在军事上,可以通过插拔不同的“硬件密钥”(混沌电路)达到极高的保密目的。对于商业移动通信,每个移动站的混沌系统结构将保持一致,但是不同的移动站可以设定不同的参数以提高保密性。
3 一种改进的脉冲同步混沌保密通信系统
上述的脉冲同步系统可以达到发射信号的复杂性和低冗余性这两个较理想的特性,而且有着较高的带宽利用率,但是这种脉冲同步系统会出现传输时间帧拥堵的问题。上一节已提到,同步的精确度既取决于时间帧的长度T也取决于脉冲的宽度Q。当脉冲周期增加时,同步脉冲的最小宽度也会随着增加,这就意味着当时间帧的长度大于某一限度时,脉冲宽度Q就会占据整个时间帧T,时间Q将完全不能被忽略,这将导致时间帧拥堵。当采用超混沌系统时,这种情况会更严重。在超混沌系统中,需要两个同步脉冲区(每一个区都为Q秒),为了达到“几乎一样”的同步,当1.3×10-5s<T<2.0×10-5s时,2Q/T达到了100%[2],没有时隙可以用来传输加密后的信息了。下面介绍的脉冲同步系统可以很好地解决时间帧拥堵的问题[5]。
该脉冲同步系统运用一致同等有界性和同等拉格朗日稳定性理论,通过脉冲控制一个非自治的两阶系统同步收发端。在该系统中,密钥信号(混沌信号)和加密后的信息都没有发送到公共信道,它们被嵌入在同步脉冲里,在接收端通过这些脉冲被“感应”出来。因此,这种系统被称为“信息感应”脉冲同步混沌保密通信系统,框图如图2所示。
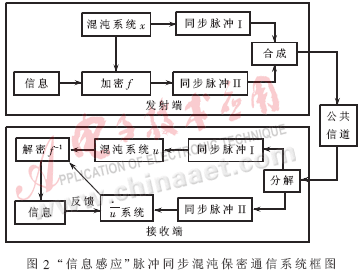
该系统由一台发射机、一台接收机和一公共信道组成。发射端和接收端分别包含一个混沌系统x和u,用来产生密钥信号并驱动它们各自在发射端和接收端的微分系统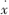 和
和 ,在发射端,系统
,在发射端,系统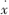 作为加密模块对需发送的信息进行加密。发射端和接收端各有两个同步脉冲模块,同步脉冲Ⅰ用于同步x和u,同步脉冲Ⅱ用于同步
作为加密模块对需发送的信息进行加密。发射端和接收端各有两个同步脉冲模块,同步脉冲Ⅰ用于同步x和u,同步脉冲Ⅱ用于同步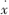 和
和 。发射端的合成模块将两个同步脉冲模块的同步脉冲组合成长度为2Q的时间帧,前Q秒是同步脉冲Ⅰ,后Q秒是同步脉冲Ⅱ。时间帧通过公共信道传输到接收端的分解模块。分解模块将时间帧分解为两个Q秒,前Q秒信号送到系统u,恢复出密钥信号,后Q秒信号送到系统
。发射端的合成模块将两个同步脉冲模块的同步脉冲组合成长度为2Q的时间帧,前Q秒是同步脉冲Ⅰ,后Q秒是同步脉冲Ⅱ。时间帧通过公共信道传输到接收端的分解模块。分解模块将时间帧分解为两个Q秒,前Q秒信号送到系统u,恢复出密钥信号,后Q秒信号送到系统 ,“感应”出加密信号。在解密模块,通过加密运算f的逆运算f-1,恢复出的密钥信号对“感应”出的加密信号进行解密,获得所需的信息。为了更好更快地恢复出信息,解密出的信息再反馈到系统
,“感应”出加密信号。在解密模块,通过加密运算f的逆运算f-1,恢复出的密钥信号对“感应”出的加密信号进行解密,获得所需的信息。为了更好更快地恢复出信息,解密出的信息再反馈到系统 。
。
“信息感应”同步脉冲混沌保密通信系统无需传输加密的信息,而只传输两同步脉冲序列,从而避免时间帧拥堵的问题,并且不用将密钥信号和被加密的信息通过公共信道传输,提高了安全性。
脉冲同步混沌保密通信系统可以达到发射信号的复杂性和低冗余性这两个较理想的特性,使得低维混沌通信系统也可获得较高安全性,而且脉冲同步系统相对于连续同步而言有着较高的带宽利用率。另外,当脉冲间隔较小时,脉冲混沌同步对信道加性噪声和参数失配比连续同步混沌系统具有更好的鲁棒性。虽然一般的脉冲同步混沌保密系统存在着时间帧拥堵问题,但可以通过文中所介绍的“信息感应”脉冲同步混沌保密通信系统加以解决。
参考文献
1 Tao Yang. A survey of chaotic secure communication systems. International Journal of Computational Cognition, 2004;2(2):81~130
2 Makoto Itoh, Tao Yang, Leon O. Chua. Experimental Study of Impulsive Synchronization of Chaotic and Hyperchaotic Circuits. International Journal of Bifurcation and Chaos,1999;9(7):1393~1424
3 Tao Yang, Chai Wah Wu, Leon O. Chua. Cryptography Based on Chaotic System. IEEE Transactions on Circuit and Systems-I:Fundamental Theory and Applications,1997;44(5):469~472
4 Makoto Itoh, Tao Yang, Leon O. Chua. Conditions for Impulsive Synchronization of Chaotic and Hyperchaotic Circuits. International Journal of Bifurcation and Chaos, 2001;11(2):551~560
5 Anmar Khadra,Xinzhi Liu and Xuemin Shen. Application of impulsive synchronization to communication security. IEEE Transactions on Circuit and Systems-Ⅰ: Fundamental Theory and Applications,2003;50(3):341~351
6 兰祝刚,彭 巍,丘水生. 混沌同步方法研究. 通信技术,2000;108(1):28~31
7 刘 峰. 混沌的同步及其在保密通讯中的应用. 西安电子科技大学学报(自然科学版),2000;27(4):515~519

