一种基于感应原理的城市地下管道检查孔定位系统
2008-08-26
作者:穆向阳 汤 楠 江秀汉1
摘 要: 介绍一种用于城市各种地下管道中被覆盖的检查孔定位的检测系统。系统的传感器由探头及发射和接收电路" title="接收电路">接收电路组成。根据电磁感应原理设计了实用的探头线圈。发射电路" title="发射电路">发射电路产生发射线圈所需的激励,接收电路处理来自接收线圈的检测信号。由地面上的数据采集系统根据检测信号以及距离检测结果得到被覆盖检查孔的准确定位信息。经过实际管道中的现场实验,得到了令人满意的测试结果。
关键词: 电磁感应 检查孔 检测 数据采集
所谓检查孔是指城市中被公路或人行道路面所覆盖的各种地下管道中为方便管道维护所预留的出入口。由于年代久远等原因,有关这些检查孔位置的资料往往不是很全,而检查孔本身又会被路面沥青或其它物体所覆盖,这就给城市管道的维护检修带来了极大的困难。为了在不需要大规模开挖的情况下在几千米的管道范围内准确地找到所需要的检查孔位置,一种以闭路电视设备为核心的检查孔定位系统" title="定位系统">定位系统曾经在一些国家得到了应用。但是这种系统不仅价格昂贵,而且操作复杂,工作时需要由人工在显示器上根据图像进行实际的判断。所以对于负责地下管道维护的市政单位来说,急需一种既简单又经济实用的检查孔定位检测系统。
利用电磁感应原理的测量技术在工业中的应用由来已久。涡流无损检测技术可以用来对导电材料的材质、厚度、位移等进行在线检测。石油工业中广泛应用的感应测井技术可以对井下地层的物理性质进行分析,从而获得地下的含油气参数[1~2]。根据同样原理设计的检查孔定位系统由地下和地面两部分组成。地下部分由感应探头及其相应的电路组成;地面部分由以霍尔传感器为主的距离测量装置及以便携式计算机为主的数据采集处理装置组成。地面部分和地下部分通过电缆联接。工作时,探头由挂在它前端的钢缆拖拉以提供在地下管道中前进的动力。根据探头位置所在的环境介质的电导率及当时的距离信号,就可以得到相应的数据处理结果。由于在大多数情况下,地下管道周围土壤的电导率一般在0.01s/m~0.1s/m之间[3],而在充满空气的检查孔中,探头周围介质的电导率会下降到0.005s/m以下,所以这种方法可以很准确地为被覆盖的检查孔定位。
1 检测原理及探头的设计
感应探头中设计有发射和接收线圈,如图1所示。当发射线圈T通有恒定的交流电流时,由于电磁感应的作用,在接收线圈R中将会产生一个与发射电流频率相同、相位滞后π/2的感应电动势ex。同时发射线圈T上的交变电流周围形成的交变电磁场会在探头周围介质中产生与线圈同轴的涡流电流。同样,由交变涡流电流所形成的电磁场作用到接收线圈R上,就会产生一个与探头周围介质的导电率有关的感应电动势eR。这个由二次交变电磁场作用所产生的电动势就是定位系统所需要的检测信号。

由于直接耦合作用在接收线圈R上产生的磁通量可以表示为:

式中,nT和nR分别为发射线圈和接收线圈的匝数;S0为线圈的横截面积;I为发射线圈中的电流;μ为介质磁导率; D1为T、R两线圈之间的距离;MTR为两线圈互感系数。所以由此而产生的感应电动势为:
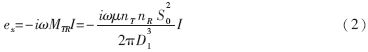
式中,ω为发射电流的频率。由式(2)可以看出,ex是一个落后于发射电流π/2且与探头周围介质导电率无关的电势信号。在系统的接收信号中,它表现为一个幅值较大的背景噪音。
在发射频率不高、介质导电率较小的条件下,可忽略电磁波传播效应和涡流损耗,用几何因子理论对接收线圈中的二次感应电动势进行计算[4],将同轴于z的两线圈周围介质中的感应涡流分割成以探头轴心为圆心、半径为r、距线圈T和R距离分别为ρT和ρR的小单元环电流。将探头周围介质看作是均匀无限介质,把所有的单元环感生的电动势叠加在一起得到:

这表明当发射电流恒定以后,k只与线圈的结构参数有关,故其被称为线圈系数。
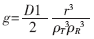
当D1确定后,g只取决于单元环相对于线圈系的空间几何位置,故其被称为单元环几何因子。由式(3)可将电导率定义为:

当σ<1时,式(5)中的积分部分也小于1。实验中取频率为20kHz时,即使将D1减少到7~8cm,式(5)所表示的比值也只能在0.8%左右。
可以通过增加一个同轴且绕向相反的补偿线圈B来抵消直耦信号的影响。为了达到这个目的,由式(2)可知,发射线圈和补偿线圈的匝数及位置应该满足:

通常情况下,地下管道中介质的实际电导率非常小。为了提高检测信号的信噪比" title="信噪比">信噪比,可以适当增加接收线圈的匝数,但过多的匝数会增加线圈的尺寸并降低检测的灵敏度。同时适当增加线圈的截面积也是提高信号信噪比的一个办法,但是也要受到几何因子理论中“线圈的尺寸要大大小于它们之间的距离”这一假设的限制。
2 检测电路设计
整个系统分为地上和地下两部分,其基本组成结构如图2所示。两大部分之间通过电缆相连接。地下部分中包括装有线圈的探头以及分别屏蔽在两个金属盒中的发射电路和接收电路。地下部分的所有装置全部固定安装在一节经过防水处理的直径为8cm左右的聚氯乙稀管内。为了防止对探头检测过程的干扰,设计时应该充分考虑地下部分的电路及导线的固定和屏蔽问题。

2.1 发射电路
发射电路的主要功能是产生具有足够功率的20kHz的正弦激励信号,同时要引出一路参考信号至接收电路,作为模拟开关" title="模拟开关">模拟开关的触发控制。由于输出功率较大,发射电路中必须解决其散热问题。
2.2 接收电路
尽管经过补偿线圈的抵消作用,接收信号中仍包含有较大的直接耦合部分。由于该部分电势在检测结果中一般保持不变且具有π/2相滞后的特征,所以探头周围介质电导率的变化就会由实际接收信号中的相位移变化体现出来。
接收电路中模拟开关的主要功能是用来检测接收信号的相位移。来自发射电路的同频率的参考信号作为模拟开关的触发控制,通过模拟开关的接收信号部分后再经过低通滤波器滤去交流分量,得到的电压信号就是一个和输入信号相角相关的量,实际上也是一个与介质导电率σ相关的量。适当调节参考信号的相位,可以得到较高的检测灵敏度。
2.3 地上部分
检测信号通过信号电缆到达地面后,首先需要滤掉传输过程中所带来的噪音。检测信号输入通道的增益和零点可以分别进行连续调节,以便适应不同的地下管道及环境。
距离测量装置由装有霍尔传感器的滑轮组及其相应的辅助电路组成。在一个塑料滑轮上装有四个小磁铁,测试电缆通过该滑轮放入井下。所以当滑轮旋转时,可通过安装在滑轮旁的霍尔传感器的脉冲个数换算出电缆长度值,作为距离信号送入计算机。
将一台带有PCMCIA A/D插卡的便携计算机作为系统的主机[5]。应用软件中首先用中值滤波法将地下传来的检测信号进行数字滤波,再将按时间采样得到的检测信号与距离信号相对应。结果可存为文件,同时也可以进行实时的图形显示。当采样数据发生满足事先设定要求的突变时,将会有相应的数据显示在界面上。
3 实验结果
3.1 实验室实验结果
实验表明,系统分辨率随线圈距离D1的增加而下降,综合考虑系统的检测灵敏度和信噪比等因素,实验样机的D1确定为0.5m。在室内环境下,样机的相位分辨率为1°,幅值分辨率为0.5%。
由于直耦电动势的值正比于ω,而涡流产生的二次电动势正比于ω2,因此当ω减小时,即使是在周围介质不变的情况下,检测信号中的相位变化也会减小,因此会降低信号的信噪比。
用不同介质对样机进行测试,实验表明,当频率低于5kHz时,信号输出对空气、干沙、湿沙等不同介质响应的区别已经很不明显。实验也表明在频率降低时,可以通过增加发射电路输出功率的方法来改善测量结果。所以在确保灵敏度、同时使系统适应大多数检测环境的情况下,实验样机发射电路输出信号的频率取为20kHz,电流幅值取为1A。
3.2 现场实验结果
现场实验在某街道中的一段长约150m、直径约8英寸的水泥下水管道中进行。管道在150m距离起始和结束处各有一处检查孔A、C。已知在二者之间还有一处检查孔B存在,但其准确位置已经被街道覆盖,无法确定。
在定位检测前,先将一带有挂钩的高压喷嘴由A孔打到C孔,同时也对管道进行了一次冲洗操作。由挂钩拖拽探头沿管道前进以进行检测。由于距离检测的方式特殊,探头前进的速度不要求恒定。
现场实验的结果如图3所示。图中曲线起始端和结束端的两处低电平为两已知检查孔A和C。63m处的低电平则是需要被定位的检查孔B的具体位置。另外,两处的高电平表明该处有某种较高导电率的介质存在。后来发现:在36m处有一段多年前因管道维修所更换的PVC管道,而52.5m处则是另一段因同样原因所更换的钢管。
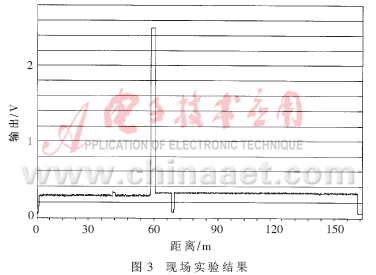
因为前进中的地下设备在钢管接头处受到了严重碰撞,由图3可以看出此后的输出信号略有漂移。这应该是由碰撞导致的内部器件相互位置的微小变化所引起的,但是并没有对检测结果造成实际影响。
现对全文总结如下:
(1)利用电磁感应原理实现了对地下管道检查孔的定位测量,系统使用方便快捷,设备简单经济,测试结果可靠,可以大大减轻市政维修的工作量。
(2)定位测量只需要对介质导电率的突变进行记录,不需要根据导电率的具体数值进行分析,所以实际系统的结构组成十分简单。
(3)采用同样的手段可以对地下不同设备或者地上设施中工作人员难以进入区域的介质变化方便地进行测量。
(4)定位中的距离测量是根据随探头放入地下的电缆长度来计算的。这样就给走向不沿街道且非直线的地下管道的定位测量带来一定困难。此时可以考虑在探头中加入电子陀螺元件。
(5)如果对系统实现数字化,可以使系统具有可变的发射频率,从而大大提高系统对测试环境的适应能力,同时也能提高信号传输的抗干扰能力。
参考文献
1 Liu Ce,L. J.Shen. Theory of a Coil-Type Resistivity Sensor for MWD Application. The Log Analyst, 1991;32(5):603~11
2 J. H. Moran, K. S. Kunz . Basic Theory of Induction Logging and Application to Study of Two-coil Sondes.Geophysics,1962;27(6):829~58
3 F. G. Bell. Electric Properties of Soils and Rocks. Boston: Butterworth & Co., 1983:8~104
4 J. R. Duesterhoeft. Propagation Effects in Induction Logging. Geophysics, 1961; 26(2):192~204
5 刘崇华.关于PCMCIA标准及应用.测控技术,1995;14(5):46~47

