1 引言
与机器进行语音交流,是人们长期以来梦寐以求的事情。语音识别技术就是让机器通过识别和理解过程把语音信号转变为相应的文本或命令的技术,其被认为是2000年至2010年间信息技术领域十大重要的科技发展技术之一。在语音识别中,当识别器的训练环境同应用环境不同时,其性能会急剧下降。为了解决这一问题,各种技术方法陆续地被提了出来,这些技术方法主要分为三大类:1)语音鲁棒特征的表达和提取技术;2)语音增强技术;3)模型补偿技术。关于这些方法的详细回顾可参见文献。本文的讨论重点是模型补偿技术。模型补偿技术主要是通过合并纯净语音模型与噪声模型,从而产生出用于识别的带噪语音模型。文献中已经证明PMC方法是一种非常有效的模型补偿方法,它能产生出具有鲁棒性的带噪语音模型,这些文献中并且给出了几种不同的PMC方法。在这些PMC方法中,一些诸如数字积分PMC(Numerical Integral PMC)和数据驱动PMC(Date—driven PMC)方法能够获得很佳的识别率,但是这些方法的运算复杂度巨大,很难运用到实际应用中去。另一方面,一些诸如对数_力口PMC(Log-Add PMC)和对数.正态PMC(Log—Normal PMC)方法通过使用较简单的估计方法来生成带噪语音模型,这样在很低信噪比的条件下识别效果不是很令人满意。其中Log-Normal PMC方法对静态模型参数给出一个严格的补偿方案,但是对动态模型参数,到目前为止只能对其均值进行简单的补偿。虽然这种动态的均值补偿可以提高识别率,但是算法仍有改进的空间,使其能够为动态的协方差参数提供补偿。
为了解决这一问题,本文提出了一种新的动态模型补偿方法(DPCM)。DPCM选定语音特征与噪声特征的差为一个新的附加随机变量,并假设该附加变量与语音和噪声特征的导数之间均相互统计独立。这样,动态特征的补偿即可通过数学的方法来解决。此外新的DPCM可以同任何已知的静态补偿方法结合生成新的带噪语音模型。实验结果也证明使用该DPCM可以提供更好的识别率。
本文定义和使用一致的域标号。上标l表示对数功率谱域,无上标的则表示Mel线性功率谱域。估计出的噪声模型参数用~标记,补偿出的带噪语音模型参数用^标记。
2 模型补偿技术
模型补偿技术是根据应用环境的背景噪声情况,通过修正纯净语音特征的统计模型产生出一个更接近真实带噪语音特征的统计模型。图1是一个基本模型补偿方案框图,输入为一个纯净的语音模型(目前一般采用HMM对语音建模)和一个估计出的噪声模型。总的来讲,模型补偿依据补偿进行的域不同可以分为两类:线性谱域补偿算法和对数谱域补偿算法。
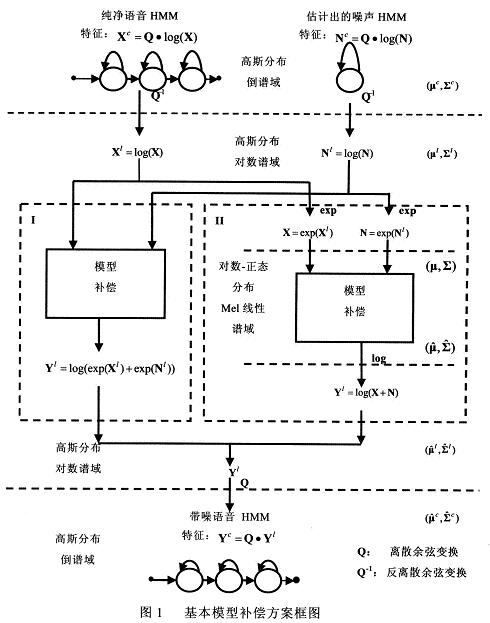
对于Log-Normal PMC(见图1-II),纯净语音模型同噪声模型的合并是在线性谱域进行。那么纯净语音和噪声模型的参数先要从倒谱域变换到对数谱域,然后再映射到线性谱域。在线性谱域进行模型的合并,然后进行相反的操作把模型参数映射变换回倒谱域。另一方面,Log—Add PMC(见图1一I)模型的补偿是在对数谱域进行。
通常的噪声信号有两类:卷积噪声(信道的频率响应)和加性噪声。在本文中仅考虑加性噪声情况。在文章中采用以下假设:1)噪声是平稳加性噪声,噪声和语音信号是相互统计独立的;2)每个子带的对数频谱域的特征(功率谱)分布被认为是(混合)高斯分布,Mel线性谱域的特征分布被认为是(混合)对数一正态分布。那么在Mel线性谱域第k个子带带噪语音特征Yk为:
![]()
其中Xk和Nk分别是线性频谱域的纯净语音和噪声子带特征(“观测”)。g是调节噪声和语音的缩放比例因子,为了表达简单起见,在后面的算法公式中省略此缩放比例因子g。那么对数频谱域子带的带噪语音特征Ykl同纯净语音特征Xkl和噪声特征Nkl的失配函数为:
![]()
2.1 静态特征补偿
对于Log-Normal PMC静态模型特征补偿的核心算法是对数谱域与线性谱域之间的非线性映射同线性谱域模型的合并,即:
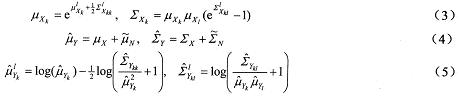
其中k、l分别为第k、l个子带。
对于Log—Add PMC静态模型特征补偿的只对均值进行补偿:
![]()
2.2 动态特征补偿
由于推导出严格的Log—Normal PMC动态特征补偿算法非常困难,目前对Log—Normal PMC的动态特征补偿一般采用粗略的补偿方法,只对其均值进行补偿。
![]()
对于Log-Add PMC其动态特征补偿算法为:
![]()
3 新的动态模型参数补偿方法
在本文中,使用静态“观测”的时间导数作为动态的“观测”。这样,动态特征的失配函数就应等于静态特征的失配函数的一阶导函数。根据(2),动态特征失配函数为:
![]()
定义一个附加的随机变量Zkl,定义为Zkl=Nkl一Xkl。由于Nkl和Xkl均为正态分布,并且他们之间相互独立,那么随机变量Zkl也是一个正态分布。其的均值和方差分别可以表示为μZkl=μNkl-μXkl和![]() 那么动态失配函数(9)就可以进一步改写成含Zkl的函数。
那么动态失配函数(9)就可以进一步改写成含Zkl的函数。
![]()
由于假设背景噪声为平稳加性噪声,那么噪声动态特征的均值就可以被近似为零。本文还假设附加的随机变量同语音和噪声的动态特征不相关。这个假设也是DPCM的核心本质假设。由于静态特征与其微分变换量之间是松相关的,所以这个假设是比较合理的。
3.1 均值补偿
依据失配函数(10)和上述假设,对数谱域的带噪语音特征的统计均值为:

其中

参数ti和ωi(i=l~n)是Hermite多项式Hn(t)的横坐标和对应的权值。
3.2 协方差补偿
同样根据(10)和相关假设,可以获得对数谱域的带噪语音特征的协方差补偿算法。
![]()
其中
且
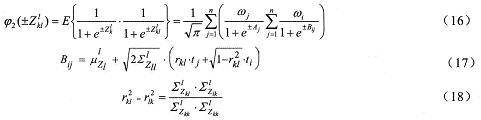
附加随机变量Zkl的引入以及附加随机变量与语音和噪声的动态特征不相关假设的使用降低了动态模型补偿问题的求解维数。这种维数的降低同Gauss-Hermite数字积分的应用,使得新的DPCM成为一种十分有效的动态模型补偿方法。
4 算法评估
算法评估实验采用基于孤立字的6状态HMM来做识别器。每个状态有4个高斯密度函数。选取24个MFCC(12个静态特征,12个动态特征)作为语音特征。训练阶段,用纯净语音训练出纯净语音模型。在识别阶段,使用纯净语音模型作为基本模型来识别。
使用TI—digits为算法评估语音库,选用数据库中有16个人(8男8女)的5081个短句,其中包含20个孤立词,数字‘0’到‘9’和10个附加命令如‘go’、‘help’、‘repeate’等。训练集含有641句,测试集包括5081句。算法分析窗口的长度为32ms,帧速率为9.6ms/帧。选取NOISEX-92中的White、Pink和Destoryerengine 3种噪声作为评估的环境噪声。使用200帧非重叠的噪声来估计噪声模型。全局信噪比定义为:
![]()
其中Pm(k)是第m帧的纯净语音功率普,N(k)是估计的噪声能量平均谱,H是每句的语音帧数,L是FFT的长度,g是缩放因子让所加的噪声符合指定的全局信噪比。带噪语音由(20)生成。
![]()
其中y(i)是带噪语音,x(i)和n(i)分别是纯净语音和噪声。对于文中语音的动态特征参数是依据(21)获得。
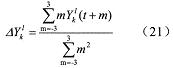
为了比较DPCM方法的性能,采用5种识别方法:失配情况下的识别,Log—Add PMC,Log—Normal PMC,以及Log-AddPMC与Log—Normal PMC和DPCM相结合的方法。
图2给出了White Noise环境下Gauss—Hermite积分项数n与识别率及算法复杂度关系。从图中可以看出随着积分项n的增加,两种方法的识别率都没有明显的变化。但是算法的复杂度却随着n的增加而增加。结果说明n=2的Gauss—Hermite积分可以提供足够的计算精度。因此在DPCM 中采用n=2, 即
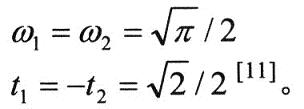
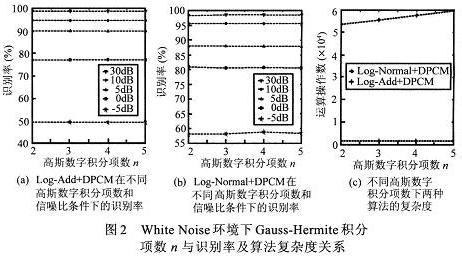
表1~表3列出的是在不同噪声环境和信噪比条件下的各种算法的识别率。可以看出使用补偿算法的识别率比失配情况下有很大的提高。在-5dB条件下,使用了DPCM的识别方法对各种噪声语音的平均识别率比仅使用Log—Add PMC和Log—NormalPMC的方法有绝对的7.5%和6.6%增加,在0dB情况下绝对增加值分别为8%和7.3%。在信噪比5—10dB下,有含DPCM方法的识别率比其他两种算法仍然有性能上的提高。
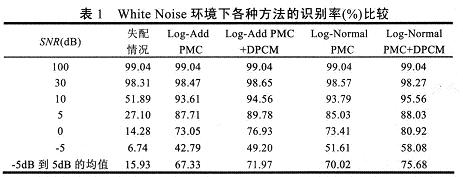
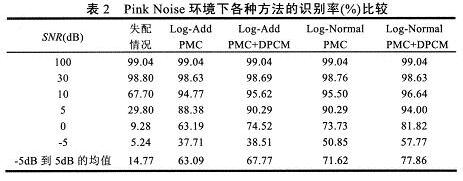
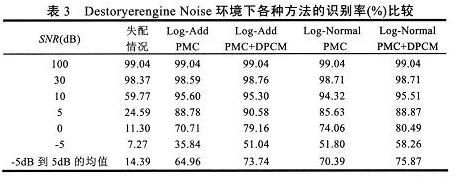
表4列出了更新每个状态的4个高斯密度分布中的单个高斯密度分布时,静态均值和方差以及动态均值和方差(注:Log—Add PMC算法只对均值补偿)从倒谱域变化到对数谱域、在对数谱域进行模型补偿、以及从对数谱域变回倒谱域所需的乘法、除法、指数运算以及对数运算的次数。其中N和M分别表示在倒谱域和对数谱域特征的维数。从表中可看出含有DPCM的算法复杂度比其原始算法的复杂度只有轻微的增加。

实验证明了本文的DPCM算法可以处理在不同加性噪声环境下的语音识别任务,并且能够取得比较好的识别效果。性能的提升归功于相对应比较准确的动态模型补偿方法的应用。通过这种方法的使用,含DPCM算法的识别率比目前的PMC算法有较明显的提升。
5 结论
文中提出了一种新的动态特征补偿方法,并给出了反映加性噪声的语音动态特征失配函数,以及在此基础上依据合理的假设,推导出的一系列动态模型参数补偿DPCM的算法公式。并且DPCM算法可以与任意的静态模型补偿算法结合以提高原始算法的识别率。实验结果表明在不同的噪声环境下结合DPCM的PMC算法可以给出比原始PMC算法具有更好的识别率,在低信噪比条件下提升效果更为明显。此外结合DPCM的模型补偿算法的复杂度与原补偿算法的复杂度基本相当,只有轻微的增加。可见DPCM算法是一种非常有效的动态特征补偿算法。

