噪声的重要特性之一就是其频谱密度。电压噪声频谱密度是指每平方根赫兹的有效(RMS) 噪声电压（通常单位为nV/rt-Hz）。功率谱密度" title="功率谱密度">功率谱密度的单位为W/Hz。在上一篇文章中，我们了解到电阻的热噪声" title="热噪声">热噪声可用方程式 2.1 计算得出。该算式经过修改也可适用于频谱密度。热噪声的重要特性之一就在于频谱密度图较平坦（也就是说所有频率的能量相同）。因此，热噪声有时也称作宽带噪声" title="宽带噪声">宽带噪声。运算放大器也存在宽带噪声。宽带噪声即为频谱密度图较平坦的噪声。 

方程式 2.1：频谱密度——经修改后的热噪声方程式 

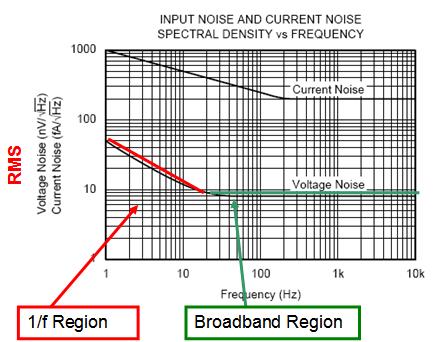
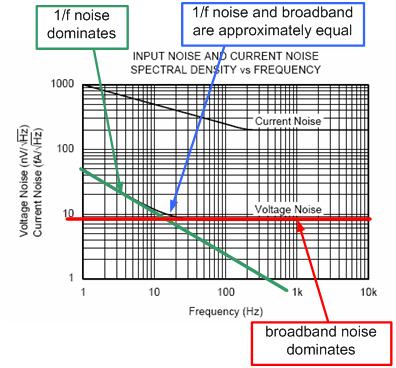
图 2.1：运算放大器噪声频谱密度 

除了宽带噪声之外，运算放大器常还有低频噪声区，该区的频谱密度图并不平坦。这种噪声称作 1/f 噪声，或闪烁噪声，或低频噪声。通常说来，1/f 噪声的功率谱以 1/f 的速率下降。这就是说，电压谱会以 1/f^{(1/2 )} 的速率下降。不过实际上，1/f 函数的指数会略有偏差。图 2.1 显示了典型运算放大器在 1/f 区及宽带区的频谱情况。请注意，频谱密度图还显示了电流噪声情况（单位为 fA/rt-Hz）。 

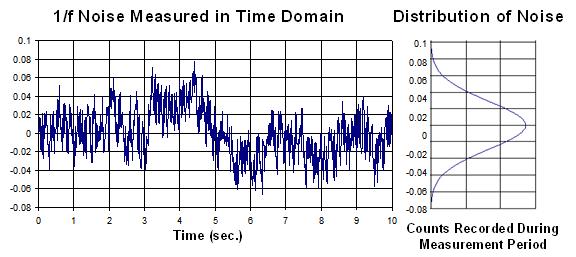
我们还应注意到另一点重要的情况，即 1/f 噪声还能用正态分布曲线表示，因此第一部分中介绍的数学原理仍然适用。图 2.2 显示了1/f 噪声的时域情况。请注意，本图的 X 轴单位为秒，随时间发生较慢变化是1/f 噪声的典型特征。 

图 2.2：时域所对应的 1/f 噪声及统计学分析结果 

图 2.3 描述了运算放大器噪声的标准模型，其包括两个不相关的电流噪声源" title="噪声源">噪声源与一个电压噪声源，连接于运算放大器的输入端。我们可将电压噪声源视为随时间变化的输入偏移电压分量，而电流噪声源则可视为随时间变化的偏置电流分量。 

图 2.3：运算放大器的噪声模型 

运算放大器噪声分析方法 

运算放大器噪声分析方法是根据运放数据表上的数据计算出运放电路峰峰值输出噪声。在介绍有关方法的时候，我们所用的算式适用于最简单的运算放大器电路。就更复杂的电路而言，这些算式也有助于我们大致了解可预见的噪声输出情况。我们也可针对这些更复杂的电路提供较准确的计算公式，但其中涉及的数学计算将更为复杂。对更复杂的电路而言，或许我们最好应采用三步走的办法。首先，用算式进行粗略的估算；然后，采用 spice 仿真程序进行更准确的估算；最后通过测量来确认结果。 

我们将以 TI OPA277 的简单非反向放大器为例来说明有关电路的情况（见图 2.4）。我们的目标是测定峰峰值输出噪声。为了实现这一目的，我们应考虑运算放大器的电流噪声、电压噪声以及电阻热噪声。我们将根据产品说明书中的频谱密度曲线来确定上述噪声源的大小。此外，我们还要考虑电路增益与带宽问题。 

                    图 2.4：噪声分析电路示例 

首先，我们应了解如何将噪声频谱密度曲线转换为噪声源。为了实现这一目的，我们需进行微积分运算。简单提醒一句，积分函数确定曲线下方的面积。图 2.5 显示，我们只须将长宽相乘（即矩形区域面积），便能获得常数函数的积分。这种转换频谱密度曲线为噪声源的关系比较简单。

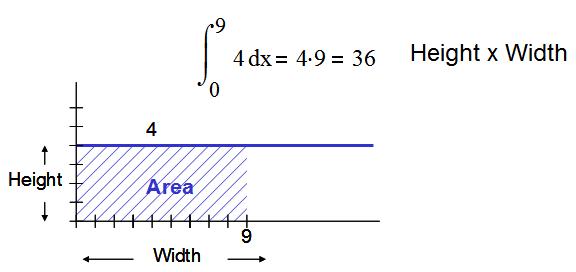
                                          图 2.5：通过积分计算曲线下方面积 

人们通常会说，只有将电压频谱密度曲线进行积分计算，才能得到总噪声值。事实上，我们必须对功率谱密度曲线进行积分计算。该曲线实际反映的是电压或电流频谱密度的平方（请记住：P = V²/R 且 P=I²R）。图 2.6 显示了对电压频谱密度曲线进行积分计算所得的奇怪结果。图 2.7 显示，您可将功率谱密度进行积分计算，再通过求结果的平方根将其转换回电压。请注意，我们由此可获得合理结果。 

                                       图 2.6：计算噪声的不正确方法 

                                                       图 2.7：计算噪声的正确方法 

通过对电压与电流频谱的功率谱密度曲线进行积分计算，我们可得到运算放大器模型信号源的 RMS 幅度（图 2.3）。不过，频谱密度曲线将分布在 1/f 区与带低通滤波器" title="低通滤波器">低通滤波器的宽带区（见图 2.8）。如计算上述两个区域的总噪声，我们要采用微积分计算推导出的算式。再根据第一部分所讨论的处理非相关信号源的方法，对上述两个计算的结果做和的平方根 (RSS) 运算，对应第一部分中提到的非相关信号源。 

首先，我们要对带低通滤波器的宽带区域进行积分计算。理想情况下，曲线的低通滤波器部分是一条纵向直线，我们称之为砖墙式滤波器 (brick wall filter)。由于砖墙式滤波器情况下的曲线下方区域为矩形，因此这一区域的问题比较好解决，长乘宽即可。在实际情况下，我们不能实现砖墙式滤波器。不过，我们可用一组常量来将实际情况下的滤波器带宽转换为等效的砖墙式滤波器带宽，以满足噪声计算的需要。图 2.9 将理论砖墙式滤波器与一阶、二阶及三阶滤波器进行了对比。 

                               图 2.8：带滤波器的宽带区 

图 2.9：砖墙式滤波器与实际滤波器相比较 

我们可用方程式 2.2 用于转换实际滤波器或做砖墙式滤波器等效。表 2.1 列出了各阶滤波器的换算系数 (K_n)。举例来说，一阶滤波器带宽乘以 1.57 即为砖墙式滤波器带宽。调节后的带宽有时也称作噪声带宽。请注意，换算系数随着滤波器阶数的提升将越来越接近于1。换言之，滤波器阶数越高，就越接近于砖墙式滤波器。 

方程式 2.2：宽带区域上简单滤波器的噪声带宽 

表 2.1：砖墙式滤波器校正系数 

既然我们有了将实际滤波器转换为砖墙式滤波器的算式，那么我们就能很方便地进行功率频谱的积分运算了。请记住，功率的积分运算为电压频谱的平方。我们需将积分结果进行平方根运算转换回电压。方程式 2.3 即由此得出（见附录 2.1）。因此，根据产品说明书中的数据套用方程式 2.2 、方程式 2.3便可计算出宽带噪声。 

方程式 2.3：宽带噪声方程式 

我们需记住，我们的目标是测定图 2.3 中噪声源 Vn 的幅度。该噪声源包括宽带噪声与 1/f 噪声。我们用方程式 2.2 与 2.3 可计算出宽带噪声。现在我们应计算 1/f 噪声，这就需求对噪声频率密度图 1/f 区域的功率频谱进行积分计算（如图 2.10所示）。我们可用方程式 2.4 和 2.5 获得有关积分结果。方程式 2.4 将 1/f 区的噪声测量结果归一化为 1Hz 时的噪声。某些情况下，我们可从图中直接读出该数值，有时用方程式更方便求得（见图 2.11）。方程式2.5用归一化噪声、上部噪声带宽与下部噪声带宽来计算 1/f 噪声。附录 2.2 给出了整个演算过程。

                               图 2.10：1/f 区域 

方程式 2.4：频率为 1Hz 时的噪声 （归一化） 

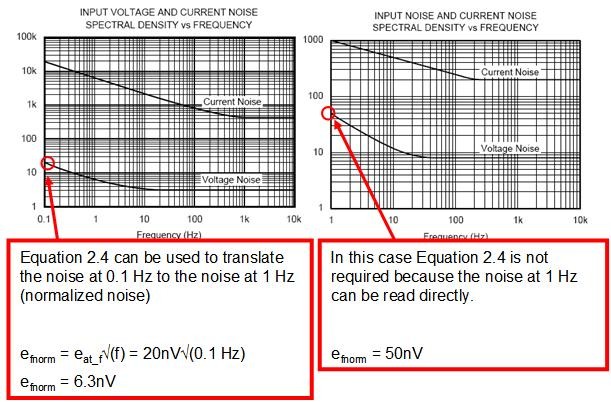
                                             图 2.11：两个 1/f 归一化示例 

方程式 2.5：1/f 噪声计算 

在考虑 1/f 噪声时，我们必须选择低频截止点。这是因为 1/f 函数分母为零时无意义（即 1/0 无意义）。事实上，理论上 0 赫兹时噪声趋近于无穷。但我们应当考虑到，频率极低时，其相应的时间也非常长。举例来说，0.1Hz 对应于 10 秒，而 0.001Hz则对应于 1000 秒。对极低的频率而言，对应的时间有可能为数年（如 10nHz 对应于 3 年）。频率间隔越大，积分计算所得的噪声就越大。不过我们也要记住，极低频噪声检测需要很长时间。我们在以后的文章中将更详细地探讨此问题。目前，我们暂且记住这一点，1/f 计算时通常用 0.1Hz 作为低频截止点。 

既然我们已得到了宽带与 1/f 噪声的幅度，现在就用第一部分给出的无相关噪声源算式来叠加噪声源 （见如下方程式 2.6 与本系列文章的第一部分中的方程式 1.8）。 

方程式 2.6： 1/f 与宽带噪声叠加结果 

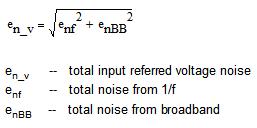
工程师考虑分析方法时通常会担心，1/f 噪声与宽带噪声是否应在两个不同的区域进行积分计算。换言之，他们认为，由于 1/f 噪声与宽带噪声相加后会超出 1/f 区域，从而出现错误。实际上，1/f 区域与宽带区域一样，都涵盖所有频率。我们必须记住，当噪声频谱显示在对数图上，1/f 区在降至宽带曲线以下后影响极小。两条曲线结合明显的唯一区域就在 1/f 半功率频点处。在此区域中，我们看到两区域结合部的情况与数学模型相同。图 2.12 显示了两区实际重叠的情况，并给出了相应的幅度。 

                   图 2.12：1/f 噪声区与宽带区重叠 

现在，我们已得到了将噪声频谱密度曲线转换为噪声源所需的全部方程式。请注意，现在我们已推算出了电压噪声所需的方程式，不过相同的方法也可运用于电流噪声的计算。在本系列随后的文章中，我们将讨论用有关方程式来解决运算放大器电流的噪声分析问题。 

本文总结与下一篇文章简介 

在噪声系列文章中，本文介绍了运算放大器的噪声模型与噪声频谱密度曲线。此外，我们还介绍了基本的噪声计算方程式。本系列的第三部分将用实例说明实际电路中的噪声计算过程。 

致谢！ 

特别感谢以下人员提供的技术意见 

 TIBurr-Brown 产品部： 

Rod Bert，高级模拟 IC 设计经理 

Bruce Trump，线性产品经理

Tim Green，应用工程设计经理

Neil Albaugh，高级应用工程师

参考书目

Robert V. Hogg 与 Elliot A Tanis 共同编著的《概率与统计推断》，第三版，麦克米兰出版公司 (Macmillan Publishing Co.)出版； 

C. D. Motchenbacher 与 J. A. Connelly 共同编著的《低噪声电子系统设计》，Wiley-Interscience Publication 出版。 

关于作者：

Arthur Kay是 TI 的高级应用工程师。他专门负责传感器信号调节器件的支持工作。他于 1993 年毕业于佐治亚理工学院 (Georgia Institute of Technology)并获得电子工程硕士学位。他曾在 Burr-Brown与 Northrop Grumman 公司担任过半导体测试工程师。 

附录 2.1： 

附录 2.2： 

一阶滤波器“砖墙”校正系数的演算过程。