Chirp信号又称为线性调频信号，它作为大时宽带宽积信号广泛应用于雷达、声纳和地震勘探等系统中。近年来逐步得到超宽带研究领域的广泛关注，并以其独特优势成为标准之一,即Chirp-UWB[1]。COTR-UWB(Code-Orthogonalized Transmitted-Reference Ultra-Wideband)[2]是Chirp-UWB的一种具体实现方案。该方案中模板信号每个符号周期内有一个Chirp信号码片，然后用数据信号对其进行COTR调制。经过信道传输后，接收端用与发射端相同的模板信号进行相干检测并估计出多径时延，然后通过多径合并和COTR解调恢复出数据。系统如图1所示。

    实际无线环境中，多径时延会导致相干检测后的信号频谱出现伪尖峰，影响多径判别及时延估计，最终影响数据恢复。传统的时延估计采用相关法[3]，主要基于信号平稳这个假设，而Chirp信号是非平稳信号，因而此类方法可靠性不高。当多径时延存在时，要先求出峰值所在的位置，然后通过多次判断求出正确时延。本文提出一种能够判别伪尖峰的时延估计方法。该方法通过双阶段变换积累Chirp信号能量并利用时延特征判别伪尖峰。第一阶段利用Chirp信号在时频域良好的能量聚集性进行能量积累，然后在完成时频能量积累阶段后转换到第二阶段即参数能量积累阶段。在完成参数能量积累阶段的同时，利用时延特征信息判别伪尖峰并求出时延。文中在两个阶段分别采用了RSPWVD和Hough变换。RSPWVD能在抑制交叉项的同时使Chirp信号能量集中在时频域的多条直线上[4]，非常适合分析处理Chirp非平稳信号。然后采用Hough变换把待检测时频域信号特征转换为参数空间点的能量积累。在参数空间中，噪声点或孤立点是随机的，并不能得到有效的能量积累，因而其数值很小，而直线上的点对参数空间中的信号特征都有贡献，可以达到能量积累的效果。仿真实验表明，本文方法在经过双阶段能量积累后利用时延特征信息可以消除伪尖峰的影响，从而正确地估计多径时延。
1 伪尖峰发生机理
　图1中的相干检测采用与发射信号相同的参考信号和接收信号相乘，如图2所示。

   假设收发双方存在时延差，接收信号相对于参考信号延时τ(图2仿真时τ=0.2 s,T=1 s)，Chirp信号可表示为s(t)=Acos(2πf₀ t+πμt²)，其中幅度A=1，起始频率f₀=0，μ为调频率。图3是假设每个符号存在3条径时出现伪尖峰的频谱图，图3(b)图是图3(a)图的局部放大图。3条径时延分别为0.2 s、0.3 s、0.4 s；起始扫频频率f₀ =0；扫频周期T=1 s；μ=1 000；抽样频率f_s=10 000 Hz。可以看出伪尖峰出现的位置与推导一致。本文的工作就是判别伪尖峰从而正确地估计时延。

2  算法原理
    针对多径时延导致伪尖峰影响时延估计的问题，本文提出的方法利用双阶段变换思想,分阶段积累Chirp信号能量。首先利用Chirp信号在时频域良好的能量聚集性进行能量积累，然后在完成时频能量积累阶段后转换到参数能量积累阶段。当完成参数能量积累阶段的同时利用时延特征信息消除伪尖峰影响而造成的时延估计误判，从而正确地估计多径时延。下面详细介绍算法原理和算法实现，流程如图4所示。

2.1 RSPWVD变换下的时频能量积累及其信号表征
    时频能量积累阶段采用的RSPWVD是WVD变换的改进，非常适合分析Chirp信号。参考信号和接收信号相乘后的信号为：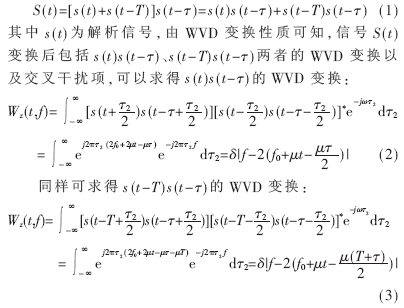

    可以看出，在WVD变换后的时频域上，信号能量聚集在两条直线上，表达式如式(4)所示。

　可以看出，原时频(X,Y)平面上的点对应参数空间中的一条正弦曲线，且直线上的点对应的参数空间的曲线都相交于同一点。因此，Hough变换通过在参数空间对相交点进行累加统计就可以检测时频(X,Y)平面上能量分布聚集成的直线。通过搜索局部极大值并从具有极大值的相交点的坐标就可获得调频率和时延的信息，关系式如式(8)所示。

3 仿真实验
    仿真实验Chirp信号为解析信号,表示为Aexp(j(2πf₀ t+πμt²))，扫频起始频率f0为0 Hz，频率f使用归一化频率，取值范围为[0,0.5]，信号幅度A=1；频带宽B=200 Hz；扫频时间T=1 s；调频率μ=B/T；抽样频率为f_s=1 000 Hz，噪声采用高斯白噪声，SNR=5 dB；假设存在一条径，时延τ=0.3 s，并改变τ值进行多次实验。
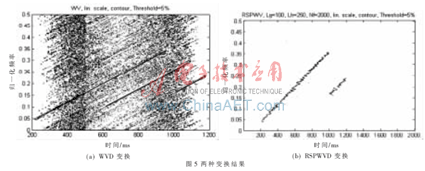
    时频能量积累阶段采用RSPWVD变换抑制交叉项，门限设置为平均能量值的0.1倍，这样可以减少运算时间，而又不至于丢失信息影响检测。之后参数能量积累阶段采用Hough变换，门限设为最大值的5%以降低数据处理量。图5(a)、图5 (b)分别是WVD和RSPWVD图。可以看出，RSPWVD能够抑制交叉项同时保持信号良好的能量聚集性。在Hough变换后参数空间有两个明显的峰值，相应地在(ρ,θ)平面上有两个明显的能量聚集点，其θ轴坐标是相等的。在ρ轴方向上靠近原点(坐标绝对值小)的那个能量聚集点表征了正确的时延。因此，只要对经过Hough变换后的能量聚集点进行检测，聚集点中ρ绝对值小的即表征了正确的时延，由图6(a)、图6(b)可以看出对应的轴坐标是相等的,表1是实验结果。

　 针对多径时延导致的伪尖峰影响时延估计的问题，文中基于双阶段变换积累Chirp信号能量的思想提出了一种估计时延的方法。该方法分阶段积累Chirp信号能量，利用Chirp信号在时频域有良好的能量聚集性，在完成时频能量积累阶段后转换到参数能量积累阶段。当完成参数能量积累阶段的同时消除了伪尖峰的影响，避免了此影响造成的时延估计误判，从而正确地估计多径时延。时频能量积累阶段中，在采用RSPWVD变换能在抑制交叉项的同时使Chirp信号能量聚集为时频域上的多条直线。参数能量积累阶段采用Hough变换把待检测时频域信号特征转换为参数空间点的能量积累，即通过在参数空间里对相交点进行累加统计完成参数能量积累。最后通过搜索局部最大值及利用时延特征信息消除伪尖峰的影响，进而求出多径时延，并通过设置两次门限降低运算时间。仿真结果表明，该算法可以适应于具有同样信号特征的场合，且计算复杂度低，在低信噪比的条件下仍能工作。
参考文献
[1]  Chirp modulation confirmed for IEEE standard. Available: http://www.nanotron.com EN/NE_releases_2006-10-09.php.
[2]  ZHANG Jian, HU Han Ying, LIU Luo Kun，et al. Codeorthogonalized transmitted-reference ultra-wideband(UWB)  wireless communication system. Wireless Communications Networking and Mobile Computing,2007,Wicom2007.International conference on Volume,ISSue,21-25, 2007,9:528-532.
[3]  行鸿彦, 唐娟. 时延估计方法的分析[J]. 声学技术, 2008,27(1):110-112.
[4]  梁红,胡旭娟,朱云周.基于RSPWVD的多分量FM信号盲分离[J].火力与指挥控制, 2008,33(11):92-94.
[5]  苏峰,何友,曲长文,等.基于修正的伪WVD和Hough变换的二值积累的信号检测方法[J].电子与信息学报,
2004,26(12):1916.
[6]  刘建成,杨建华,周杰等.基于Wigner-Hough变换的线性调频信号检测性能[J].信号处理,2005,21(4A):546-549.