1 生成均匀分布噪声
    设x(1),…,x(k)是给定的k个随机数,在(-X,X)内均匀分布,相互独立。第k+1个随机数由x(1)和x(k)按照模X相加得到:

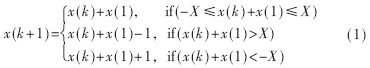
    即x(k+1)仍然是(-X,X)之间的随机数。在下一次运算时,将x(k+1)移到x(k)的位置,x(k)移到x(k-1),……,x(2)移到x(1),然后再做模X运算,相加得到x(k+2),如此循环,产生序列{xn}。
    首先讨论上面的模X运算。对于采用补码运算的处理器而言,只要取X为处理器字长,则在不考虑进位的情况下,通常的加法就是模加运算。
    然后采用数据结构实现上面的循环机制。设两个指针:头指针head和尾指针tail。每计算完一次噪声值后,两个指针都要向下移动一个位置。已到序列尾部,则重新指到序列的头部,即按照加1模K运算:
    head=(head+1)mod(K)
    tail=(tail+1)mod(K)
    为了计算方便,选K为256。若用head和tail指针做相对偏移地址,则可以采用1个字节存储。加1运算之后若不考虑溢出,就等价于加1模256操作。
2 映射高斯噪声
    为了由均匀噪声快速产生高斯噪声,采用了映射函数法。其算法原理如图2所示。

    将正态分布函数的自变量y进行合理的离散化,得到一系列函数值,构成一个数列。再将此数列中的任一个数y_i映射到数轴x上的某个小区间段[x_i0,x_i1],其中||x_i1-x_i0||=y_i。取遍数列中所有的数值,得到一系列的小区间。将所有的小区间依次连接起来,中点置于数轴的零点,则构成变量x的取值区间[-x,x]。将数轴x上的各个小区间与y序列建立映射关系,则可以证明,如果采样间隔足够小,那么x域中的随机分布将对应于y域中的高斯分布" title="高斯分布">高斯分布。
    这个映射关系可以函数表示为:y=f(x)。
    其中x服从(-X,X)区间内均匀分布,而y服从均值为u、方差为σ的高斯分布。f函数曲线如图3所示。

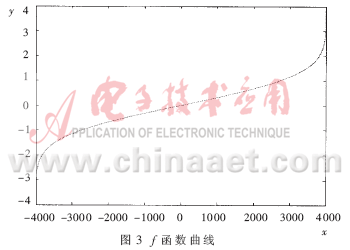
    在算法实现时,对y对应的高斯分布值进行量化处理,并为x分配一块连续的内存区域[0,2X],每个内存单元的(偏移地址-X)值代表了x值大小,单元内容存放了该单元对应的y值。这片内存区域就是所需要的映射查找表。这个表具有通用性,可以预先计算好,在需要时可以直接使用,不必再计算。
    对于(0,1)正态分布,图4中的z_i都小于1,没有实际意义,所以将其放大了200倍: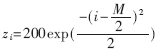

    则原始映射表描述为:

    原始映射表比较大,实际使用时对其做了粗采样。对y对应的高斯分布值进行的量化也没有采用图4中的标准阶梯形式,而是采用了如下粗采样形式:
   

    其中:采样间隔d=Σ_yj/M,量化处理曲线如图5所示。

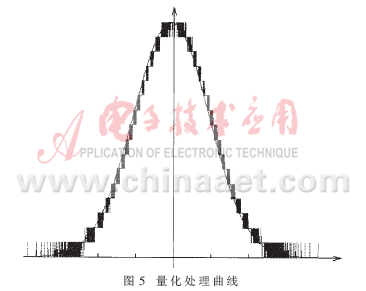
    从图5可以发现,两边较小处并没有像阶梯图那样截止为0,而是允许以小的概率出现非零值。试验证明这种方式更好一些。
    考虑高斯分布的实际情况,并经过试验验证y仅在[-4,4]之间取值,就能够达到令人满意的精度。图6给出了X大小对噪声精度的影响曲线,纵轴为平均误差。

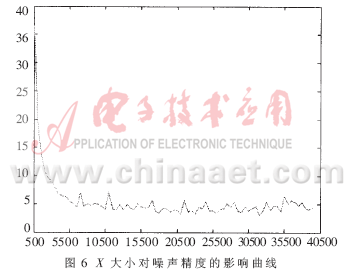
    可以看出,当2X大于5500时,误差达到了极小稳定状态。为了方便计算,选择2X=2¹³=8192,即X=2¹²=4096。
    图7给出了实验结果(均值为120,方差为40):虚线部分为标准高斯分布的曲线,实线部分为噪声直方图,验证了本方法的有效性。