摘 要: 针对概率神经网络的输入量过多会影响其训练速度的问题,采用了基于分辨矩阵的粗糙集属性约简方法,删除不相关或不重要的指标。鉴于空气质量分级标准的模糊性,将模糊数学和概率神经网络结合起来,构建了模糊概率神经网络空气质量评价模型(FPNN),然后将约简后的指标值进行模糊化处理后输入到PNN神经网络进行智能训练。实例表明,该方法提高了收敛速度,评价结果客观可靠,具有一定的实用价值。
关键词: 粗糙集;概率神经网(PNN);分辨矩阵;空气质量
随着科技和经济的迅速发展,工业废气、机动车尾气、尘埃等急剧增加,成为空气质量下降的污染源,对人们的身体健康构成了严重威胁,因此采取控制和改善空气质量的有效措施,合理地进行空气质量评价及预测成为当前环境科学研究的重要内容之一。
常规的空气质量评价方法有:API法、灰色聚类法、模糊综合评价法及模糊灰色模型等。但这些方法都存在着一些不足,如评价结果或多或少受主观因素的影响。近年来,有人把神经网络应用到空气质量评价上并取得了较好的效果。人工神经网络ANN(Artificial Neural Nets)具有较强的非线性映射、自学习、自适应及容错能力,它能模拟大脑的思维,利用存储的网络信息对未知样本进行评价。
模糊数学是研究和处理自然界与信息技术中广泛存在的模糊现象的数学(其中的相对隶属度能很好地表示模糊概念的相对状态),但它很难表示时变知识和过程,而神经网络能够通过自学习功能来获得精确的或模糊的知识,两者的融合即模糊神经网络,弥补了模糊数学在学习方面的不足和神经网络在处理模糊数据方面的缺陷。
粗糙集理论是一种处理不完整和不确定知识的数学工具,它是Z.Pawlak于1982年提出的。粗糙集能有效地分析和处理不精确和不完整等各种不完备信息,并从中发现隐含的规律。
本文把粗糙集理论和模糊概率神经网络知识运用到空气质量评价过程中,简化了网络模型,提高了评价效率和评价结果的客观性。
1 对粗糙集模糊概率神经网络的描述
1.1 粗糙集属性约简问题
知识约简是粗糙理论的重要内容之一,即求出信息系统的原有属性集合的一个极小子集,且该子集具有与原属性集合相同的分类能力,这样既保证了分类的质量,也提高了分类的速度。

1.2 指标相对隶属度矩阵
若空气质量有b个级别,c项评价指标,则这c项指标对应的b级评价标准构成了空气质量评价的标准值矩阵:

1.3 基于粗糙集模糊概率神经网络的空气质量评价模型的框架结构
与常用的BP神经网络相比,概率神经网络(PNN)是一种结构简单、训练速度快、非线性映射能力强且具有较好分类能力的神经网络模式。但若PNN有多个输入或大量的训练样本数据,分类结果的准确性就可能降低,同时也降低了网络的训练速度。因此需要运用粗糙集理论中的知识约简算法对属性进行约简,也就是在保证知识表达系统在分类能力不变的条件下,删除不重要或不相关的条件属性,减少PNN的输入神经元的个数,从而提高训练速度。
为了使整个评价模型的指标具有可比性,采用了模糊数学理论中的相对隶属度的知识,对约简后的评价标准数据进行预处理,并构造相对隶属度矩阵,这样就能较清晰地反映空气质量评价中的各指标的相对状态,并在此基础上构建模糊概率神经网络(FPNN)模型。
根据粗糙集和FPNN模型对问题分析的思路,空气质量评价模型的框架结构可以用图1所示的流程图描述。

2 基于粗糙集FPNN空气质量评价模型的实例
2.1 指标体系的建立
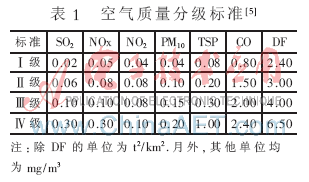
指标体系的选择直接影响到评价结果的准确性,若评价指标太多,就会延长神经网络训练的时间,若指标太少,就可能降低评价结果的准确性。根据中华人民共和国国家标准(GB3095-1996《环境空气质量标准》及2000年的[2000]1号文件)及我国空气污染的特点可知,影响我国空气质量的评价指标有:SO2、NOx、TSP(悬浮颗粒物)、PM10、DF(降尘)、NO2、CO。
2.2 粗糙集属性约简
2.2.1 属性约简的步骤
粗糙集理论只能处理离散的数据,因此需要进行连续属性的值离散化,它可以由领域专家根据经验给出相应的区间,也可以根据某种原则对空间进行划分,给出离散点进行离散化。本文采用后者。区分矩阵法是计算决策表属性约简的常用方法,但它没有充分考虑到数据的不相容度,只适用于相容决策表。下面给出最佳属性约简算法的步骤:
(1)连续数据的离散化;
(2)构造分辨矩阵M=[mij]n×n;
(3)确定D的C正域POSC(D),可按照文献[3]所提出的简便方法来快速确定POSC(D);
(4)判断C中各属性ci是否对D可约简,方法是当去掉属性ci时,检验正域POSC(D)≠POSc-(ci)(D)是否成立。若成立,则ci不可约简,否则,ci可约简[4];
(5)按步骤(3)~(4)遍历所有属性;
(6)所有不可约简的属性集合为约简后的指标,即条件属性C对于决策属性D的一个相对约简。
2.2.2 空气质量评价指标的约简
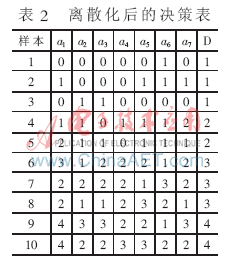
为了更清楚地了解空气的质量状况,在三级基础上增加一级,即将空气质量划分为四个等级,分别为:Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级。选取10个城市的数据,这10个城市污染差别显著,可以作为属性约简的样本(篇幅有限,此数据不再列出)。令a1、a2、a3、a4、a5、a6、a7分别表示条件属性(空气质量评价指标)中的:SO2、NOx、NO2、PM10(可吸入颗粒物)、TSP(总悬浮颗粒物)、CO、DF(降尘)。然后对属性值进行离散处理:令xik为第i个样本第k项指标值,yjk为第k项指标的第j级标准值,pk为所取样本的第k项指标离散处理后的值。当xik≤y1k时,pk=0;当y1k<xik≤y2k时,pk=1;当y2k<xik≤y3k时,pk=2;当y3k<xik≤y4k时,pk=3;当xik≥y4k时,pk=4。其中我国空气质量分级标准如表1所示。决策属性D的属性值与空气质量等级的对应关系是:1——Ⅰ级,2——Ⅱ级,3——Ⅲ级,4——Ⅳ级,这样可得到离散化后得到的决策表如表2所示。然后根据公式(1)建立分辨矩阵(篇幅有限,不再显示),应用属性约简的步骤(3)~(6),最后得到约简后的指标是:SO2、NO2、TSP、PM10。
2.3 相对隶属度矩阵的建立及FPNN的仿真研究
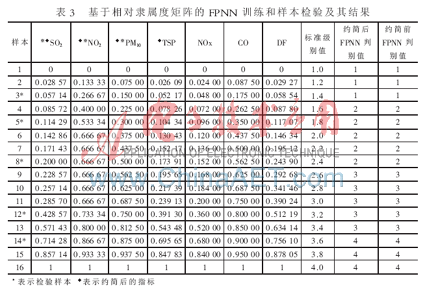
在保证相同分类结果的情况下,粗糙集理论的属性约简去掉了不相关或不重要的属性,约简后的指标为:SO2、NO2、PM10和TSP,这4个指标的值越小,表示空气受污染的程度越小,其分级标准见表2,再按2.2节所述方法,构造出标准隶属度矩阵P(篇幅有限,检测样本指标相对隶属度矩阵R略)。

根据需要,取n=5,共生成16个样本,将样本1、2、4、6、7、9、10、11、13、15、16作为训练样本,其余5个作为检验样本。SO2、NO2、PM10和TSP作为输入向量,本实验是基于Matlab7.0软件来实现整个模糊概率神经网络空气质量评价过程的,则输入层有4个神经元,径向基层的神经元个数同训练样本的个数相同,即为11个,将评价等级作为目标向量输出。本文空气质量评价共分4级,分别对应的等级值为1、2、3、4,则有4个竞争神经元;经过参数寻优运算,确定高斯函数的平滑参数为0.03~0.15之间时效果最为理想。训练结果如表3所示,可见对于训练样本和检验样本,网络的判断率都达到了100%。但指标约简后的神经网络模型结构简单,样本训练所用的时间更少。
由于影响空气质量的因素很多,导致了指标体系存在冗余,因此有必要进行指标约简。约简后的指标有:SO2、NO2、PM10和TSP,这说明目前我国空气质量主要受这四种污染物的影响,为我国有关部门合理地制定空气污染防治措施提供了依据。模糊数学理论中的相对隶属度能够表明空气质量指标的相对状态,克服了采用最大隶属度时存在的只考虑极值、容易丢失中间信息的缺陷,将它和概率神经网络相结合,建立了模糊概率神经网络模型(FPNN),该模型人为调节参数,使评价结果更客观合理,并且为了提高评价结果的质量,采用了在标准相对隶属度矩阵中进行插值的方法,生成更多的样本。仿真表明,指标约简后FPNN模型既保证了分类质量,也提高了收敛速度,实用性更强。当然本文所采用的空气质量评价方法也可以应用到其他领域中。
参考文献
[1] 史成东,陈菊红,胡健.基于粗糙集和神经网络的供应链绩效预测研究[J].计算机工程与应用,2007,43(33):203-206.
[2] 刘坤,刘贤赵.模糊概率神经网络模型在水质评价中的应用[J].水文,2007,27(1):36-39.
[3] 汪小燕.基于分辨矩阵的论域划分方法[J].电脑学习,2007(4):5-6.
[4] 李锦菊,沈亦钦.中美两国环境空气质量标准比较[J].环境监测管理与技术,2003,15(6):24-26.
[5] 飞思科技产品研发中心.神经网络理论与MATLAB 7[M].北京:电子工业出版社,2005:116-127.

