浮点反正切函数的FPGA实现-AET-电子技术应用

浮点反正切函数的FPGA实现

来源:电子技术应用2010年第8期

李全

桂林电子科技大学信息与通信学院，广西桂林541004

摘要： 设计了一种基于CORDIC算法计算浮点反正切函数的的硬件结构，并在Altera公司的FPGA芯片上进行了验证，最后在Nios II处理器系统中以用户自定义指令的形式实现，通过C语言程序验证了浮点反正切模块的正确性。

关键词： FPGA CORDIC 反正切函数浮点数据 NiosII

中图分类号： TP301
文献标识码： A

The implementation of floating arc tangent function based on FPGA

LI Quan

Information and Communication Institute，Guilin University of Electronic Technology，Guilin 541004，China

Abstract： This paper presents a architecture of arc tangent calculate circuit based on CORDIC algorithm. Software simulation and hardware experiment has been done for this module on Altera FPGA. Finally, we accomplish the hardware module by adding custom instruction on the Nios II processor system of Altera corporation. The floating-point arc tangent module′s correctness is proved by C program running in the Nios II processor.

Key words : CORDIC；arc tangent；floating-point；Nios II

    在数字信号处理、导航通讯等许多领域会大量使用反正切函数进行必要的计算，当FPGA系统应用于上述领域时常常会遇到如何使用硬件来完成反正切函数计算的问题。本文设计了基于CORDIC算法的反正切函数计算模块，并且根据IEEE-754单精度浮点数据格式对输入输出数据进行处理，实现了高精度的浮点反正切函数的计算。
1 反正切函数实现原理
   CORDIC算法有旋转模式和向量模式两种计算模式。旋转模式可以用来计算一个输入角的正弦、余弦，向量模式可以计算给定向量的角度和长度。
   CORDIC算法的基本迭代公式为：

    从上式可以看出，CORDIC算法在向量模式可以计算出给定向量(X，Y)的长度和角度，即从平面坐标到极坐标的变换。
2 数据格式转换接口模块
   本文设计的反正切函数硬件模块输入为IEEE-754单精度浮点数据，而模块内部迭代使用的是定点整型数据，因此需要进行转换。
   在图1的输入数据转换接口示意图中，X、Y为输入的IEEE-754浮点数据格式，输入范围是(－∞，＋∞)，经过接口模块转换为整型定点数据Xn、Yn，其表示范围是[-1 +1]。

矢量(X，Y)在平面坐标系中的角度为arctan(Y/X)，它只与Y和X的比值有关，与Y和X的实际长度无关。用这个性质可以以X和Y中绝对值最大的值作为归一化数值，将X和Y的范围重新映射在[-1 +1]之间，实现(X，Y)到(Xn，Yn)的转换。
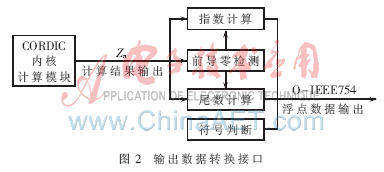
计算结束后输出结果Z。Z是32位定点整型数据，且232被定义为2π，将其规格化为IEEE-754格式的过程如图2所示。在对Z进行规格化之前，需要进行前导零检测，以确定规格化时尾数左移的位数和指数位的大小，前导零的检测硬件上可以用casex语句实现。

3 整体设计以及仿真综合
浮点反正切函数的硬件结构包括了三个主要部分，即浮点数据格式转换接口模块、CORDIC内核计算模块和浮点输出数据转换接口模块，如图3所示。

    采用Quartus II对设计进行FPGA综合，FPGA芯片选择EP2C70F896C6，硬件环境为Altera公司的DE2-70平台，总共需要1 522个逻辑单元，占用芯片资源的2%，最高工作频率为100 MHz。
4 Nios II中反正切函数的自定义指令实现
   反正切函数与Nios II CPU的接口采用multi-cycle custom instruction，dataa和datab为输入数据，result为结果输出，要从C语言中直接调用自定义指令，需要一个宏定义接口。可以在system.h文件中找到自定义指令的宏定义，如：
#define ALT_CI_CORDIC_ATAN2_N 0x00000000
#define ALT_CI_CORDIC_ATAN2(A,B) __builtin_custom_inii
(ALT_CI_CORDIC_ATAN2_N,(A),(B))
   为了正确调用自定义指令，在主程序中重新做以下宏定义：
#define ATAN2(A,B) __builtin_custom_fnff(ALT_CI_CORDIC_ATAN2_N,(A),(B))
   与system.h文件中系统自动生成的宏定义不同之处在于将宏定义的接口说明由“__builtin_custom_inii”改为了“__builtin_custom_fnff”。系统自动生成的宏定义默认输入输出皆为整型数据，改为“__builtin_custom_fnff”就是通知系统这是一条输入输出都是单精度浮点数据类型的用户自定义指令。这样由CPU调用时就不会出现数据类型不匹配的错误。
   通过在Nios II CPU中加入的JTAG_UART模块，可以从调试终端窗口中获得运行结果。硬件IP核平均计算用时73个周期，而软件计算平均用时21 000个周期，计算速度提升300倍以上。此时CPU工作频率为100 MHz，且配置为最高性能，浮点反正切函数硬件模块仅工作在50 MHz。浮点反正切函数硬件模块的计算精度完全可以满足单精度浮点数据的要求，计算误差小于10e-6，因此可以用于对精度和速度都要求很高的各种信号处理领域。
   反正切函数是应用范围最广的一个反三角函数，而用硬件实现浮点反正切函数对相应算法的速度会起到一个很大的提升作用，硬件浮点反正切函数可以很方便地作为一个IP核被系统调用，实现高速并行的超越函数计算。目前，已经设计完成并用Nios II处理器验证过浮点超越函数计算IP，包括浮点正弦函数、浮点余弦函数、浮点反正切函数和浮点反正弦函数。Nios II处理器通过加入这些IP核模块就能实现大部分浮点超越函数计算，使用硬件IP核计算比用软件计算在速度上至少可以提升300~1 000倍，这样就可以将Nios II处理器用于原先只有用DSP才能处理的一些场合，可以充分发挥FPGA系统的灵活性以及并行数据处理的能力。

参考文献
[1] Volder.The CORDIC trigonometric computing technique[J]. IRE Trans,1959：334-334.
[2] WALTHER.J.S.A unified algorithm for elementary functions[J].Spring Joint Computer Conf，1971：379-385.
[3] 李全，李晓欢，陈石平.基于CORDIC算法高精度浮点超越函数的FPGA实现.电子技术应用，2009，35(5)：166-168.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容