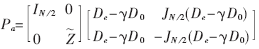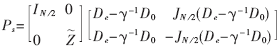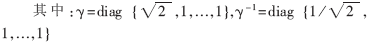一种改进的重叠变换算法在图像压缩中的应用
2008-09-16
作者:陈璐怡 邹雪妹
摘 要: 提出了一种DCT与LBT相结合的改进LBT方法,应用于图像压缩" title="图像压缩">图像压缩中。实验结果表明,它能够有效地降低块效应" title="块效应">块效应和振铃效应,使图像压缩质量有很大的提高。
关键词: 离散余弦变换" title="离散余弦变换">离散余弦变换 重叠正交变换 双正交重叠变换 块效应 振铃效应
变换编码对图像压缩是一种非常有效且常用的工具。在编码过程中,图像被分为N×N的块后,对每一块作变换,然后对变换系数进行量化和熵编码。解码是编码的逆过程,接收端从信道收到压缩图像数据后,经过解码器,恢复并重构" title="重构">重构出数字图像。
在变换编码中,尤其是在低比特率下,会产生两种典型的人工效应:块效应和振铃效应。块效应是由于连接、重构块时,块边缘处产生的信号不连续现象。振铃效应是由于变换系数中的量化噪声而产生的在整个块中蔓延的信号错误。
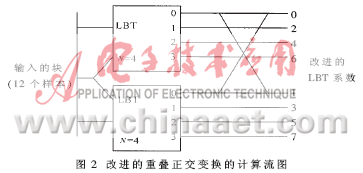
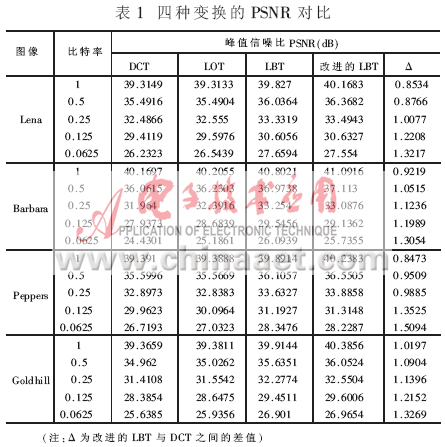
离散余弦变换(DCT)自被提出后,由于其良好的去除数据相关能力和低计算复杂性的特点,已被用于JPEG、MPEG等图像压缩和视频压缩。但比特率较低时,用DCT压缩会出现明显的块效应。为了改善低比特率时压缩图像的质量,H.S.Mavlar等提出了重叠变换。重叠变换可以有效地降低块效应。其中双重叠正交变换(LBT)比重叠正交变换(LOT)[1]降低块效应的效果更好,但却会有较明显的振铃效应。所以本文在对这几种变换研究的基础上,提出了一种改进方法。实验表明,它能够有效地降低块效应和振铃效应。
1 重叠正交变换(LOT)
将长度为MN的1D离散信号x0划分为M段,每段信号长度均为N。设传统的正交变换矩阵为T,y0为变换后的系数向量,则:
y0=TTx0
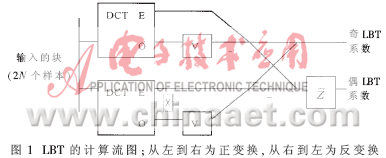
其中:T为MN×MN阶的分块对角阵;TT为T的转置矩阵。与传统的正交变换类似,LOT将信号划分为M段,但每段长度L满足N 其中:P0为L×N阶矩阵。由于信号的起始和末尾两段只有一端信号重叠,因此需要分别定义P1和P2。由于P0不是方阵,因此,P0是不可逆的。但对于整体变换矩阵T,要求其具有可逆性和正交性。为保证T正交,要求P0的每一列必须是正交的,即: P0TP0=I 同时,相邻两段的重叠函数必须也满足正交性,即: P0TWP0=P0WP0T=0 其中:转移矩阵W为: 上式中I为L-N阶单位矩阵。一般选取L=2N, 与传统正交变换完全类似,2D信号的LOT可由1D信号的LOT直接导出。从DCT可以得出一个可行的LOT变换矩阵[1]: 其中:De是由N阶DCT矩阵的偶数行(i=0,2,...,N-2)向量组成的N/2×N阶矩阵;D0是由N阶DCT矩阵的奇数行(i=1,3,...,N-1)向量组成的N/2×N阶矩阵; 2 双正交重叠变换(LBT) LOT在图像变换编码中能够有效地减少块效应。但在大多数情况下,一些残留人工效应仍然可见,因为其基函数在边缘处没有衰减到0。一种使LOT能够在边缘处衰减到0 的方法是使用双正交重叠变换(LBT)。在双正交重叠变换里,2N×N的正反变换矩阵Pa和Ps不满足正交条件,但它们在一起时仍然满足正交和重叠正交的条件PaTPS=I和PaTWPS=0。当Pa=Ps时,可以说LBT就是LOT。LBT的正变换是将第一个" title="第一个">第一个奇对称的DCT系数乘 反变换矩阵为: 图1是LBT 的计算流图。 3 对双正交重叠变换的改进 由于LBT的基函数太长(L=2N),它产生的振铃效应与LOT差不多,所以本文针对这一不足提出了一种对LBT进行改进的计算方法——LB-DCT:对于一个给定大小为N=8的块,进行分层变换,在第一层里,对N/2大小的块进行LBT变换,可降低块效应;第二层里,再对大小为N的块进行DCT变换,可使基函数长度减小从而降低振铃效应。这种分层变换的低频函数(DC和第一个AC)的长度是1.5N=12(LBT和LOT的长度是2N=16),即相邻两块之间有33%的部分重叠,而LBT和LOT是50%。高频函数的长度与DCT基函数的长度相同,都等于块大小N=8。然而,由于它的边缘能够平滑地衰减到0,函数的有效长度比块的长度短,所以它产生的振铃效应比DCT、LOT、LBT少。这种变换的计算流图如图2所示。 从图2可以看出:这种变换的计算复杂度比LOT和LBT低,对于每个子块需要16个乘法和42个加法;而LOT需要22个乘法和54个加法;LBT需要23个乘法和54个加法(DCT需要13个乘法和29个加法)[3]。 4 实验结果 以4幅标准的512×512的8bit灰度测试图像为实例,用C语言实现了一个检验各种变换压缩性能的测试平台,分别对四种变换的压缩性能进行了测试。以峰值信噪比(PSNR)为评价标准,表1列出了四种变换的PSNR对比。可以看出,尽管改进的LBT的计算复杂度比DCT提高了30%左右(LOT和LBT比DCT复杂度提高了80%),但是其PSNR值却提高很多,且比特率越低差距越明显。 DCT变换在低码率下会产生较明显的块效应,重叠正交变换(LOT)和双重叠正交变换(LBT)在图像变换编码中能有效地减少块效应,且后者相对于前者,去除块效应的性能较好,但产生的振铃效应仍然较多。本文在对上述技术深入研究的基础上,采用DCT与LBT相结合的方法,对LBT进行了改进。实验证明,这种改进的LBT与DCT相比不仅能够获得更高的编码增益,而且由于其光滑的低频函数和较短的高频函数使得块效应和振铃效应也比DCT、LOT、LBT低,使图像压缩质量得到较大的提高。 参考文献 1 H.S.Malvar, D.H.Staelin.The LOT:Transform coding without blocking effects. IEEE Trans. Acoustics, Speech and Signal Processing. 1989;37(4):553-559 2 Hong Man, Ricardo de Queiroz , Mark J. T. Smith.3-D Subband coding techniques for wireless video communications. IEEE Trans. on Circuits and Systems for Video Technology, 2002 3 钟广军,成礼智,陈火旺. 双重叠正交变换的整数实现算法与图像压缩. 电子学报, 2001;29(11):22-24 4 Toshihisa Tanaka , Yukihiko Yamashita. A Biorthogonal Transform with Overlapping and Non-overlapping Basis Functions for Image Coding.IEEE Trans. Signal Processing. 2002 5 Trac D.Tran, Jie Liang , Chengjie Tu. Lapped Transform via Time-Domain Pre-and Post-Filtering. IEEE Trans.on signal processing,2003;51(6):1557-1569 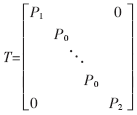
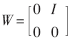
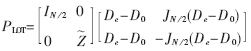
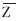 为待定的、可获得较高编码增益的N/2阶正交矩阵;IN/2为N/2阶的单位矩阵,JN/2为N/2阶的倒序矩阵。
为待定的、可获得较高编码增益的N/2阶正交矩阵;IN/2为N/2阶的单位矩阵,JN/2为N/2阶的倒序矩阵。  从而得到LBT的正变换矩阵[2-3]:
从而得到LBT的正变换矩阵[2-3]: