在工业生产中,常需要采用闭环控制方式来控制温度、压力、流量等连续变化的模拟量。无论是使用模拟控制器的模拟控制系统,还是使用计算机的数字控制系统,PID控制器都得到了广泛的应用。这是因为这种方法不需要精确的控制系统数学模型,有较强的灵活性和适应性。但是在数字PLC控制系统中,普通的 PID算法对所有过去状态存在依赖性,从而引起系统较大的超调,使系统稳定性下降。增量式PID控制算法" title="控制算法">控制算法每次输出只输出控制增量,必要时可通过逻辑判断限制故障时的输出,从而降低了因机器故障导致PID误输出给系统带来严重后果的影响。
在实际系统中,PLC控制模拟量可采用PLC自带的PID过程控制模块,但对要求比较高的场合采用改进的PID控制算法,就必须由用户自己编制PID控制算法,基于这些问题的考虑,文中介绍一种由三菱FX2N实现的增量式PID控制器的设计方法。
1 控制原理
1.1 PID控制原理
PLC的PID控制器的设计是以连续系统的PID控制规律为基础,将其数字化,写成离散形式的PID控制方程,再根据离散方程进行控制程序设计。
在连续系统中,典型的PID闭环控制系统如图1所示,图中sp(t)是给定值,pv(t)为反馈量,c(t)为系统的输出量。
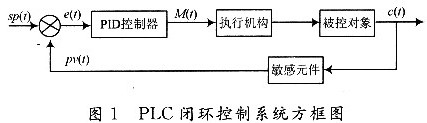
PID控制器的输入/输出关系式为:

式中:M(t)为控制器的输出;M0为输出的初始值;e(t)=sp(t)-pv(t)为误差信号;Kc为比例系数;T1为积分时间常数" title="时间常数">时间常数;TD为微分时间常数。
式(1)中等号右边前3项分别是比例、积分、微分部分,他们分别与误差、误差的积分和微分成正比。假设采样周期" title="采样周期">采样周期为Ts,系统开始运行的时刻为t=0,用矩形积分来近似精确积分,用差分近似精确微分,将式(1)离散化,第n次采样时控制器的输出为:
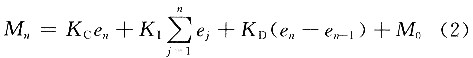
式中:en-1为第n-1次采样时的误差值;K1为积分系数;KD为微分系数。
由式(2)可知,控制器输出的第二项是误差积累的结果,会使得超调量过大,而这些在有些工业过程中是不允许的。所以常规PID控制算法很难控制这类过程。
1.2 增量式PID控制规律
增量式PID的结构框图如图2所示:
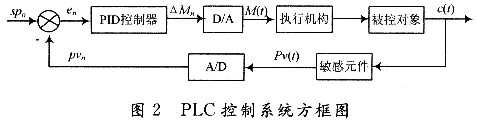
由式(2)的表达式,就可以根据“递推原理”得到Mn-1的表达式:

式中:A=KC+KI+KD;B=KC+2KD;C=KD。A,B,C都是与采样周期、比例系数、积分时间常数、微分时间常数有关的常数。
由式(4)可知,增量式PID算法建立在对普通PID算法进行改进的基础之上。它克服了位置式PID对所有过去状态的依赖,计算机控制器输出的只是增量,所以误动作的时候对输出的影响比较小,必要的时候可以使用逻辑判断的方法将这种影响消除,因而不会严重影响系统的工况。由于算式中不需要对误差进行累加,控制增量△Mn的确定仅与最近的n,n-1,n-2次的采样值有关,较容易的通过加权处理而获得比较好的控制效果。
2 PLC软件设计
2.1 程序流程
图3给出了增量式PID控制算法的程序流程框图。在进行初始化时,应根据系统性能要求选定参数KC,KI,KD和采样时间TS,从而确定系数A,B,C,并设置偏差初值en-1=en-2=0。
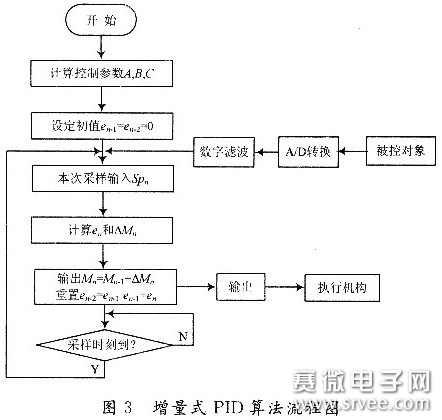
2.2 控制算法的参数确定
参数整定" title="参数整定">参数整定是控制系统设计的核心内容。它是根据被控过程的特性确定PID控器的比例系数、积分时间和微分时间的大小,以改善系统的动态特性和静态特性,取得最佳控制效果。本文采用临界比例度法。假设选取的控制度为1.05,根据经验选取临界比例度Kr=20%,临界振荡周期Tr=60 s,得参数整定初始值TS=O.90 s,KC=O.126,TI=30 s,TD=8 s。
基于三菱FX2NPLC的部分程序如下:

3 结语
该文在分析普通PID控制算法的基础上,提出了增量式PID算法的控制原理" title="控制原理">控制原理,通过了自编程序在三菱FX2NPLC上实现了改进的PID算法。由实际模型的验证结果表明,此方法可以有效地减少系统的超调量,使其得到更好的控制效果,因此在实际的工程应用中具有较好的借鉴作用。

