摘   要： 针对模糊c-均值（FCM）聚类算法受初始聚类中心影响，易陷入局部最优，以及算法对孤立点数据敏感的问题，提出了解决方案：采用快速减法聚类算法初始化聚类中心，为每个样本点赋予一个定量的权值，用来区分不同的样本点对最终的聚类结果的不同作用，为提高聚类速度采用修正隶属度矩阵的方法，并将算法与传统的FCM相比。实验结果表明，该算法较好地解决了初值问题，与随机初始化方法相比，迭代次数少、收敛速度快、具有较好的聚类结果。
关键词： 模糊c-均值； 减法聚类； 权值

    模糊聚类作为无监督机器学习的主要技术之一，广泛应用于数据挖掘、矢量量化、图像分割、模式识别、医学诊断等领域。引入模糊数学方法,通过建立数据样本类属的不确定描述,将相似性质的事物分开并加以分类，能比较客观地反映现实世界。
    模糊c-均值（FCM）算法是模糊聚类的基本方法之一，它是一种聚类不定归属的方法。它通过引入隶属度函数来表示每个样本点属于各个类别的程度，从而决定样本点的类属,对数据进行软划分。
    FCM算法就是通过搜索目标函数的最小点，反复修改聚类中心矩阵和隶属度矩阵的分类过程。目前算法的收敛性已得到证明[1]，但它是一种局部搜索算法，对初值的选取十分敏感，如果初值选取不当，它容易收敛到局部极小点。且FCM对孤立点数据、样本分布不均衡也很敏感。鉴于此，提出基于减法聚类的改进的模糊c-均值聚类，使得算法的收敛速度和准确性都得以改善。
1 模糊c-均值算法分析


2 基于减法聚类的改进的模糊c-均值算法
2．1初始聚类中心的选择
    减法聚类是一种爬山法，它把所有的样本点作为聚类中心的候选点，其基本思想是计算每个样本点的密度指标，如果该样本点周围的点多，则密度指标就大，就选取密度指标最大的样本点作为聚类中心。减法聚类是一种快速独立的近似的聚类方法，用它计算，计算量由样本数目决定且与样本点的数目成简单的线性关系，而且与所考虑问题的维数无关。


    (2) 修正隶属度矩阵
    FCM算法的思想是：迭代调整隶属矩阵和聚类中心使目标函数值最小,为保证FCM算法每次的迭代都朝着全局最优的方向逼近，其关键就在于保证确定V的下一次迭代值，加快收敛于全局最优点的速度。在此采用修正隶属矩阵来计算下一次迭代的聚类中心，使得到的V更靠近聚类中心，更合理，从而提高FCM算法的收敛速度。因此修正隶属度矩阵[5]可以提高聚类速度，使聚类效果更好。
    样本离聚类中心距离越远属于该聚类中心的程度越小，反之越大，样本对类中心的影响即称为样本对类中心施加的吸引力，在这里设定了一个抑制因子，由它来控制对离样本点次最近的类中心的抑制作用。
    当α＝１时，算法退化为FCM算法，对离样本点次最近的类中心没有任何抑制作用。
    当α=0时，算法完全抑制了样本对离它次最近类中心的吸引力，对离样本最近类中心的吸引力的增强力度最大。
    当1<α<0时，算法对离样本次最近类中心的吸引力有一定的抑制作用，对离样本最近类中心的吸引力有一定的增加作用。
    修正隶属度矩阵的过程如下：
  
    (5) 判断是否终止迭代。终止而退出，否则，L=L+1，返回步骤(２)，继续迭代。
    经过对隶属度矩阵的修正可知：改进后的算法，样本点增大了对离它最近的类中心的吸引力强度；样本点减小了对离它次最近的类中心的吸引力强度，从而减弱了离样本次最近类中心对离样本最近的类中心收敛速度的延缓作用。对其余类中心的吸引力强度不变，从而提升了FCM算法的收敛速度。
2．3 基于减法聚类改进的模糊c-均值算法过程
    为保证改进的FCM聚类结果为全局最优解，采用减法聚类的聚类中心作为改进的FCM聚类的初始聚类中心。算法步骤如下：
    (1) 设定聚类参数:领域的半径ra、rb,比例参数δ，FCM聚类数c,模糊指数m和最小误差ε,迭代次数L,吸引力抑制因子α。
    (2) 应用式(4)计算所有样本点的密度指标，将密度指标最高的一个作为第一个聚类中心点xc1。
    (3) 依据公式(5)利用减法步骤(2)中的xc1进一步计算余下的n-1个数据点的密度指标，找出最高的作为第二个聚类中心xc2，依此类推，找到p个聚类中心，从中选取前c个作为FCM的初始聚类中心v(0)。
    减法聚类中心中，密度指标越大的聚类中心出现得越早，越有可能成为改进的FCM初始聚类中心。所以，当聚类数为c时，取减法聚类产生的前c个聚类中心作为改进的FCM的初始中心，无须再重新初始化，从而提高了聚类的效率。
    (4) 求式(10)的最小值
    (5) 按式(11)和式(12)计算出隶属度U(L)
    (6) 依据式(13)和式(14)修正隶属度矩阵U(L)。
    (7) 依据式(15)，用修正后的U(L)计算下一次的迭代中心V(L+1)。
    (8) 判断是否满足终止迭代条件。对给定的阈值，
‖U(L+1)-U(L)‖<ε如果终止而退出，否则，L=L+1，返回步骤(5)，继续迭代。
3 仿真与结果分析

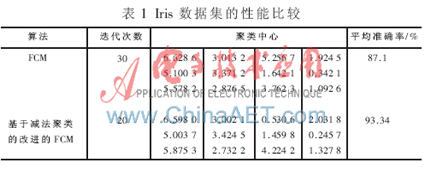
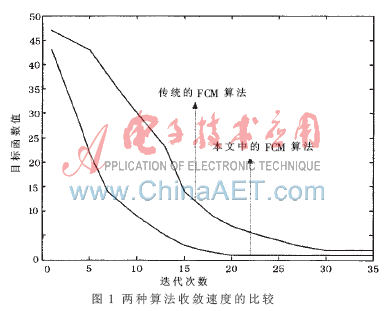
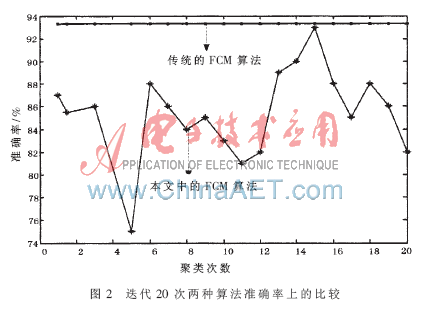
    从图1、图2与表1中可以看出,传统FCM与本文中的算法相比迭代次数少、搜索速度更快、聚类平均准确率更高。

    基于减法聚类的改进的FCM算法很好地解决了FCM算法对初始值敏感及易陷入局部最优的问题，同时也改善了FCM对孤立点敏感的问题，提高了聚类的速度，具有很高的实用价值。
参考文献
[1]  GAMES R A, CHAN A H. A fast algorithm for determining the linear complexity of a pseudorandom sequence with period 2n[J].IEEE Trans Inf Theory ,1983,IT-29(1):144-146.
[2]  HAND D, MANNILA H, SMYTH P. Principles of data mining [M].Cambridge MA:MITPress,2001.
[3]  PAL N R, CHAKRABORTY D. Mountain and subtractive clustering method; Improvements and Generalization. International Journal of Intelligent Systems , 2000,15 (4):329-341.
[4]  齐淼，张化祥.改进的模糊c-均值聚类算法研究[J].计算机工程与应用,2009,45(20).
[5]  闫兆振.自适应模糊c-均值聚类算法研究[D]. 济南：山东科技大学,2006.