引言

　　Reed-Solomon码首先是由Reed和Solomon两人于1960年提出来的，简称为RS码。这是一类具有很强纠错能力的多进制BCH码，既能纠正随机错误，也能纠正突发错误，也是一类典型的代数几何码。RS码一直以来都是国际通信领域研究的热点之一。

　　本文以战术军用通信系统的首选码RS(31，15)码为例，对生成多项式进行了优化，并采用查表法的原理极大地提高了编码器运算数据的能力，缩短了运算周期，最终利用VHDL语言编译，在FPGA" title="FPGA">FPGA中实现，得到了正确的RS编译码。

　　1 RS编码原理

　　能纠正t个错误的RS(n，k)码具有如下特性：

　　码长：n=2m-1符号或m(2m-1)比特;信息码元数：k=n-2t符号或mk比特;监督码元数：n-k=2t符号或m(n-k)比特;最小距离：d=2t+1=n-k-1符号或m(n-k+1)比特;最小距离为d的本原RS码的生成多项式一般为：

　　令信息元多项式为：

　　监督多项式为：

　　则码多项式为：

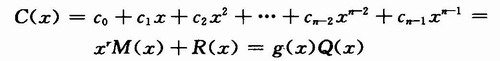
　　式中：Q(x)是g(x)整除C(x)所得的商式。所有这些原理都与二进制循环码一样，不同的仅在于运算方法。对于二进制码，码多项式各项系数只能取0或1，多项式的加减乘除是模二运算，是定义在GF(2)域上的多项式。现在码多项式各项系数可以取q=2m种不同的值，应当是定义在GF(2m)域上的多项式。

　　2 生成多项式的优化

　　以RS(31，15)为例，n=31，k=15，可纠正错误数为t=(n-k)/2=8;以

为本原多项式，可得到GF(25)上的元素如表1所示。

　　一般的生成多项式为：

　　则码字多项式以

为零点。

　　由于注意到：

　　3 RS编码器" title="RS编码器">RS编码器的设计

　　在GF(2m)域上的加法运算实际上就是每位作异或运算，由异或门组合而成即可。

　　由于优化了生成多项式g(x)，这里只需要在ROM中存入

的乘法表即可。

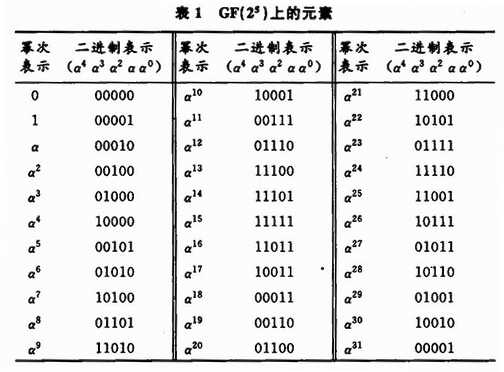
　　由加法模块和乘法模块组成的一级模二运算电路如图1所示。

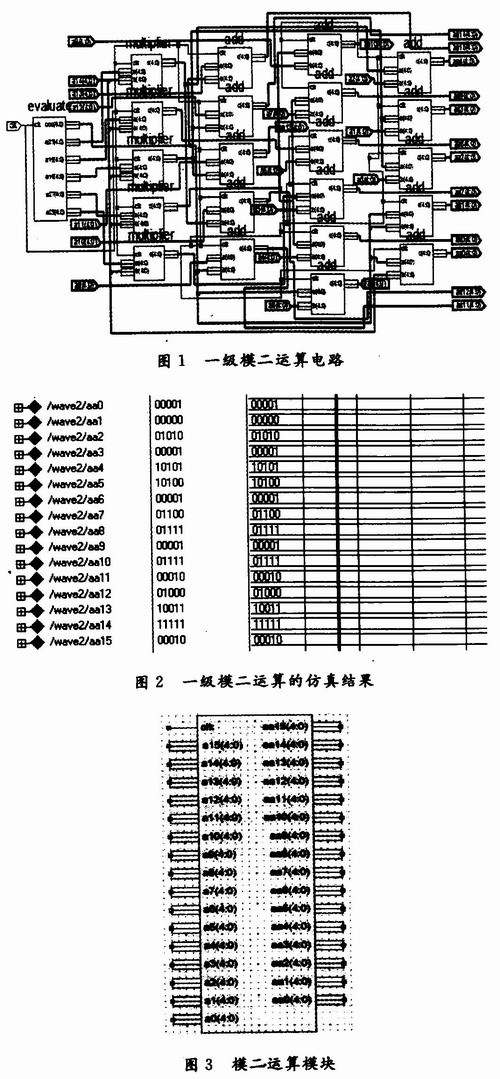
　　利用ISE9.0仿真软件得到的运算一级模二运算的仿真图如图2所示。

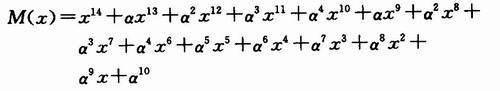
　　生成的一级模二运算模块如图3所示。

　　依次连接多个模二运算模块，进行一步步模二运算，得到余数多项式的系数，即为RS校验码。图4为当信息码字为M时的RS编译结果。

　　可看到此时：

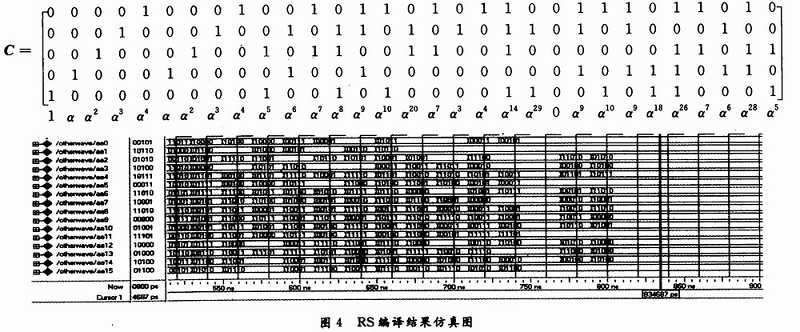
　　4 FPGA实现

　　通过RS编码后的数据为5×31的矩阵，形如;

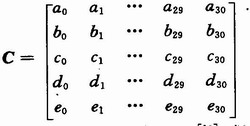
　　将5行数据交织编码，交织度为I=5，得到(ao bo co do eo a1 b1 c1 d1 e1…a30 b30 c30 d30 e30)的形式，利用示波器从串口读出，得到波形图如图5所示。

　　5 结语

　　给出的RS编码器设计方法对生成多项式进行了优化，使得ROM中需要存入的乘法表大幅减少，模拟模二运算的步骤设计编码过程，最终烧入FPGA中，利用示波器采集到了正确的数据，证明RS编码器编码正确。本文介绍的RS编码器设计方法简单，占用资源少。