0 引言
    模数转换器(ADC)在信号处理中起了一个非常重要的作用。在数字音频、数字电视、图像编码及频率合成等领域需要大量的数据转换器。由于超大规模集成电路的尺寸和偏压不断减小，模拟器件的精度和动态范围也不断降低，对于实现高分辨率的ADC是一种挑战。高阶多位Delta-sigma ADC由于不需要采样保持电路，电路规模小，可以实现较高的分辨率，因此在实际中得到广泛的应用。Delta-sigma ADC采用过采样技术和噪声整形技术相结合，对量化噪声双重抑制，从而实现高精度模数转换。在实际的设计中需要根据设计指标稳定性和动态范围等进行折衷。要实现大的动态范围，就需要较高的过采样率和多位量化器。为了保持高阶DSM的稳定性就需要使用多位量化器，而多位量化器会增加后续内部ADC的设计难度。因此，必须仔细选择过采样率和量化器的位数，以实现预期的性能指标。本文提出一种三阶单环局部反馈的Delta-sigma调制器结构，利用Richard Schreier的Matlab Delta-sigma调制器设计工具包，推导调制器传输函数，并对系数进行优化，使用Verilog硬件语言对调制器进行行为级建模。调制器的信号带宽为32．8kHz，过采样率为128，工作时钟8．4MHZ，精度16位，可以达到145dB以上的SNR。

1 Delta-sigma调制器的原理和结构
    △-∑调制技术来自高分辨率的A／D、D／A变换器中的过取样△-∑转换技术，利用经典自动控制理论中负反馈概念，通过反馈环来提高量化器的有效分辨率并整形其量化噪声。在对信号进行过取样后，噪声功率谱幅度降低，并通过一个对输入呈低通而对量化噪声呈现高通的噪声整形器，将量化噪声功率的绝大部分移到信号频带之外，从而可通过滤波有效地抑制噪声。
    Delta-sigma调制器的仿真模型可以用图1来表示。该系统是一个双端输入、单端输出的线性系统，系统的一个输入为外部输入信号U，另一个输入为量化器的反馈V，输出则是量化器的输入Y。

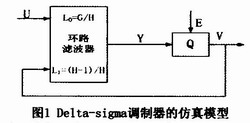
    由图1根据叠加原理，可知系统的输出可以表示为
   
其中，L0(z)和L1(z)分别是输入U(z)和V(z)到输出Y(z)的传递函数。
    令调制器量化噪声为E(z)，则调制器的输出为
   
由式（1）、（2）可得
   
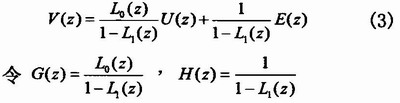
其中G(z)是信号传递函数(STF)，H(z)是NTF(NTF)。所以
   
    这种仿真模型将不同结构的Delta-sigma调制器用同一种模型来描述。因此，在设计调制器的NTF时不必考虑调制器具体的实现结构。

2 三阶单环DSM结构
2．1 高阶稳定的调制器函数的设计
    高阶Delta-sigma的NTF具有一般形式(5)。从表达式可以看出，NTF的n个零点都集中直流频率处。但是，文献指出，如果将NTF的零点均匀地分布在信号基带中，而不是全都集中在直流频率处，将对量化噪声有更好的整形效果。Delta-sigma调制器的不稳定状态主要与调制器N-TF的带外增益有关，为了限制NTF的带外增益，将式(5)所示的NTF的一般表达式改写成式(6)。
   
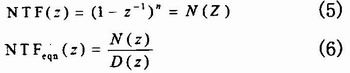
    通过调整D(z)就可以有效地达到限制NTF带外增益的目的。
    Delta-sigma调制器的设计重点就是设计出使系统稳定mSTF和NTF。。在文献中指出，NTF的极点决定了它的带外增益，而带外增益又与系统的噪声整形性能及稳定性密切相关，带外增益越高，噪声整形的效果越好，但是带外增益过高系统将不能稳定，而且带外增益越高则输入信号的稳定的范围越小。所以，对于3阶以上的Delta-sigma调制器，随着输入信号幅度的增加，调制器的SNR线性增长，但是当输入的幅度超过一定值后。调制器的SNR突然下降，这时的调制器就处于不稳定的状态。NTF的带外增益决定了输入信号幅度和调制器输出SNR之间的一对矛盾关系。
    在调制器阶数、过采样率以及调制器位数确定的情况下，调制器NTF设计的关键问题是，找出调制器能够稳定所对应的输入范围。最大SNR所对应的输入范围就是调制器能够稳定所对应的输入范围。
2．2 改进的DSM结构图
    实现传输函数的拓扑结构不是唯一的，是多种形式的，一般来说有四种结构使用最为普遍CIFB(cascade-integrator-feedback)、CRFB(cascade-resonator-feedback)、CIFF(cascade-integrator-feedforward)、CRFF(cascade-resonator-feedforward)。如果不需要经过零点优化，可以采用CIFB和CIFF的结构，需要零点经过优化可采用CRFB和CRFF结构。本文是高精度调制器的设计，而经过零点优化的可以得到更好的噪声整形，实现更高的精度，而CRFF相对CRFB结构在电路设计方面具有结构更为简单和电路规模更小的优势，所以采用CRFF结构，如图2。

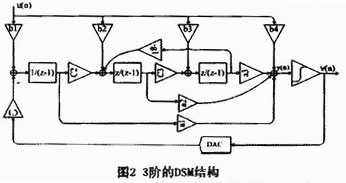
    由图可以看出，输入信号在比较器前与前馈信号直接相加，实现了STF为1，因此数字滤波器可以不需要考虑基带补偿；al-a3前馈方式实现NTF的极点，降低了积分器输出的幅度；第三级积分器输出通过g反馈给第二级积分器，即局部反馈(LFB)，这在NTF中引入了共轭零点，挺高了基带SNR。根据高阶稳定的调制器函数的设计方法，设计一个过采样率为128和3位量化器的3阶调制器，图2中的系数值(a1、a2、a3、a4、bl、b2、b3、b4、cl、c2、c3、g1)，由Richard Schreier提供的Matlab Delta-sigma调制器设计工具包可以得出，具体值在表1中给出，表中的数值用于设计NTF和STF的Matlab模型。在实际的数字电路实现时，为了减少芯片面积和设计难度避免使用乘法器，所以这些系数均取2n的近似值，这样可以用移位相加来代替乘法。利用Richard Schreier提供的Matlab Delta-sigma调制器设计工具包得到带外增益为6.1，DSM的NTF为
   

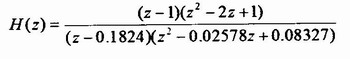
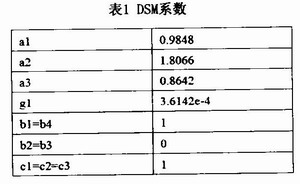
2．3 Verilog语言行为级建模
    图2所示的是一种单路差异积分器调制器，可用延迟积分器和非延迟积分器，以及各种前馈和反馈路径组合而成。在Matlab结构中对应的积分器转换成Verilog硬件描述框图的过程如图3所示

    本文使用Verilog硬件语言来实现单回路差异积分调制器，由时钟控制构成延迟积分器与非延迟积分器的相加动作。assign指令使等式两边永远处于活动状态，而alwavs指令将会在时钟正好触发时将sum的值存入寄存器delay_sum中，因此，所有的积分器将会在每一次时钟完成时完成一次累加动作。同理，非延迟积分器是由相同的程序代码组成。实现延迟积分器的程序部分代码如下表示：


3 模型的仿真结果
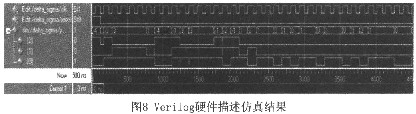
    图3给出的是NTF的极点与零点图。很明显，NTF的零点均匀地分布在信号基带中，而不是集中在直流频率处。图4给出了输入幅度范围与SNR。图5给出了NTF和STF的幅频响应。可以看到，带内信号的衰减几乎是0，而图6显示噪声的衰减小于-110dB，满足带内噪声的要求。图7给出了调制器的频域特性图。图8给出的是在输入为42000，时钟频率为8．4MHz的verilog硬件描述语言的仿真结果，可以看出经过2μs后结果趋于稳定。

4 结论
    本文提出一个用在ADC中的16位的3阶8级量化的三阶单环Delta-sigma调制器。为了提高电路性能，实现较高的SNR和DR，减少量化噪声的影响，在设计NTF时采用前馈方式和局部反馈的结构，并进行零点优化，通过这些方法优化了输出SNR，提高DR，降低量化噪声，使得电路对于量化噪声有较好的敏感度。根据仿真结果，这个DSM的峰值SNR可以达到145dB以上，在3阶的系统和128的过采样率下，达到相当高的SNR，之后用Verilog语言对调制器各电路模块进行建模与仿真。