高性能滤波器是现代信号处理的一种基本电路，传统的设计思想和方法运算量大，实现困难。在信号处理的各种应用中，电子线路的输入信号都含有各种频率分量，其包含的分量有有用信号和干扰信号。对于无用的信号需将其滤除或尽量地抑制到最低，这种对无用频率分量加以滤除或抑制的电路就是滤波器。Chebyshev有源滤波器有特定的中心频率信号，抑制和滤除其它频段的信号，在各种电子电路、自动控制电路中应用广泛。
    利用OrCAD／Pspice将电路原理图绘制完成就可以使用实现电路的仿真分析。在电路的分析和优化设计中，可以随时调整电路结构，再次进行模拟分析，最终达到设计要求。其中Probe模块，可以在模拟结束后显示结果信号波形。而且，还可以对波形进行各种运算处理，包括提取电路特性参数，分析电路特性参数和最大增益分布直方图。它可以对电路进行高性能的分析，是模拟电路分析的高级形式，可以对模拟结果再分析处理，以提取更多的信息。文中设计也应用了此模块，进行了Monte Carlo分析。

1 一阶低通滤波器
    一阶低通滤波器由RC电路和放大器组成，电路原理，如图1所示。系统函数为
   
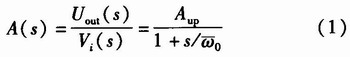
式(1)ω0=2πf0=1／R3C1中为特征频率，Aup=1+R1／R2为通带电压增益，取电源电压V-=-15 V，V+=15 V。画出一阶低通滤波器的幅频特性，如图2所示。

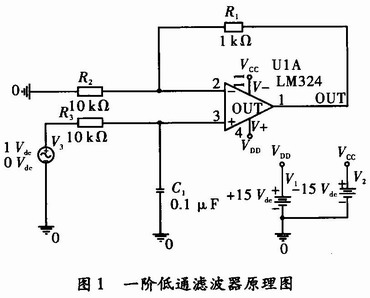
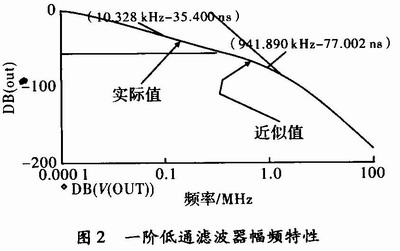
    由图2可知，当归一化频率f0≥940 kHz时，幅频特性的斜率为20 dB／10倍频，衰减的速度比较快，与理想的矩形幅频特性相差较远，过渡带较宽，如果有通带外信号，其衰减速度比较慢。故一阶低通滤波器只能用于性能要求不高的场合，若要求特性下降斜率大，对通带外信号衰减速度快，则只能应用二阶或者更高阶的滤波器电路。

2 二阶低通滤波器
    二阶低通滤波器由两个RC和放大电路组成，电路原理，如图3所示。采用正反馈技术将f0点附近的电压增益值提高，形成压控电源低通滤波器。压控电压源电路具有高输入阻抗、低输出阻抗的特点，对运放特性的理想程度要求比较低，如图3所示。

       
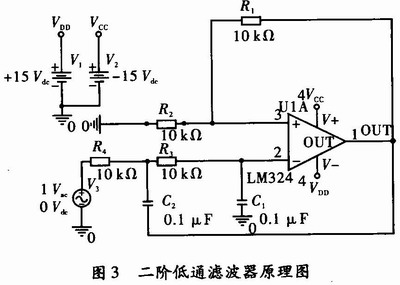
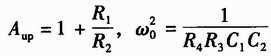
当R4=R3，C1=C2时，电路的品质因数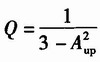，二阶低通滤波器系统的传输函数为
   
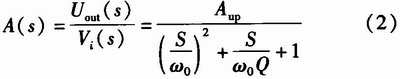
式(2)中，令s=jω，可以计算出频率特性表达式
   
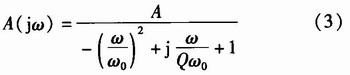
进而计算出幅频特性函数。根据图3中参数选取值可以计算出f0=159 Hz，计算滤波器最高幅频下降3 dB所对应的频率即为通带截止频率fs约为1．577 6 kHz，如图4所示。

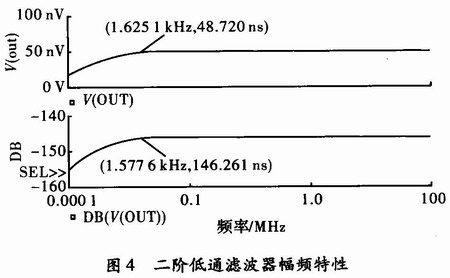
    由图4可知，幅频特性在f=1．5 kHz附近得到了提升，提升后的电路发生振荡进而可能性不稳定。为了可以使f=f0附近接近理想的水平线，幅频特性曲线下降速率约为40 dB／10倍频，速度为一阶滤波电路的2倍。这些方面，二阶低通滤波器能够满足，但仍然不是最佳的选择。波特图的变化范围比较低，由图4可知其相应的变化范围-146～-158 dB，幅频变化特性幅度变化相当低，对于更高的要求像衰减速度快、稳定性能好等还是需要更阶有源滤波器来实现。如4阶Chebyshev有源滤波器。

3 四阶Chebyshey有源滤波器
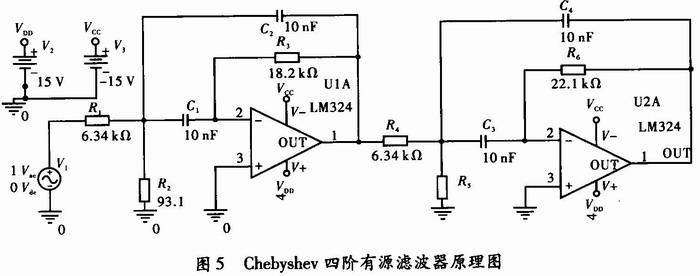
    4阶Chebyshev有源滤波器由4个电容、6个电阻和2个放大器组成，应用一阶、二阶低通滤波器同样的分析方法对其分析。4阶Chebyshev有源滤波器的截止频率在很宽的范围内可以调节，对通带外信号衰减速度快、带通滤波器的带宽较宽。其相应的反馈电路，提高了静态工作点的稳定性，下面说明分析4阶Chebyshev有源滤波器特性，电路原理，如图5所示。

    由图6，图7可知，幅频特性中心频率为10 kHz，带宽为1．5 kHz，波特图变化范围从-58～0 dB，与二阶低通滤波器相比具有二阶不能具有的优良特性，如相频特性好、稳定性能高等。

    Monte Carlo分析是在给定电路元件参数的统计分布规律的情况下，用一组伪随机数求的元件参数的随机抽样，估算出电路性能的统计规律。进行MonteCarlo分析时，根据实际情况确定元器件值分布规律，多次“重复”进行指定的电路特性分析，每次分析时采用的元器件值是从元器件值分布中随机抽样，每次分析时采用的元器件值完全相同，而是代表实际变化情况。多次电路特性分析后，对各次分析结果进行综合统计分析。Monte Carlo分析是一种随机抽样、统计分析的方法，简称MC分析。MC分析结束后，采用波形显示分析模块Probe可以用直方图表示电路特性的分散情况。再与规范值相比较，就可以得到满足规范要求的电路所占的比例，这也就是成品率，因此MC分析又称为成品率分析。
    如图5 Chebyshev 4阶有源滤波器，如果投入生产时要求组装100套滤波器，所有电阻采用精度为1％的电阻器，所有电容采用精度为5％的电容器，应用Probe模块的命令系统，对电阻进行蒙特卡洛(Monte Carlo)分析，绘出更直观的直方图。
    对考虑其值发生随机变化的元器件应采用Breakout库中的符号，编号和阻值不变，设置电阻、电容的模型参数变化。比如R1和C1的模型分别描述为。
    MODEL Rbreak RES R=6．34 k DEV=1％
    MODEL Cbreak CAP C=6．34 k DEV=5％
MC分析的参数设置之后，进行MC分析和结果显示，应用Performance Analysis功能绘出MC最大增益波形图和最大增益分布直方图分别，如图8和图9所示。

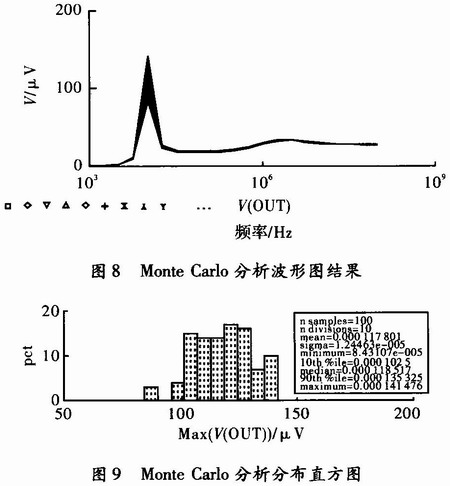
    显然从图8可以看出，Chebyshev 4阶有源滤波器通过采用随机抽样、统计分析方法的MC和Pspice仿真分析的结果几乎完全相同。输出幅频特性的中心频率约10 kHz，带宽达到1．5 kHz，进而也再次认定了Chebyshev 4阶有源滤波器具有良好的幅频特性、较高的稳定性和提高了带宽。图9可以看出，直方图显示了最大增益在不同范围内的Chebyshev 4阶有源滤波器电路所占的比例。同时在直方图的下方还显示了直方图有关信息说明和统计分析结果。

4 结束语
    用Pspice软件分析低通滤波器，以直接可视化的结果反映的幅频特性，避免了复杂运算。经过比较低通滤波器的功能，设计出4阶Cheby-shev有源滤波器，并仿真出直观的频率特性。运用Probe模块，对4阶有源滤波器模拟结果的再高级分析处理。另外，如果有特定要求的电阻电容精度，如果投入生产组装大量4阶Chebyshev有源滤波器时，采用随机抽样、统计分析的MC方法，确定Chebyshev 4阶有源滤波器的特性，其大量生产时仍具有高稳定性，为大量生产明确了目标性能。