随着当今工业生产的不断发展,在特种金属热处理的工艺要求中,具有超调响应的PID(Proportional Integral Derivative)温控系统已不能满足特殊生产的需求,它不仅需要在加热过程中严格执行预定的温升曲线,而且尤其注重温度拐点的工艺控制,必须做到既无欠温而又无过温的控制效果。欠温时达不到预定的工艺要求,而过温可能会造成加热工件的晶粒组织形成永久性的破坏而导致产生废品。在金属加热温度控制系统中,由于加热源与被加热对象之间控制惰性的客观存在,在系统噪声、负载扰动等时变不确定性的影响下,若要求加热工艺过程实时准确执行预定温度曲线,采用典型的PID控制思路是难以实现的。在以往的生产过程中,为防止超调过烧,在温度的拐点处是以欠温状态为代价运行的,为追求产品的高质量水平,经反复探索、研究、实践,在应用Siemens Smatic S7-200 PLC的PID指令的基础上,通过实践新型PID自适应控制理论,对不同温度段PID各参数的适时变更、调节,突破了欠温与超调相互制约的矛盾,达到了与系统预定的升温曲线相一致的控制结果。
1 系统组成简介
系统设备的基本组成如图l(a)所示,具体控制过程为:在工控机组态软件的支持下,通过人机界面的交互输入或修改预定的工件加热温升曲线,系统的人机界面如图l(b)所示,生产过程的操作均通过人机界面上相应指示实施。设备运行后,PLC将依照组态预定的温升曲线,对变频电源的功率输出进行实时PID调节,从而控制感应加热设备对工件加热,工件的实时温度则又由红外测温仪采样后反馈至PLC形成温度闭环。系统运行过程的实时数据及现场设备的运行状态信息,均由相应的传感器件传送到PLC和工控机实施数据采集记录、报警提示等智能化控制,所有操作均可通过人机界面实现。

2 无超调PID温控设计
2.1 SIEMENS PLC中PID指令算法
在西门子PLC中,由于其PID算法是一种经典的PID算法,原理上与自动化仪表的控制思想是一致的。其PID控制结构如图2所示,输入输出关系为:

图2中,Sv(t)是输入量(给定值),Pv(t)是反馈量,C(t)为输出量。偏差值ev(t)=Sv(t)-Pv(t);mv(t)是PID调节器的输出信号。Kp是调节器的比例系数,Mintial是PID回路输出的初始值,PLC可编程控制器在对被控量PID调节时将PID公式离散化后,在系统的采样周期为Ts时,用矩形积分近似精确积分;用差分近似精确微分,将PID公式离散化,则第n次采样时控制器的输出为:
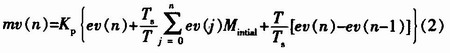

由于在实际的生产过程中要执行的温升曲线是图3(a)所示的工艺要求,Sv(t)输入量(给定值)在温升阶段期间。系统在采样周期Ts的作用下是按阶梯量的形式给定的,这就相当于每次给定的是一阶跃函数加n-1次的偏差值ev之和,因而,在实施PID做温度调节时出现温度超调振荡的现象是难免的,控制结果如图3(b)所示。因而,经典的PID控制结果是不能满足图3(a)的控制需求。
2.2 在实践中对该PID温控算法所做的设计改进
2.2.1 引入积分分离PID控制算法
积分分离PID控制算法是一种遇限消弱积分项的PID算法,对消除系统超调非常有效。其方法如下:根据实际调试情况,人为设定一阈值ε(ε>0);当偏差值|ev(n)|>ε时,采用PD控制,既可避免过大的超调又可使系统有较快的响应;当偏差值|ev(n)|≤ε时,采用正常的PID控制,以便保证系统的控制精度。这就需要在辨识决策环节中引入一积分项的控制系数β,β按下述条件取值。

引入积分项的控制系数β后,第n次采样时控制器的输出为:
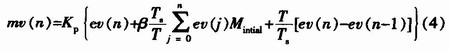
2.2.2 引入带死区的PID控制算法
在实际的控制系统中,采样周期Ts为100 ms。为避免控制动作的过于频繁而引起的振荡。引入了带死区的PID控制,其控制框图如图4所示。相应的控制算式为:
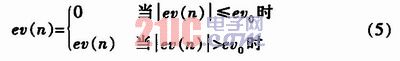
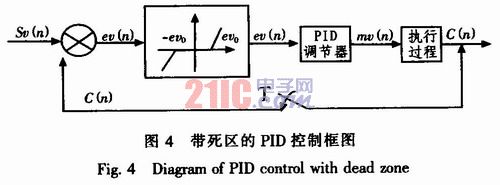
式中,死区evo是一个可调参数,其具体数值则根据实际调试情况而定,evo数值越小,控制动作越频繁,达不到稳定被控对象的目的;evo数值越大,则系统产生较大滞后,根据实际调试结果,在该温控系统中evo=2.0℃。
在引入死区控制的同时,本系统还设定了偏差值ev(n)大于某一上限定值ev(h)时则按比率认可ev(n)的数值,以此来限定由瞬间扰动产生的控制波动,此方法对保证系统控制的稳定性简洁有效。
2.2.3 引入微分先行的PID控制算法
微分先行的PID控制算法的特点是只对输出量C(n)进行微分,而对给定值Sv(n)不作微分,因而,在改变给定值时,输出稳定(微分项不参与)使被控量的变化比较缓和,这种输出量微分先行的控制算法非常适应与给定值频繁变化的场合,可以有效地抑制因给定值变化而引起的系统振荡。在本项目中,正是考虑到在温度上升阶段时在采样周期Ts的控制下每次的给定值都存在阶跃变化,因而引入微分先行的控制算法可明显改善系统的动态特性。微分先行的控制算式:

2.2.4 引入居里点温度检测的PID变参量控制算法
由于本系统的加热源采用的是电磁感应加热方式,在此方式下,当金属加热到居里点以上温度时,由于导磁率的急剧变化将使加热效率亦产生较大的变化,因此,在PID控制中,相应的比例参数Kp、积分参数Ki、和微分参数Kd也将随之相应的变动,变动量的大小根据加热工件的材质、尺寸、生产节拍均成函数关系。另一方面,为保证控制效果无超调并形成钝角的拐点,对系统的输出量mv(n)也需进行比例输出,本参数的变动量也是一与工件加热工艺关联的函数,其数值的优化需在调试中确定。
2.2.5 改进后的PID控制算法综述
根据本项目温控工艺要求的特点,在基于传统PID算法的理念下,经上述改进使该系统成为一具有一定自适应能力的系统,它能够识别环境条件的变化,并自动校正PID控制参量,这与传统的PID控制算法的显著区别在于它具有“辨识→决策→修改”的功能,即不间断地采样系统(被控对象)的阶段状态参数并加以辨识后与系统事先给定的准则相比较后实时决策、修改PID的算法,以使系统不断地趋向最理想的控制效果。改进后的PID算法的系统框图如图5所示。
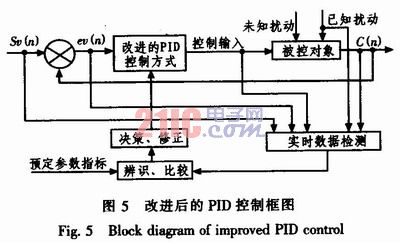
3 无超调PID温控设计性能指标
无超调PID温控设计的主要性能指标:从自控理论上讲,本系统的温控本质属于非线性系统,时域上的不确定因素复杂多变,判断其性能指标综合体现在以下几个通用的方面。
3.1 稳定性
稳定性是对控制系统的基本要求,按自适应PID控制算法系统的稳定性要求是指系统的状态、输入、输出和参数等变量在各种条件的变动下总是有界的,即控制算法的校正下,误差经闭环调节后有界收敛。本系统中,可编程控制器采用的是Siemens Smatic S7-200 PLC,系统中的相关变量均做过归一化处理,即数字量的引用均标准化在0.0~1.0之间,因而,在系统温控过程中是收敛有界的,同时,在对实时数据的检测、辨识、决策过程中,在程序内对所有参量均设有上下限的识别,从而有效保证了执行结果的稳定。
3.2 可维性
本系统的可维性主要指的是软件维护及操作者应用的便利程度,因在实际生产过程中,产品的规格、型号是多样化的,因而,在温控过程中与之相对应的PID参数亦需要相应的变动。在该系统中的人机界面中,通过控制组态,由操作者输入产品的规格编号后,在控制组态中自动调用配方数据来初始化PID的基础参数;另一方面,本系统的软件无论是组态编程还是PLC编程,均采用模块化结构,因而,系统程序的修改、维护极为便利。依照自控系统的一般规则,系统运行的过程数据均实时采集、记录到数据库中,可实时为产品生产加工质量的追溯提供源资料。
3.3 鲁棒性(Robust)
如前所述,本温控系统的被控对象是电磁感应加热源的功率输出,在实际的现场环境中,电磁场强的干扰及各类机电设备的运行对PID控制均存在种种已知或未知的扰动,解决此方面的问题除了在硬件上要采取相应的措施外,在PID温控的设计方面,通过应用上述各种参量限定辨识后,在实际的生产运行中均保证了系统的工作稳定,在相邻机电设备或变频电源的启停扰动下不敏感。
4 结论
4.1 无超调PID沮控实验效果
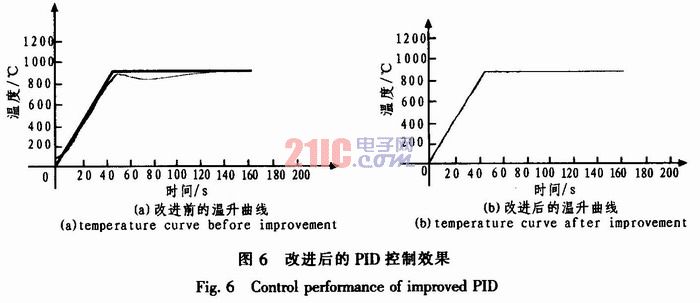
经上述改进后的PID控制算法在实际生产过程的运行中有效解决了原温控的难点,其控制效果如图6所示。图6(a)的曲线是采用改进PID温控算法前的温控曲线,图6(b)的温控曲线是本文所论述的PID算法所实时记录的温控效果,其中难得的是在变温拐点处的控制为理想的钝角,整体温控效果与预定的温度趋向基本吻合,在实际生产过程中与以往相比,既避免了因欠温而造成的返工现象,又消除了因过温产生的废品,有效地提高了产品热处理的质量。
4.2 无超调PID温控的设计结论
现代控制理论中,在经典PID控制理论的基础上衍生的控制理念层出不穷,诸如神经元、神经网络、模糊PID控制算法等比比皆是,但若要在生产实践中选取理想的控制算法,就必须通过工程实际进行反复地调整和修改,不拘泥于理论参数或方法限制,根据工程经验,直接在控制系统的试验中进行筛选组合出适合实际的控制算法,使系统达到最优化的运行状态。虽然在本项目的PID算法取得了预期的效果,但实际运行在各温度段的PID参数是在调试中获取,并针对各型号的产品规格在上位组态中以配方的形式给定,如此则使得前期调试颇为繁琐,因而,在参量自适应的智能化设计方面还有待于进一步的探索与实践。

